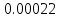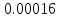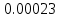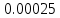Курсач на сдачу. Надежность вкр бакалавры Выполнил Агеев К. С
 Скачать 164.1 Kb. Скачать 164.1 Kb.
|
|
Надежность вкр бакалавры Выполнил Агеев К.С 10-406Б-17 Целью эксплуатационного раздела ВКР является овладение научными методами оценки и анализа надежности авиационной техники (АТ), получение навыков и умений применять теоретические знания к решению практических задач анализа надежности АТ.
2). Выполнить статистический анализ показателей безотказности невосстанавливаемых изделий ВС. 3). Выполнить статистический анализ показателей безотказности Исходные данные. Тип ЛА: Су-24 Изделие ГС: Гидроусилитель Тип изделия: КАУ-125 Количество изделий на самолёте: 2 Объём наблюдений: N =30*2 = 60 Статистические данные наработок до отказа («полные реализации»), (ч): 1050,1055,1110,1115,1210,1240,1370,1400,1520,1540,1570,1750,1820,1870,1950. Статистические данные наработок до цензурирования («неполные реализации»), (ч): m=m1+m2+m3=45 m1=16 по 1300 ч m2=18 по 1700 ч m3=11 по 2100 ч Анализ данных эксплуатационных наблюдений за отказами изделий СКВ парка ЛА. 1.1. Определение вида случайных величин наработки изделий (реализаций): наработки до отказа («полные реализации») и наработки до цензурирования («неполные реализации»). 1.2. Определение понятий: однократно цензурированные и многократно цензурированные выборки. 1.3. Построение ранжированных временных диаграмм (аналогов вариационных рядов) наработок до отказа ti где i = 1 ̅̅̅,̅𝑛̅ и наработок до цензурирования τj, где j = 1 ̅̅̅,̅𝑚̅̅. 1.4. Выбор размаха и числа интервалов временных диаграмм. Решение: 1.1.Статистические данные содержат два типа случайных величин (реализаций): наработки изделий, составляющих выборки: а) реализации, представляющие собой случайные величины наработок до отказа (между отказами) t1…,ti…,tn где i = 1 ̅̅̅,̅𝑛̅ Назовем их «полными реализациями»; б) реализации, представляющие собой величины наработок изделий до цензурирования τ1…, τj…, τm где j = 1 ̅̅̅,̅𝑚̅̅. Это соответствует случаю, когда испытания (наблюдения) прекращены или объект снят с испытаний до наступления отказа. Назовем их «неполными реализациями». 1.2. В первом случае используется полная выборка. Во втором случае имеет место цензурирование — событие, приводящее к прекращению эксплуатационных наблюдений изделий до наступления отказа (предельного состояния). При формировании выборки изделий во втором случае образуется цензурированная выборка, элементами которой являются значения наработок до отказа (полные реализации) и наработок до цензурирования (неполные реализации). Различаются однократно и многократно цензурированные выборки. В однократно цензурированной выборке значения всех наработок до цензурирования равны между собой и меньше наибольшей наработки до отказа. Многократно цензурированная выборка характеризуется значениями наработок до цензурирования, не равными между собой. 1.3. По исходным данным построим ранжированные временные диаграммы наработок до отказа ti где i = 1 ̅̅̅,̅𝑛̅ (n = 15) и наработок до цензурирования τj, где j = 1 ̅̅̅,̅𝑚̅̅ (m = 45). Результаты представлены на рис. 1 и 2. При этом реализации расположим в следующем порядке: сначала «полные реализации» в порядке возрастания, затем «неполные реализации» в порядке убывания 1.4. Сгруппируем результаты наблюдений. При этом размах выборки ν = 2100 (ч), а число интервалов L = 4 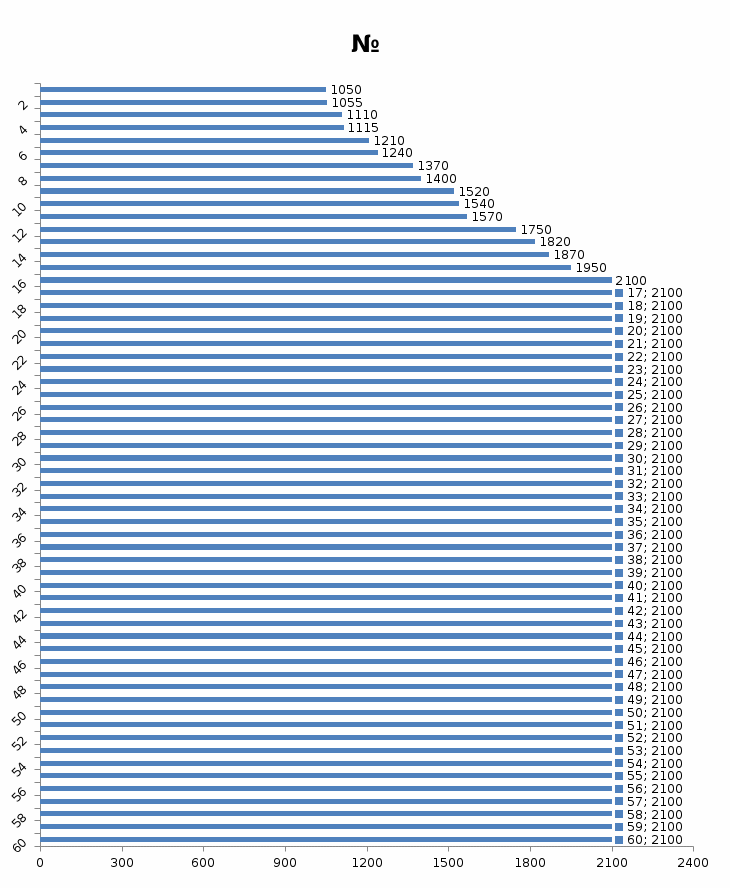 Рис.1 Ранжированная временная диаграмма наработок до отказа и до цензурирования (однократно цензурированная выборка)  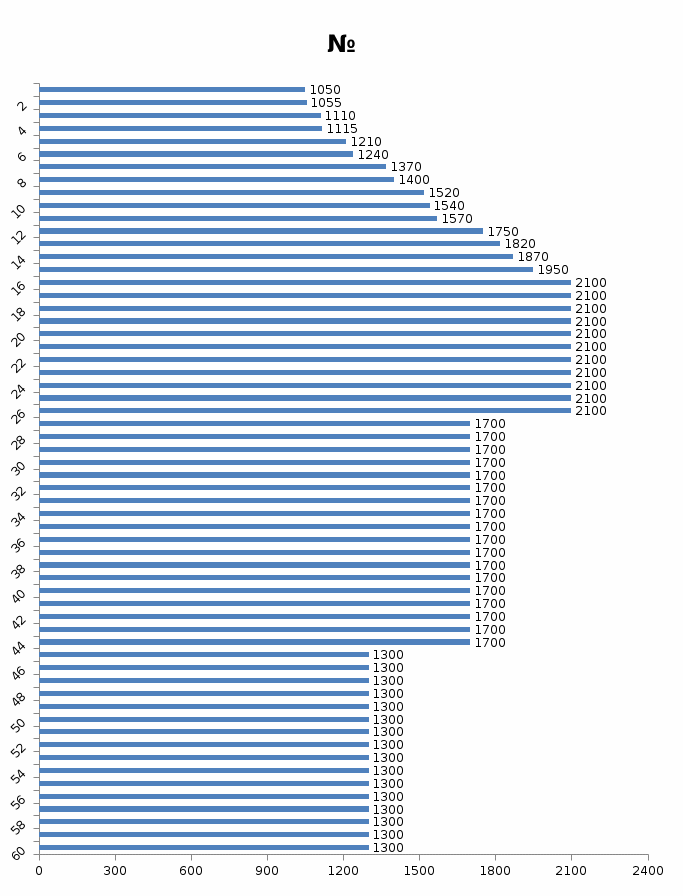 Рис.2 Ранжированная временная диаграмма наработок до отказа и до цензурирования (многократно цензурированная выборка) Задача № 2. Статистический анализ показателей безотказности невосстанавливаемых изделий ЛА параметрическим методом. 2.1. Классификация и выбор методов оценки показателей безотказности изделий. 2.2. Оценка показателей безотказности параметрическим методом для однократно цензурированной выборки. а) оценка и построение гистограмм статистической плотности распределения f*(t) и статистической интенсивности отказов λ*(t); б) формирование гипотезы о законе распределения для однократно цензурированной выборки; Решение: 2.1. Анализ методов оценки показателей надежности изделий. Параметрический метод оценки показателей надежности предусматривает при известном законе распределения наработки до отказа и других случайных величин выполнение следующих операций: - оценку параметров закона распределения, входящих в расчетную формулу определенного показателя надежности, - оценку показателей надежности по вычисленным оценкам параметров закона распределения. При неизвестном законе распределения определяется сначала закон распределения. Непараметрический метод предусматривает при неизвестном законе распределения наработки до отказа выполнение непосредственной оценки показателей надежности по данным эксплуатационных наблюдений. 2.2. Задача оценки показателей безотказности параметрическим методом заключается в следующем. По данным наблюдений известны наработки τ1, τ2,..., τi…, τn,(N-n)*T , где T ≥ τn, т.е. для (N-n) изделий наработка до отказа будет больше некоторого значения Т, определяющего период эксплуатационных наблюдений. Данная совокупность статистических данных характеризуется переменностью парка изделий в различных интервалах наработки и усеченностью выборки. Ранжированная временная диаграмма для однократно цензурированной выборки представлена на рисунке 1 задачи №1. а) Оценка статистической плотности распределения f*(t) и интенсивности отказов λ*(t) производится для каждого интервала ∆ti по формулам: 𝑓𝑡∗ = ∆𝑛𝑖 𝑁𝑖×∆𝑡𝑖 𝜆∗𝑡 = ∆𝑛𝑖 [𝑁𝑖-𝑛𝑖(𝑡)]×∆𝑡𝑖 ; где: где: ∆𝑛𝑖—число отказавших изделий в интервале ∆𝑡𝑖; Ni — число изделий, наблюдаемых в интервале ∆𝑡𝑖; 𝑛𝑖(𝑡) — число отказавших изделий до начала i-ro интервала. Число Ni для i-ro интервала определяется как общее число всех реализаций диаграммы за исключением тех неполных реализаций, которые по величине меньше левой границы этого интервала: Ni = N - ∑𝑗 𝑗- =1 1 𝑚𝑗 Расчёт для интервала (900 ÷ 1200) 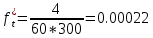 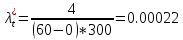 Расчёт для интервала (1200 ÷ 1500) 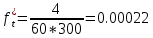 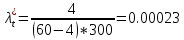 Расчёт для интервала (1500 ÷ 1800) 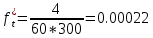 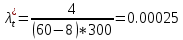 Расчёт для интервала (1800 ÷ 2100) 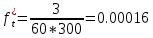 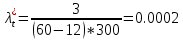 Результаты расчётов представлены в таблице 1. Таблица 1
По результатам расчётов строим гистограммы статистической оценки плотности распределения f*(t) и интенсивности отказов λ*(t), представленные на рисунках 3 и 4. 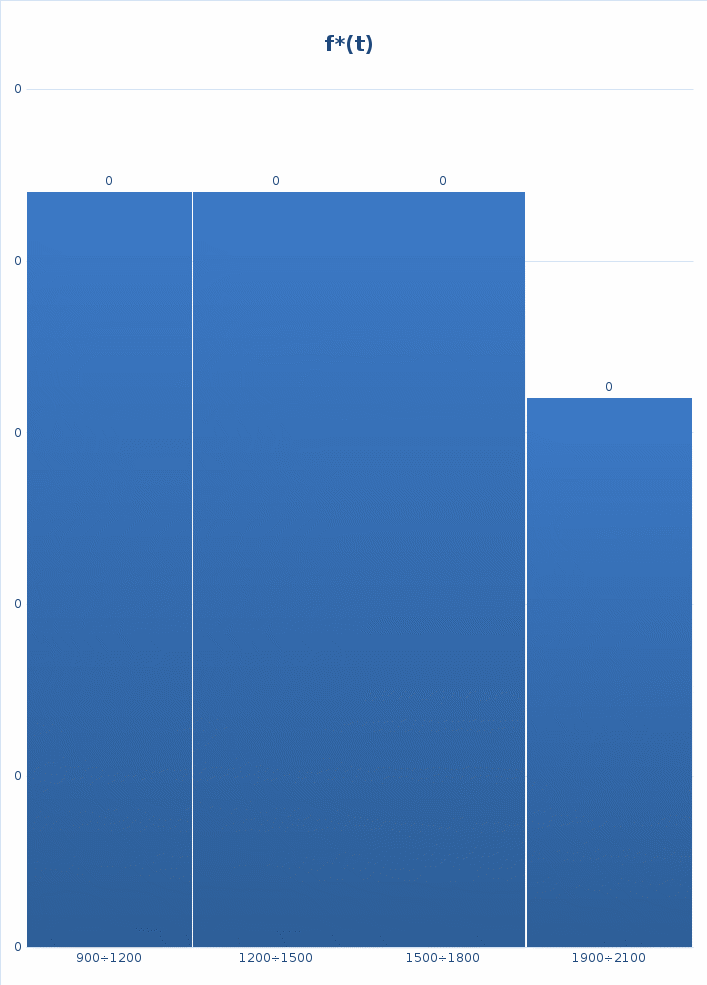 Рис 3. Гистограмма статистической оценки плотности распределения f*(t). 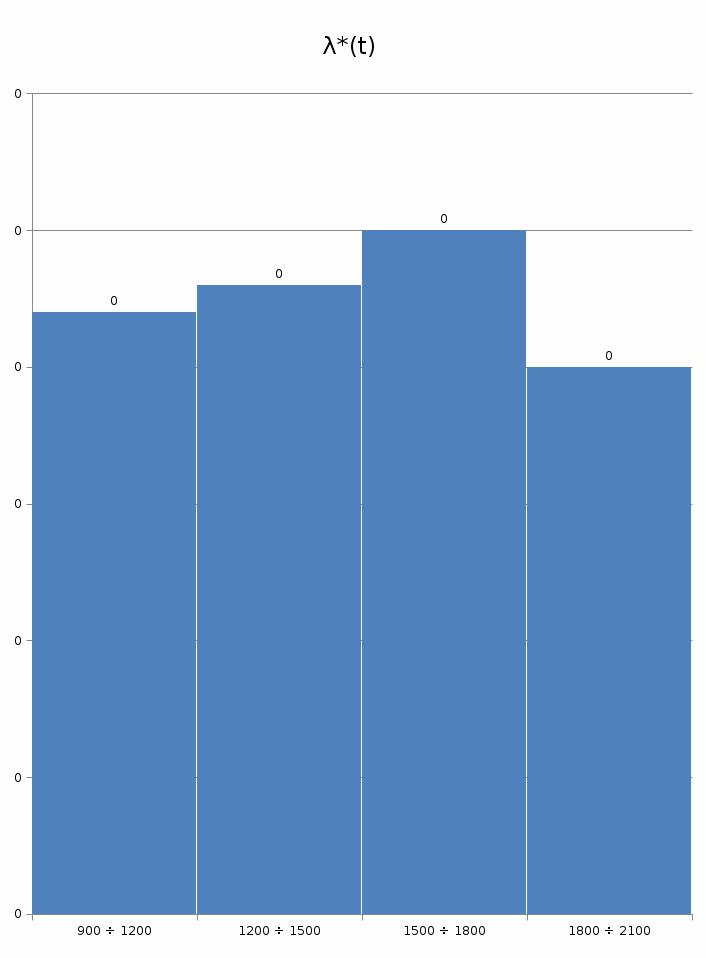 Рис 4. Гистограмма статистической оценки интенсивности отказов λ*(t) б) Сравнительный анализ гистограмм f*(t) и λ*(t) с теоретическими кривыми f(t) и λ(t) позволяет выдвинуть гипотезу о распределении наработки до отказа по закону Вейбулла. 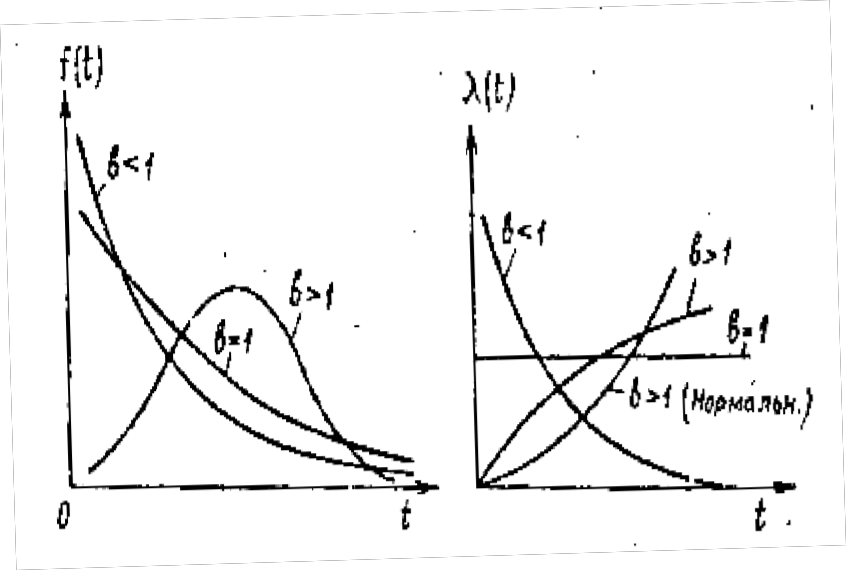 Рис.5 Теоретические зависимости f(t), λ(t) для различных законов Рис.5 Теоретические зависимости f(t), λ(t) для различных законовраспределения: экспоненциального (b=1), нормального (b>1), Вейбулла (b<1, b>1) |