РГР матанализ. Задача Провести процесс ортогонализации системы функций 1 в 2 в Решение Имеем набор функций

• Название: Задача Провести процесс ортогонализации системы функций 1 в 2 в Решение Имеем набор функций
• Анкор: РГР матанализ
• Дата: 07.12.2020
• Размер: 220.5 Kb.
• Имя файла: РГР матанализ.doc
• Тип: Задача; #157874

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ

Федеральное государственное бюджетное

Образовательное учреждение высшего образования

«Тверской государственный университет»

Факультет прикладной математики и кибернетики

Направление 01.03.02 Прикладная математика и информатика

Профиль подготовки: «Математическое моделирование»

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

По дисциплине «Математический анализ»

Автор: студент 2 курса 24гр.

Скакодуб Давид Романович
Проверил:

Малышкин Юрий Андреевич

Тверь­ – 2020

Вариант 20.
Задача 1. Провести процесс ортогонализации системы функций
1) в ;
2) в ;
Решение:

1. 
   Имеем набор функций
   

.
Выполним процесс ортогонализации Грама – Шмидта.
Положим первую функцию .
Вторую функцию ищем по формуле:
.
Вычислим скалярные произведения функций в заданном пространстве:


,



.
Таким образом,
.
Третью функцию найдем по формуле:
.
Вычисляем необходимые скалярные произведения:




,



,



.
Таким образом, третья функция равна


.
Четвертую функцию ищем по формуле:
.
Вычислим необходимые скалярные произведения:



,



,



,





.
Четвертая функция равна


.
Получили искомый ортогональный набор функций:
.

2. 
   
   

Решение:
Имеем набор трех различных функций:
.
В качестве первой функции берем .
Вторую функцию ищем по формуле: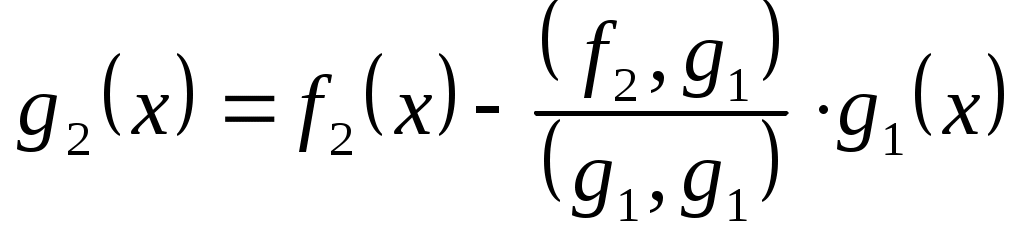
.
Вычислим скалярные произведения функций в заданном пространстве: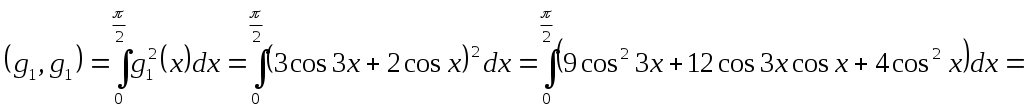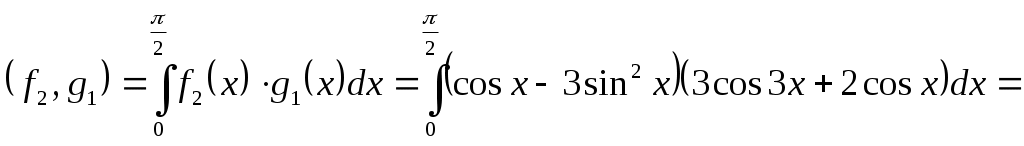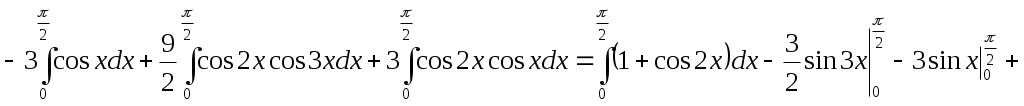


,









.

Таким образом,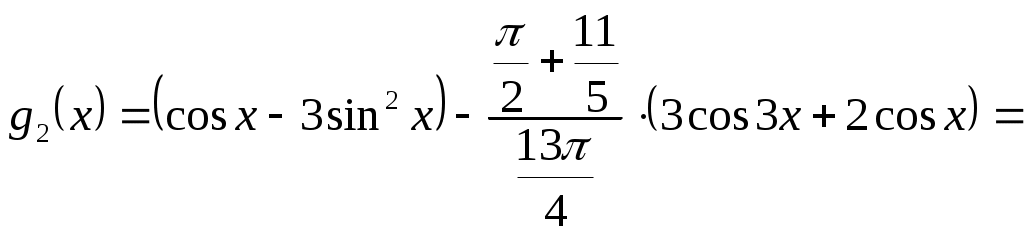



.
Третью функцию найдем по формуле:
.
Вычисляем необходимые скалярные произведения: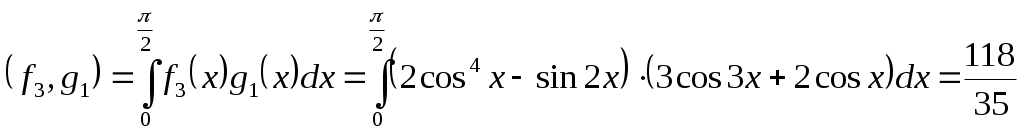



,

,

.
Таким образом, третья функция равна






.
Получили искомый ортогональный набор функций:
.

Задача 2. Разложить в ряд Фурье в интервале функцию .
Решение:
Искомый ряд Фурье на заданном интервале:
.
Вычислим коэффициенты Фурье: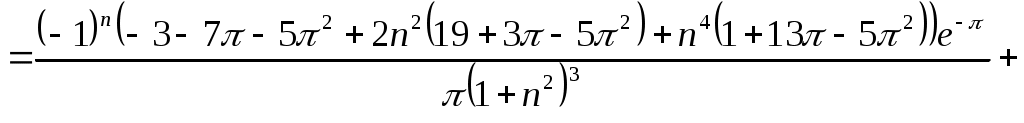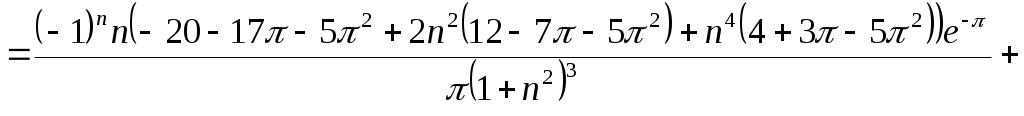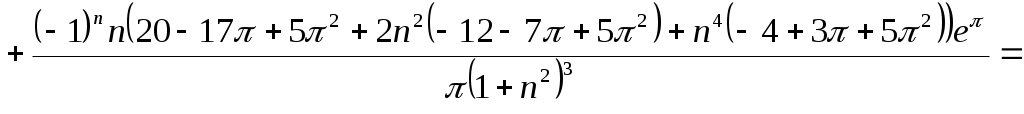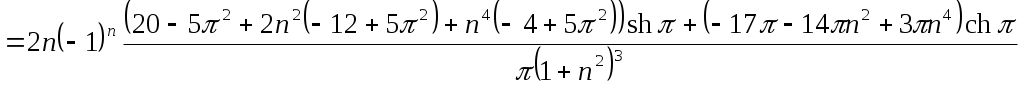










,







,






.
Искомый ряд Фурье:




.