сопромат. Задача 2.1+. Задача Расчет балки на прочность
 Скачать 347.64 Kb. Скачать 347.64 Kb.
|
|
Задача 2.1. Расчет балки на прочность. Для расчетной схемы с указанными размерами и нагрузками построить по длине балки эпюры изгибающих моментов Мх и поперечных сил Qx. Подобрать поперечное сечение балки из условия прочности: - прямоугольного профиля, полагая, что балка деревянная при 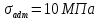 ; соотношение между размерами сечения принять равным b:h=1:2; ; соотношение между размерами сечения принять равным b:h=1:2;- двутаврового профиля, материал сталь при 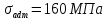 , , 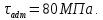 - проверить стальную балку (двутавр) на прочность: а) по рабочим нормальным напряжениям, б) по максимальным касательным напряжениям. Исходные данные: схема – 7; a1=0,1 м; a2=0,5 м; a3=0,2 м; l=1 м; М=44кН·м; q=15кН/м; Решение: 1. Расчёт балки следует начинать с расстановки и определения величины опорных реакций. Величина и направление опорных реакций и реактивных моментов могут быть определены из решения уравнений равновесия. Для плоской системы параллельных сил (поперечный плоский изгиб) условия равновесия описываются двумя уравнениями статики: 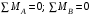 . .Рассматриваемая балка имеет две шарнирные опоры.В опоре А возникает одна реакция RA, в опоре В направление реакции в общем случае неизвестно, поэтому разложим её на две составляющие: НB и RB. Все нагрузки действуют перпендикулярно продольной оси балки, поэтому из уравнения проекций на горизонтальную ось х получается, что составляющая НB=0. Запишем уравнения моментов сил относительно опоры А 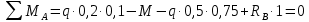 Отсюда 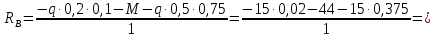 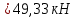 Запишем уравнения моментов сил относительно опорыB 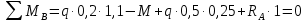 Отсюда 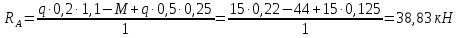 Для проверки правильности вычисления опорных реакций составим уравнение проекций всех сил на вертикальную ось у: 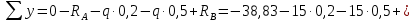 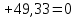 Последнее уравнение обращается в тождество, следовательно, величина реакций и их направление определены правильно. 2. Для изгибающих моментов и поперечных сил разобьём балку на участки. Участки пронумеруем слева-направо. Рассчитываемая балка имеет четыре участка I – IV. При составлении аналитических выражений для 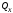 и и 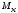 в пределах I-го участка проведём сечение с абсциссой в пределах I-го участка проведём сечение с абсциссой 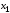 и рассмотрим равновесие левой части консоли. На эту часть балки действует нагрузка q=15 кН/м, поэтому поперечная сила QI= -q·x1, а изгибающий момент MI= -q·x1·x1/2. и рассмотрим равновесие левой части консоли. На эту часть балки действует нагрузка q=15 кН/м, поэтому поперечная сила QI= -q·x1, а изгибающий момент MI= -q·x1·x1/2.Вычислим ординаты в начале и в конце участка: при х1 = 0 QI= 0, MI= 0. при х1 = 0,2 м QI= - q·0,2= - 3 кН, MI= - q·0,2·0,1= - 0,3 кН·м. Для составления аналитических выражений 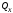 и и 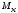 в пределах II-го участка проводим сечение с абсциссой в пределах II-го участка проводим сечение с абсциссой 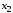 и рассматриваем равновесие левой части балки. и рассматриваем равновесие левой части балки.QII= -q·0,2 - RA= -41,83 кН − поперечная сила в пределах II-го участка постоянна. MII= -q·0,2(0,1+x2) -RA·x2. Это уравнение прямой линии, для её построения достаточно определить ординаты изгибающего момента в двух точках (на концах участка): при х2 = 0 MII= - q·0,2·0,1= - 0,3 кН·м, при х2 = 0,1 м MII= -q·0,2·0,2 -RA·0,1= - 4,48 кН·м. Для III-го участка (сечение с абсциссой 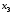 ) )QIII= -RB+q·0,5= -49,33+15·0,5= - 41,83 кН − поперечная сила в пределах III-го участка постоянна. MIII=RB·(0,5+x3) -q·0,5 (0,25+x3). Это уравнение параболы. Для её построения определяем моменты: при х3 = 0 MIII=RB·0,5 -q·0,5 0,25=22,79 кН·м. при х3 = 0,4 м MIII=RB·0,9 -q·0,5·0,65=39,52 кН·м. Для IV-го участка (сечение с абсциссой 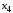 ) поперечная сила равна: ) поперечная сила равна:QIV= - RB+qx4. - прямая линия. MIV=RB·x4 - q·x3·x3/2. - это уравнение параболы. Вычислим ординаты в начале и в конце участка: при х4= 0 QIV= - RB= - 49,33 кН, MIV=0; при х4 = 0,5 м QIV= - RB+q·0,5= - 41,83 кН, MIV=RB·0,5 -q·0,5·0,25=22,79 кН·м При построении эпюр Qx и Мxвыбираем масштаб и откладываем положительные значения ординат эпюр от нулевой линии вверх, а отрицательные вниз. После построения эпюр устанавливаем наибольшие значения (по абсолютной величине) поперечной силы Qmax=49,33 кН и изгибающего момента 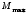 =39,52 кН·м. =39,52 кН·м.Сечение С является «опасным», в нем Qx=41,83 кН и изгибающий момент 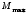 =39,52 кН·м кН·м. =39,52 кН·м кН·м.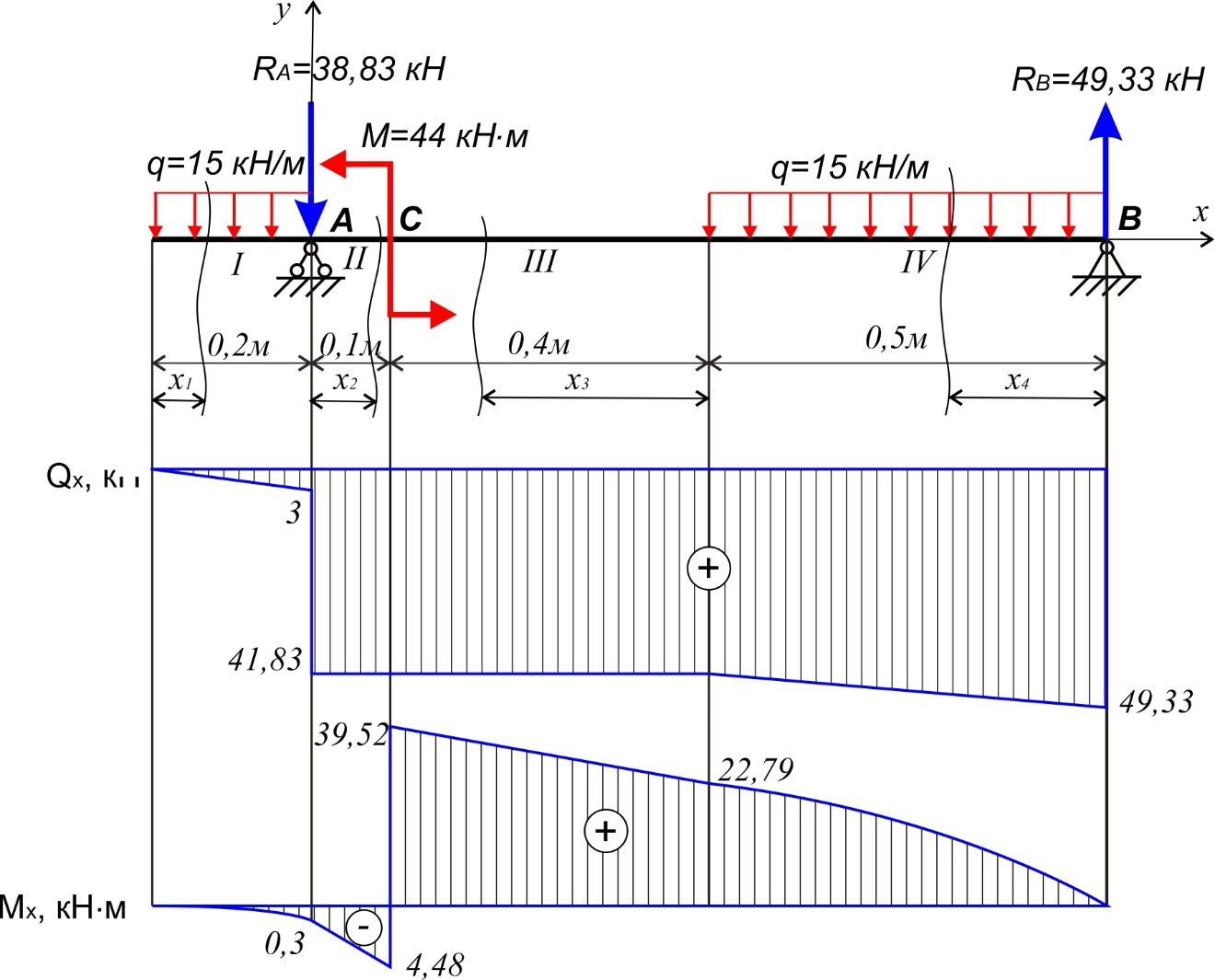 3. Подбор поперечного сечения балки проводим в соответствии с условием задания в двух вариантах: а) подбор сечения прямоугольного профиля деревянной балки: 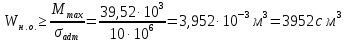 для прямоугольного сечения (при h/b=2) 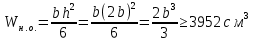 Тогда 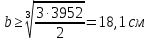 Принимаем b=20 cм, h=40 см. б) подбор сечения двутаврового профиля: 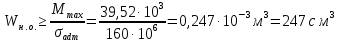 Из таблицы сортамента проката этому значению соответствует двутавр № 22а, для которого Wн.о.=Wx=254 см3. Основные размеры и геометрические характеристики профиля: высота h=220 мм; толщина стенки d=5,4·мм; момент инерции сечения относительно нейтральной оси Iн.о.=Ix=2790 см4; статический момент половины площади сечения относительно нейтральной оси Sн.о.=Sx=143 см3. 4. Проверка стальной балки на прочность: а) проверка по рабочим нормальным напряжениям 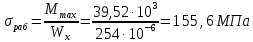 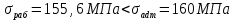 т. е. условие прочности выполняется. б) проверка по максимальным касательным напряжениям (формула Д.И. Журавского): 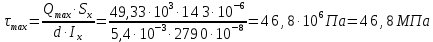 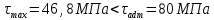 Таким образом, условие прочности выполняется. 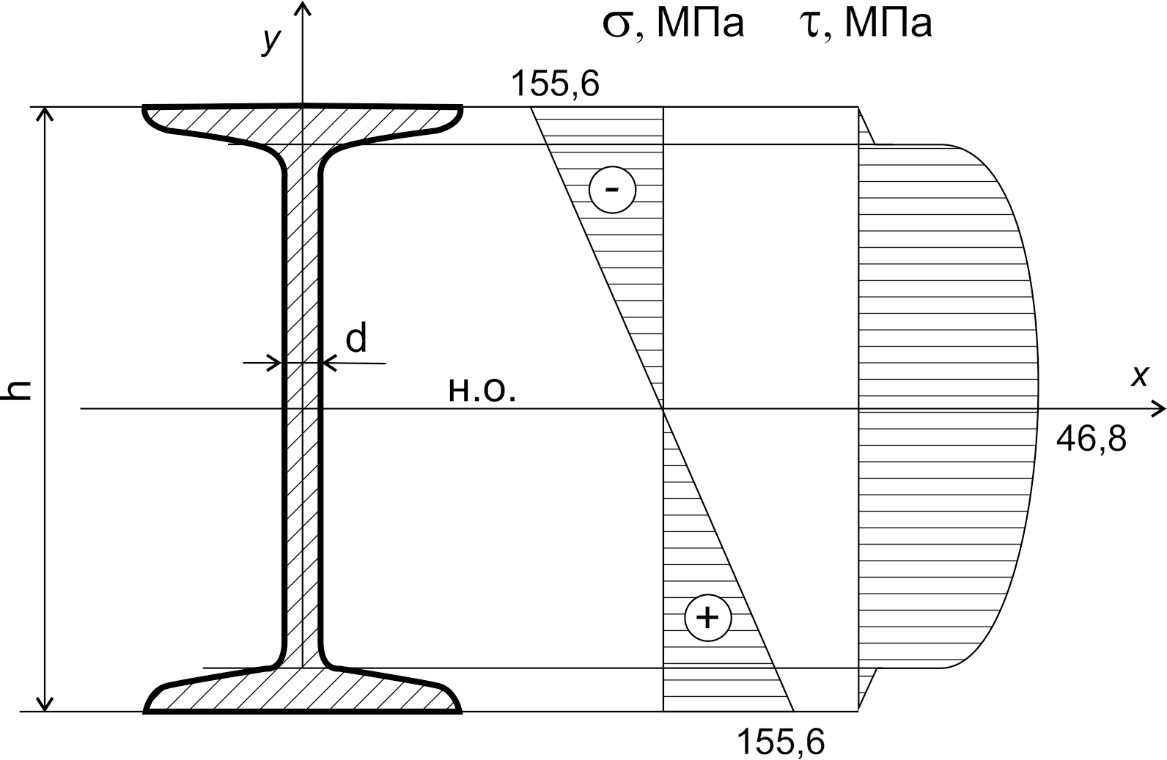 |
