папав. задание 23.03.20. Задача Расчет динамических характеристик линейных сау
 Скачать 40.6 Kb. Скачать 40.6 Kb.
|
|
Задача 1. Расчет динамических характеристик линейных САУ Определить весовую функцию g(t) и переходную функцию h(t) линейной САУ, состоящей из последовательного соединения апериодического и идеального интегрирующего звеньев, по заданным в табл. 1 параметрам ее передаточной функции в соответствии с последними двумя цифрами учебного шифра: 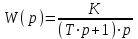 , где р - оператор Лапласа. , где р - оператор Лапласа.Составить таблицу расчетных значений искомых временных характеристик и построить их графики для временного интервала: t = 0 - 5T с шагом дискретизации, равным 0,5Т. Масштаб по оси ординат студентом выбирается самостоятельно, исходя из того, что высота графика должна быть не менее 8-10 см. Таблица 1
Пример. В качестве примера рассмотрим САУ, передаточная функция которой имеет следующий вид: 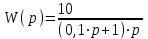 . .Известно, что изображение весовой функции L[g(t)] любой линейной САУ есть ничто иное, как ее передаточная функция: L[g(t)] = 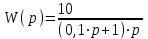 . .Для отыскания оригинала весовой функции g(t) = L-1[W(p)] разложим W(p) на элементарные дроби, соответствующие передаточным функциям отдельных звеньев системы САУ, и воспользуемся методом неопределенных коэффициентов для определения неизвестных статических коэффициентов усиления этих звеньев (коэффициенты А и В в знаменателе элементарных дробей): 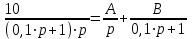 . (1) . (1)После приведения правой части выражения (1) к общему знаменателю можно приравнять числители левой и правой частей полученного уравнения: 10 = А∙(0,1∙р + 1) + В∙р = р∙(0,1∙А + В) + А (2) Приравнивая коэффициенты левой и правой частей уравнения (2) при одинаковых степенях р, получим систему двух уравнений из двух неизвестных: = А; = 0,1∙А + В, откуда А= 10; В = - 0,1∙А = - 1. Подставляя вычисленные значения коэффициентов А и В в уравнение (1), получим: 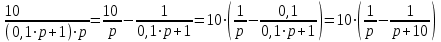 . (3) . (3)Переход от изображений элементарных функций f(p) в операторной форме записи к их оригиналам, как функций времени f(t), осуществляется, как правило, с использованием стандартных таблиц изображений, приводимых в справочной литературе. Так, например: оригинал L-1[1/р] функции 1/р равен: L-1[1/р] = 1. оригинал L-1[1/(р + 10)] функции 1/(р + 10) равен:L-1[1/(р + 10)] = е -10∙t. Заменив в правой части уравнения (3) изображения элементарных функций на их оригиналы, получим искомое выражение для весовой функции: g(t) = 10∙(1 - е -10∙t) (4) Задаваясь различными значениями t, заполним таблицу расчетных значений и построим график g(t). По известной весовой функции g(t) можно найти переходную функцию h(t), принимая во внимание, что h(t) = 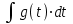 . .Изображение L[h(t)] функции h(t) можно получить путем умножения передаточной функции W(p) исходной САУ на передаточную функцию 1/р идеального интегрирующего звена, что соответствует включению последовательно с САУ интегрирующего звена. L[h(t)] = W(p)∙1/р = 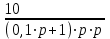 . 5) . 5)Разложим правую часть уравнения (5) на элементарные дроби с тем, чтобы получить более простые изображения функций для нахождения их оригиналов. 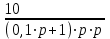 = = 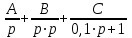 . (6) . (6)После приведения правой части выражения (6) к общему знаменателю приравняем числители левой и правой частей полученного уравнения: 10 = А∙р∙(0,1∙р +1) + В∙(0,1∙р + 1) + С∙р2. (7) Приравнивая коэффициенты левой и правой частей уравнения (7) при одинаковых степенях р, получим систему трех уравнений из трех неизвестных: 10 = В; = 0,1∙В + А; = 0,1∙А + С, откуда В= 10; А = - 0,1∙В = - 1; С = - 0,1∙А = 0,1. Подставляя вычисленные значения коэффициентов А, В и С в уравнение (6), получим: 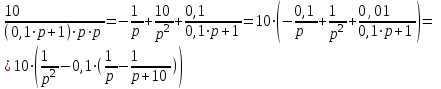 . (8) . (8) Воспользовавшись известными таблицами изображений, найдем оригиналы простейших функций: L-1[1/р] = 1; L-1[1/р2] = t; L-1[1/(р + 10)] = е -10∙t. Заменив в правой части уравнения (8) изображения элементарных функций на их оригиналы, получим искомое выражение для переходной функции: h(t) = 10∙[t - 0,1∙(1 - е -10∙t)] (9) Задаваясь различными значениями t, заполним таблицу расчетных значений и построим график h(t). Этот результат можно получить путем непосредственного интегрирования весовой функции g(t): h(t) = 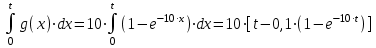 | ||||||||||||||||||||||||||||||||||||
