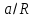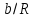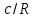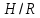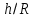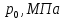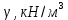Пояснительная записка Курсовой проект по строительной механике. Задача Расчеты на прочность и жесткость круглых пластин при осесимметричном изгибе
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
Задача 2. Расчет на прочность оболочки вращения при осесимметричном нагруженииПостановка задачи: Произвести расчет на прочность нагруженной составной осесимметричной оболочки вращения. Таблица 3  Исходные данные. Исходные данные.
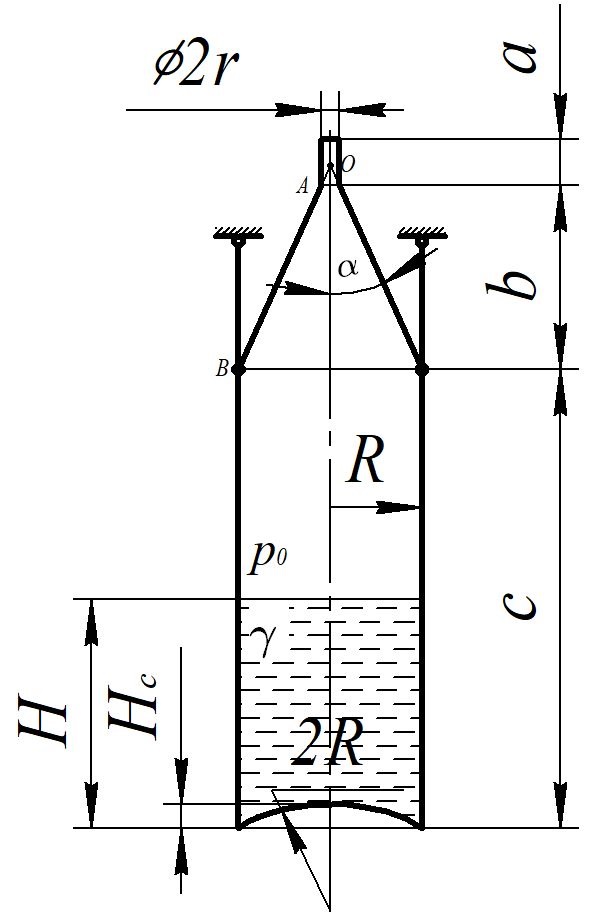  Рисунок 15  Расчетная схема оболочки. Расчетная схема оболочки.Дано: расчетная схема 4 (рисунок 17); геометрические размеры: 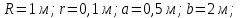 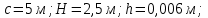 действующие нагрузки: удельный вес жидкости  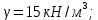 давление газа давление газа 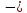 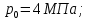 материал: сталь 25ХГС, предел текучести 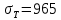 МПа, предел прочности МПа, предел прочности 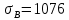 МПа. МПа.Требуется: построить эпюры давления 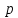 , кольцевых , кольцевых 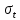 , меридиональных , меридиональных 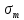 и эквивалентных (по третьей гипотезе прочности напряжений); и эквивалентных (по третьей гипотезе прочности напряжений);определить запас прочности нагруженной оболочки. Решение: Резервуар является составной оболочкой и состоит из конических и цилиндрических частей. Верхняя цилиндрическая часть резервуара: кольцевое напряжение: 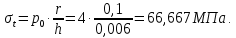 меридиональное напряжение: 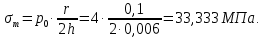 Коническая часть резервуара: угол полураствора конуса: 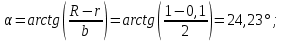 кольцевое напряжение и меридиональное напряжение: 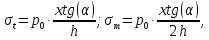 где 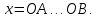 Из геометрических соотношений: 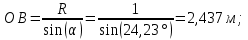 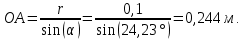 Значения напряжений при 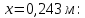 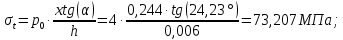 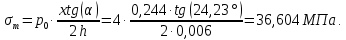 Значения напряжений при 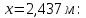 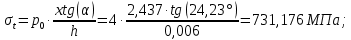 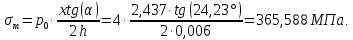 Цилиндрическая часть над зеркалом жидкости: кольцевое напряжение: 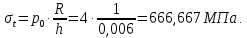 меридиональное напряжение: 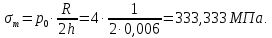 Цилиндрическая часть, заполненная жидкостью: кольцевое напряжение и меридиональное напряжение: 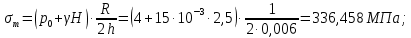 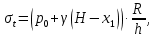 где 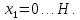 Значение напряжения при 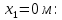 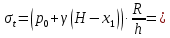 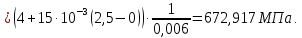 Значение напряжения при 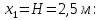 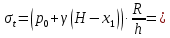 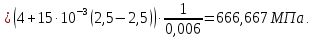 Сферическая часть: напряжения: 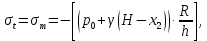 где 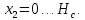 Из геометрических соотношений: 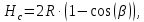 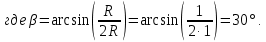 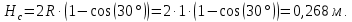 Значение напряжения при 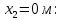 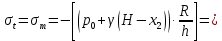 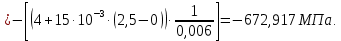 Значение напряжения при 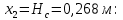 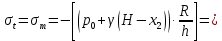 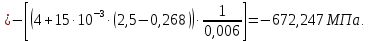 Давление в нижней точке: 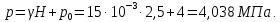 По третьей гипотезе прочности имеем: где 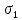 , , 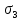 – главные напряжения. – главные напряжения.В рассматриваемом резервуаре напряжение 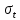 и и 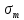 являются главными, причем являются главными, причем 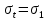 , , 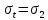 , , 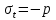 . .Так как 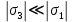 , то , то 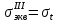 , эпюра , эпюра 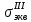 совпадает с эпюрой совпадает с эпюрой 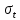 . .Запас прочности: 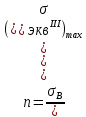 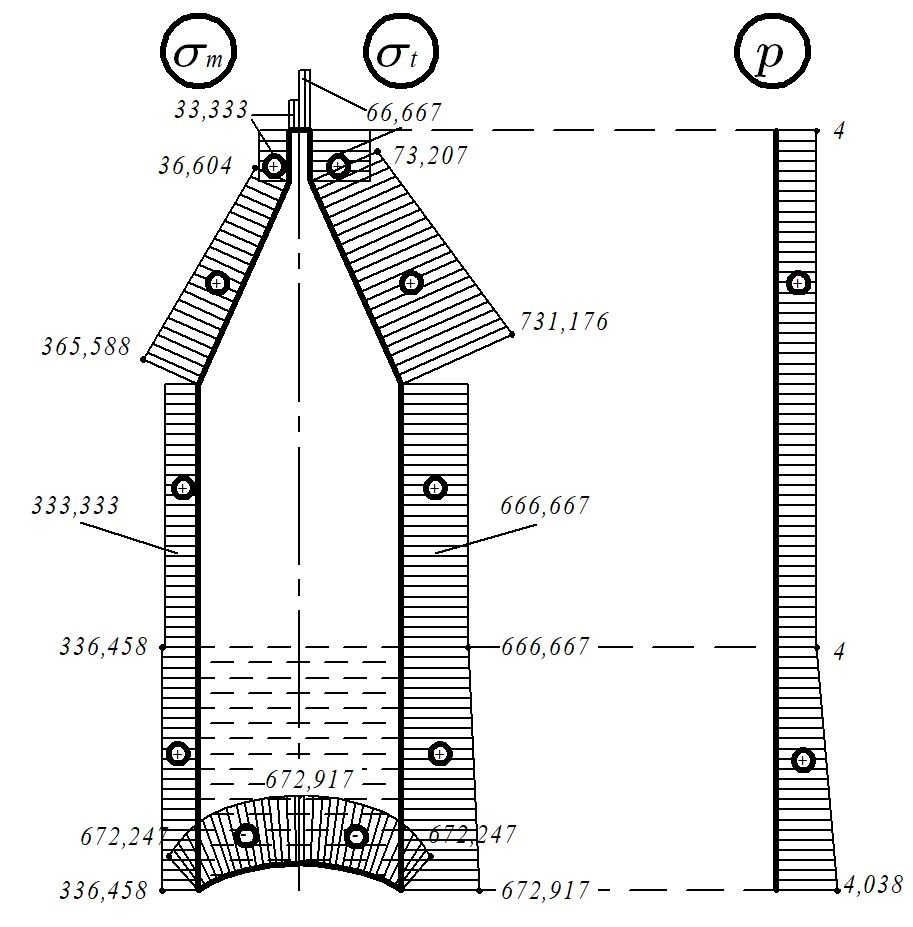  Рисунок 16 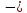 Эпюры напряжений и прикладываемого давления. Эпюры напряжений и прикладываемого давления.Выводы и результаты: построены эпюры давления 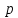 , кольцевых , кольцевых 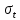 , меридиональных , меридиональных 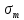 и эквивалентных и эквивалентных 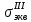 (по третье гипотезе прочности) напряжений. Кольцевые напряжения больше в 2 раза чем меридиональные во всех частях оболочки вращения (кроме сферической части, для сферической части (по третье гипотезе прочности) напряжений. Кольцевые напряжения больше в 2 раза чем меридиональные во всех частях оболочки вращения (кроме сферической части, для сферической части 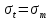 ), и имеют максимальное значение в донной части резервуара. ), и имеют максимальное значение в донной части резервуара.значения кольцевых 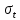 и меридиональных и меридиональных 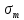 прямо пропорциональны радиусу и обратно пропорциональны толщине стенки. При определении кольцевых прямо пропорциональны радиусу и обратно пропорциональны толщине стенки. При определении кольцевых 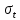 и меридиональных и меридиональных 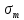 оболочки вращения формы усеченного конуса можно заметить, что при увеличении угла полураствора значения возникающих внутренних напряжений будут уменьшаться. оболочки вращения формы усеченного конуса можно заметить, что при увеличении угла полураствора значения возникающих внутренних напряжений будут уменьшаться.определили, что резервуар не разрушается под данной нагрузкой, т.к. запас прочности 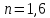 . Есть смысл провести испытание на разрушения конструкции, для выявления пределов прочности и текучести материала, также следует усилить бак внутренними или внешними силовыми наборами; . Есть смысл провести испытание на разрушения конструкции, для выявления пределов прочности и текучести материала, также следует усилить бак внутренними или внешними силовыми наборами;Данный метод расчета можно использовать для таких элементов конструкции ракеты, как топливные баки (нагруженные внутренним давлением и гидростатической нагрузкой), корпуса ракеты (нагруженные внешними нагрузками), также данную методику можно использовать для расчета баллонов, заполненных жидкостью или газом. ЗаключениеВ ходе курсовой работы были решены следующие задачи: Расчет на прочность и жесткость круглой стальной пластины при осесимметричном изгибе; Расчет на прочность нагруженной составной осесимметричной оболочки вращения; По каждой задаче представлены выводы, исходя из полученных результатов. |