Контрольная работа по прикладной механике. ПрикладнаяМеханика. Задача Равновесие тела под действием плоской системы сил На горизонтальную балку пролетом
 Скачать 155.39 Kb. Скачать 155.39 Kb.
|
|
Задача 1. Равновесие тела под действием плоской системы сил На горизонтальную балку пролетом AB=l действует сосредоточенная сила 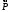 , пара сил с моментом M и равномерно распределённая нагрузка интенсивностью q. Определить реакции опор в точках A и B, пренебрегая весом балки и стержня BC. Схемы к задаче приведены на рис. 1, численные данные в табл.1. , пара сил с моментом M и равномерно распределённая нагрузка интенсивностью q. Определить реакции опор в точках A и B, пренебрегая весом балки и стержня BC. Схемы к задаче приведены на рис. 1, численные данные в табл.1. Рисунок 1. Схема к задаче l=2м; 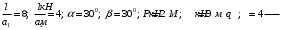 Решение Задача 1 относится к равновесию тела (балки) под действием плоской системы сил. Для определения реакций опор необходимо составить три уравнения равновесия для балки, приложив к ней активные (заданные) силы и силы реакций связей (опорные реакции). При вычислении момента силы 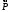 относительно выбранной точки иногда бывает удобно разложить эту силу на две составляющие и найти момент силы относительно выбранной точки иногда бывает удобно разложить эту силу на две составляющие и найти момент силы 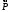 как сумму моментов этих составляющих. Распределенная нагрузка, приходящаяся на единицу длины, называется интенсивностью нагрузки и обозначается обычно буквой q. Равнодействующая распределенной нагрузки равна грузовой площади (площади эпюры нагрузки) и приложена в центре тяжести этой площади. как сумму моментов этих составляющих. Распределенная нагрузка, приходящаяся на единицу длины, называется интенсивностью нагрузки и обозначается обычно буквой q. Равнодействующая распределенной нагрузки равна грузовой площади (площади эпюры нагрузки) и приложена в центре тяжести этой площади.Определим характерные размеры:  ; ;  2. Заменим действующие на балку распределенные нагрузки равнодействующими силами 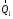 и и , приложенными к серединам участков распределения (рис. 2): , приложенными к серединам участков распределения (рис. 2): 3. Отбросим действующие на балку связи и заменим их соответствующими силами реакций. В точке А шарнирно-неподвижную опору заменяем реакцией, которую раскладываем на две составляющих  и и  ; стержень ВС заменяем реакцией стержня ; стержень ВС заменяем реакцией стержня 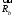 , направленной по стержню. , направленной по стержню.y 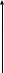 Ray Q1 P B 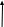 Rax    M A  x        a2 Rb a1/2   a1  l 4. Для полученной системы сил составляем уравнения равновесия. 1) 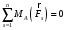 2) 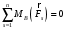 3)  Записывая эти условия для данной задачи, получим три уравнения, которые содержат по одной неизвестной. Решаем их. 1) 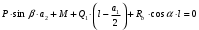 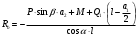 ; ; 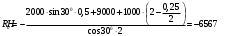 2)   5337Н 5337Н3)   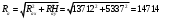 Проверка 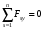  Задача 2. Определение центра тяжести плоской фигуры. Определить положение центра тяжести плоской фигуры. Схемы к задаче приведены на рис. 2, численные данные в табл. 2.  a=20 см b=10 см Решение 
 ; ;  Ответ: xc=3,52 см; yc=7,2 см Задача 3. Плоскопараллельное движение твердого тела Кривошип ОА=r вращается вокруг оси О с постоянной угловой скоростью и приводит в движение шатун АВ=l и ползун В. Для заданного положения механизма найти скорость и ускорение ползуна В. Примечание. Если данные таковы, что шатун окажется перпендикулярным направляющей ползуна (схемы I, VI), то вместо заданного угла следует принять =150. Схема к задаче приведены на рис. 3, численные данные. в табл. 3.  =5 рад/с; r=24 см; l=36 см; α=300; =150. Решение Ускорение ползуна в данный момент времени можно найти с помощью векторной формулы распределения ускорений точек плоской фигуры, спроектировав ее на два взаимно перпендикулярные направления. В качестве полюса удобно принять точку А. 1. Изобразим положение механизма в соответствии с заданными углами (рис. 3.1). 2. Скорость точки А, как вращательную вокруг неподвижной точки О, определим по формуле  см/с. Для определения скорости точки В определим положение мгновенного центра скоростей Р (рис. 3.1), для чего покажем направления скоростей точек А и В, а затем из точек А и В восстановим перпендикуляры к их скоростям VA и VB. Точка пересечения перпендикуляров будет являться мгновенным центром скоростей Р. Рассматривая плоское движение шатуна в данный момент времени как вращательное относительно мгновенного центра скоростей Р, определим угловую скоростей шатуна см/с. Для определения скорости точки В определим положение мгновенного центра скоростей Р (рис. 3.1), для чего покажем направления скоростей точек А и В, а затем из точек А и В восстановим перпендикуляры к их скоростям VA и VB. Точка пересечения перпендикуляров будет являться мгновенным центром скоростей Р. Рассматривая плоское движение шатуна в данный момент времени как вращательное относительно мгновенного центра скоростей Р, определим угловую скоростей шатуна 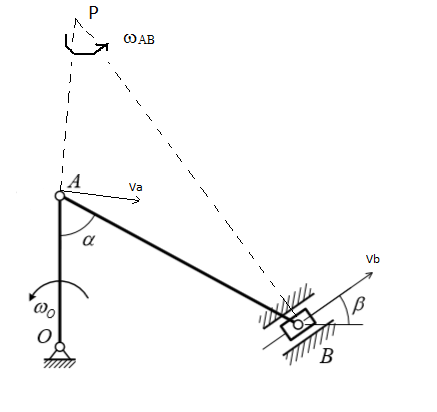 Рис 3.1. Схема к задаче Рассматривая плоское движение шатуна в данный момент времени как вращательное относительно мгновенного центра скоростей Р, определим угловую скоростей шатуна AB. 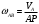 Расстояние AP определим из треугольника ABP: APB = ABP =150, следовательно, AP=AB=36 см.  рад/с рад/сСкорость точки В определим как вращательную относительно мгновенного центра скоростей Р: 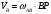 BP найдём по теореме синусов: 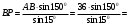 18 18  см/с см/сЗадача 3. Плоскопараллельное движение твердого тела. Кривошип ОА=r вращается вокруг оси О с постоянной угловой скоростью и приводит в движение шатун АВ=l и ползун В. Для заданного положения механизма найти скорость и ускорение ползуна В. Примечание. Если данные таковы, что шатун окажется перпендикулярным направляющей ползуна (схемы I, VI), то вместо заданного угла следует принять =15о. Схемы к задаче приведены на рис. 3, численные данные. в табл. 3.  =5 рад/с; r =24 см; l=36 см; α=30о; =15о. Решение | ||||||||||||||||||||||||||||||||||||||||
