погрешности. Определение погрешностей. Учебнометодическое пособие для студентов медицинского факультета СанктПетербург 2006

• Название: Учебнометодическое пособие для студентов медицинского факультета СанктПетербург 2006
• Анкор: погрешности
• Дата: 10.03.2022
• Размер: 411.5 Kb.
• Имя файла: Определение погрешностей.doc
• Тип: Учебно-методическое пособие; #390243

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕНННЫЙ УНИВЕРСИТЕТ
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
Б.Д. КАТУНИН

ОБРАБОТКА РЕЗУЛЬТАТОВ ФИЗИЧЕСКИХ ИЗМЕРЕНИЙ
Учебно-методическое пособие для студентов медицинского

факультета


Санкт-Петербург

2006

I. ВВЕДЕНИЕ

В ходе выполнения любой лабораторной работы приходится проводить физические измерения. Физические измерения представляют собой процесс, в котором устанавливается количественное соотношение между измеряемой величиной и её единицей измерения. Единица измерения должна представлять собой физическую величину того же рода, что и измеряемая величина. Так, за единицу длины принимается некоторая длина, за единицу времени - некоторый промежуток времени и т.д. и т.п.

В процессе измерений всегда присутствуют неточности, в силу чего истинное значение измеряемой физической величины никогда не может быть установлено.

Экспериментальные ошибки неизбежны вследствие целого ряда причин. Это и ограниченная точность измерительных приборов, и несовершенство теоретических модельных представлений, и невозможность полного устранения влияния на конечный результат измерений различных, сопутствующих измерениям, второстепенных явлений и еще многое другое. Поэтому в результате измерений всегда получаются не точные, а лишь приближенные значения измеряемых величин. Количественной мерой экспериментальных неточностей является погрешность измерения.

Основываясь на теории погрешностей, оказывается возможным установить величину погрешности измерения, то есть определить числовой интервал, в котором находится истинное значение измеряемой величины.

Основная задача физических измерений состоит в том, чтобы дать оценку истинного значения измеряемой величины и определить погрешность измерения.

Результаты измерений принято записывать в следующей форме:

x = x  x, (1)

где x - измеряемая физическая величина, x - оценка её истинного значения, а x - абсолютная погрешность, которая указывает величину возможного отклонения результата измерения x от истинного значения измеряемой величины x.

Запись результата измерений в форме (1) означает, что истинное значение измеряемой величины x находится в интервале значений от ( ) до ( ) и ничего более определенного об этой величине в ходе проведенного эксперимента узнать невозможно.

О точности измерения удобно судить по относительной погрешности x, которая выражается отношением абсолютной погрешности измерения к полученной оценке истинного значения измеряемой величины:

x = (%). (2)

x - безразмерная величина, обычно выражаемая в процентах.

Равенство (1) имеет вероятностный характер. Невозможно с полной уверенностью утверждать, что истинное значение лежит в указанных пределах, но имеется лишь некоторая вероятность (её называют доверительной вероятностью) этого.

Строгое определение x с указанием доверительной вероятности является сложной математической задачей, выходящей за рамки лабораторного физического практикума для студентов медицинского факультета СПбГУ, поэтому в настоящем пособии описывается упрощенная методика определения x, x и x, которая будет использоваться при обработке результатов измерений в ходе выполнения лабораторных работ.
II. ВИДЫ ИЗМЕРЕНИЙ.

В зависимости от способа получения результата принято различать прямые и косвенные измерения.

Измерения называются прямыми в тех случаях, когда есть прибор, позволяющий непосредственно измерить требуемую физическую величину. Например, к прямым измерениям относятся: измерения длины линейкой, времени - секундомером, массы - весами, температуры - термометром, силы тока – амперметром и т.п. .

Косвенными называют измерения, при которых искомую величину не измеряют непосредственно прибором, а вычисляют, пользуясь известной зависимостью искомой величины от других величин, которые возможно определить прямыми измерениями. Например, площадь поперечного сечения проволоки находят, измеряя её диаметр, плотность твердого тела правильной геометрической формы - находя массу и геометрические размеры, электрическое сопротивление проводника - измеряя силу тока в проводнике и напряжение на нем и т.п.
III. ТИПЫ ПОГРЕШНОСТЕЙ

При оценке точности результатов измерений различают и учитывают следующие основные типы погрешностей: систематические, случайные и промахи.

1. Систематические погрешности ( ) сохраняют свое значение и знак от опыта к опыту и не зависят от числа измерений.

Систематические погрешности могут быть обусловлены разными причинами, однако с большой надежностью их можно охарактеризовать приборной погрешностью - . Таким образом, при обработке экспериментальных данных будем считать, что . Действительно, если какой-либо прибор дает, например, завышенное значение, то он будет это делать при каждом измерении, причем одинаковым образом.

2. Случайные погрешности - x . Значения и знаки случайных погрешностей изменяются от опыта к опыту. Предсказать эти изменения невозможно. Обнаруживаются случайные погрешности при многократном измерении одной и той же величины одним и тем же прибором, одним и тем же методом. Случайные погрешности могут быть вызваны многими причинами, действующими в каждом отдельном измерении различным образом. Такими причинами могут быть: изменяющаяся температура, сотрясение фундамента здания, неоднородность объекта исследования, перепады напряжения в сети и т.д. и т.п. Суммарное действие многих случайных причин и вызывает заметные расхождения отдельных результатов измерений.

3. Промахи - это грубые ошибки, которые в большинстве случаев появляются в результате неправильных действий при проведении опыта и, таким образом, обусловливаются в основном низким уровнем квалификации экспериментатора, свидетельствуя, в частности, о плохой предварительной подготовке студента. Промахи следует выявлять и не учитывать при обработке результатов измерений. Например, если в результате нескольких измерений одной и той же величины все значения оказываются близкими, а одно отличается в несколько раз, то это промах.
IV. ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТИ ПРЯМЫХ ИЗМЕРЕНИЙ

Единичное измерение содержит случайную погрешность, а может содержать и промах. Для того, чтобы сделать результат достоверным необходимо произвести одно и тоже измерение несколько раз (считается достаточным сделать от трех до пяти измерений). Если после нескольких измерений воспроизводится один и тот же результат, то это свидетельствует либо о том, что приборная погрешность значительно больше случайной погрешности, либо о том, что случайная погрешность отсутствует. В этом случае измерения следует прекратить, считая, что x = x .

1. Как определить приборную погрешность x ?

Величина приборной погрешности может быть найдена одним из следующих способов:

1. 
   Приборная погрешность может быть указана или на самом приборе, или в его паспорте (в описании лабораторной работы).
   

2. 
   Приборная погрешность электроизмерительных приборов определяется по классу точности прибора. Класс точности указывается в нижней части шкалы прибора, как правило, в виде числа, обведенного в кружочек.
   

Например: 2.0 или 0.5 . Класс точности прибора равен
приборной погрешности, выраженной в процентах от максимального значения, измеряемого на данной шкале. Обозначим класс точности прибора буквой N. Тогда:
% . (3)

Таким образом, зная класс точности прибора N можно рассчитать приборную погрешность x по формуле:

. (4)

Пример. Пусть необходимо измерить силу тока амперметром класса




точности 0,05 и с диапазоном измерения (0 - 10) А. Абсолютную погрешность определим по формуле (4):

А.

Так как относительная погрешность зависит от значения измеряемой величины, то она оказывается тем меньше, чем ближе значение измеряемой величины к предельному значению шкалы. Так, в рассматриваемом примере, если измеренное значение тока оказалось бы равным 10А, то  %, а если 1А, то I = 0,5 %.

Следовательно, при работе с многопредельными приборами, в целях получения наименьшей погрешности измерения, следует выбирать такой предел измерения, при котором стрелка прибора имела бы максимальное отклонение.

3. В остальных случаях, когда отсутствует паспорт прибора и не указан класс точности, приборную погрешность следует считать равной половине наименьшего деления шкалы прибора (половине цены деления шкалы).

Пример. При измерении длины обычной линейкой, у которой наименьшее деление шкалы равно 1 мм, следует считать приборную погрешность равной 0,5 мм.
2. Как определить случайную погрешность x ?

Если после проведения нескольких измерений одной и той же физической величины обнаруживается, что она принимает различные значения после каждого измерения, то это свидетельствует о наличии случайной погрешности .

Допустим, что проделано n измерений физической величины x, и получены n её различных значений .

Оценку истинного значения измеряемой величины x принято находить как среднее арифметическое значение результатов измерений:

. (5)

Для того, чтобы вычислить абсолютную погрешность x 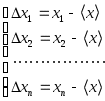следует найти разности между каждым из результатов отдельных измерений и среднеарифметическим значением:

(6)

Величины являются случайными отклонениями наблюдаемой величины от среднеарифметического значения и могут оказаться как положительными (если x x), так и отрицательными (если x  x ).

За величину погрешности принимается средняя абсолютная ошибка измерения, равная среднему арифметическому значению модулей случайных отклонений:

(7)

или

. (8)

3. Сложение погрешностей.

Полную погрешность измерения , учитывающую оба вида ошибок одновременно, принято определять следующим образом:

. (9)

Если можно сделать сколь угодно малой, увеличивая число измерений, то x является неизменной и для данного измерения определяет предельную минимальную погрешность (невозможно произвести измерение точнее, чем это позволяет сделать используемый измерительный прибор). Следовательно, число измерений имеет смысл увеличивать лишь до тех пор, пока средняя абсолютная ошибка измерений не станет равной погрешности прибора. Обычно выбирают n  10 .
V. АЛГОРИТМ ПРЯМЫХ ИЗМЕРЕНИЙ

Проведение эксперимента и обработка его результатов в случае прямых измерений осуществляются в следующей последовательности:

- следует ознакомиться с паспортными данными измерительного прибора и занести в протокол лабораторной работы название прибора и диапазон (шкалу), на котором производится измерение;

- определить и занести в протокол лабораторной работы приборную погрешность ;

- повторить от трех до пяти раз измерения величины x и установить наличие или отсутствие случайной ошибки:

а/ если все результаты повторных измерений одинаковы - случайной ошибки нет;

б/ разброс результатов свидетельствует о наличии в измерениях

случайной ошибки.

- в случае отсутствия случайной ошибки погрешность измерения принимают равной приборной погрешности, измерение следует считать законченным и в протокол заносится результат измерения в виде: .

- в случае обнаружения случайной ошибки необходимо продолжить измерения, доведя число повторных измерений величины x до десяти, а затем следует:

- найти оценку истинного значения:

.

- найти модули случайных отклонений:



- вычислить величину случайной погрешности :

.

- вычислить полную погрешность:



- записать окончательный результат измерений в виде:

.

Определение измеряемой величины x закончено.


VI. ПРАВИЛА ОКРУГЛЕНИЯ ПОГРЕШНОСТЕЙ И

ЗАПИСИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ
Абсолютная погрешность в предлагаемом способе оценки округляется до первой значащей цифры. Причем, при округлении последнюю из остающихся цифр следует увеличивать на единицу, если первая из отбрасываемых цифр больше либо равна 5. Если же первая из отбрасываемых цифр меньше 5, то последняя цифра остается неизменной.

Примеры:

x = 0,2874  0,3; x = 0,4036  0,4;

x = 2,45  2 x = 384  400 .

В приближенных вычислениях под значащими цифрами подразумеваются все цифры числа, кроме нуля, а также и нуль, когда:

- нуль стоит между значащими цифрами,

- нуль стоит в конце числа при отсутствии единиц соответствующего разряда.

Оценка истинного значения измеряемой физической величины округляется до того десятичного разряда, в котором указывается погрешность.

Примеры:

x = 652,43  0,1  652,4  0,1; x = 0,8024  0,06  0,80  0,06.

При записи конечного результата следует использовать стандартный вид числа: , где  10, n - целое число со знаком (+) или (-).

Примеры:




Число Стандартный вид числа Значения



n



2880 2,88 3

123,3 1,233 2

0,00541 5,41 -3

0,0103 1,03 -2
В записи конечного результата общий порядок числа следует выносить

за скобки. Например, правильная запись результата измерения массы вещества должна выглядеть так:

кг.

В записи результата измерений обязательно указывается размерность измеряемой физической величины.
VII. ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ

При косвенных измерениях результат вычисляется по формуле, устанавливающей связь измеряемой величины с другими величинами, которые определяются прямыми измерениями.

Пусть величина y связана с величинами известной функциональной зависимостью:

, (10)

которую будем называть расчетной формулой.

Пусть в результате прямых измерений определены все величины 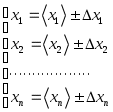. Это означает, что найдены оценки их истинных значений и абсолютные погрешности :

.

Оценку истинного значения величины «y» можно найти, воспользовавшись расчётной формулой (10), подставляя в последнюю оценки истинных значений величин :

. (11)

В основе вычисления погрешностей косвенных измерений лежит предположение, что абсолютные ошибки измерений всегда достаточно малы по сравнению с измеряемыми величинами. Это позволяет в математической теории ошибок абсолютные ошибки рассматривать как бесконечно малые приращения измеряемых величин.

Однако, чтобы подчеркнуть, что погрешности лишь условно рассматриваются как бесконечно малые, будем для их обозначения использовать не знак дифференциала «d», а по-прежнему, обозначать их .

Перед выводом общего правила, по которому определяется погрешность , рассмотрим простейший случай, когда косвенно измеряемая величина «y» является функцией лишь одной непосредственно измеряемой величины x: .

По определению производной функции:

, или

. (12)
Если обе части уравнения (12) разделить на y , то мы получим выражение, позволяющее рассчитать относительную погрешность y: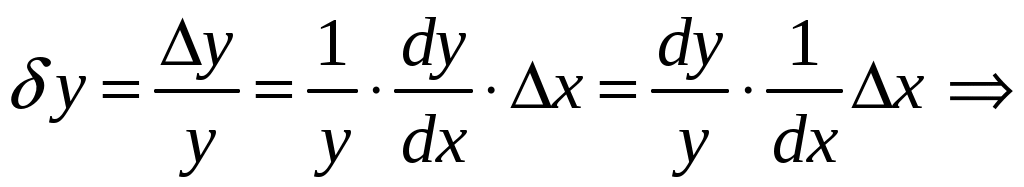



(13)

Рассмотрим теперь общий случай, когда косвенно измеряемая величина y зависит от n непосредственно измеряемых величин : . Частную погрешность , обусловленную измерением i - ой переменной можно найти по формуле:

. (14)

Здесь - частная производная функции «y» по аргументу . Она вычисляется так же, как и обычная производная, если считать остальные аргументы зафиксированными и рассматривать их как константы. Полную погрешность косвенного измерения можно найти, складывая частные погрешности. Однако, так как частные погрешности могут оказаться разного знака, а задачей является нахождение предельной погрешности, то складывать следует модули частных погрешностей - :

. (15)

Получим выражение для вычисления относительной погрешности:

 .

Таким образом, окончательная расчетная формула для вычисления относительной погрешности при косвенных измерениях выглядит так:

 , (16)

Используя (15) можно получить формулу для расчета предельной абсолютной погрешности . Мы видим, что для этого следует найти частные производные функции по всем её аргументам, умножить их на соответствующие абсолютные ошибки аргументов и модули полученных выражений сложить.

Однако, при выполнении лабораторных работ, как правило, будут встречаться функции, удобные для логарифмирования. В этом случае проще сперва определить относительную погрешность измеряемой величины y по формуле, выведенной с использованием соотношения (16), а уже затем, рассчитав оценку истинного значения y по формуле, получить абсолютную погрешность y:

y = yy . (17)

VIII. АЛГОРИТМ КОСВЕННЫХ ИЗМЕРЕНИЙ

В случае косвенных измерений следует:

1. 
   Занести в протокол лабораторной работы расчетную формулу с указанием названий всех аргументов .
   
2. 
   Вывести расчетную формулу для вычисления относительной погрешности dy. Для этого:
   

- найти натуральный логарифм выражения ,

- вычислить частные производные ,

- умножив частные производные на соответствующие им , получить окончательную формулу в соответствии с (16).

3. 
   Занести расчетную формулу для вычисления относительной погрешности в протокол лабораторной работы.
   

4. Произвести прямые измерения всех аргументов , то есть найти оценки их истинных значений   и абсолютных погрешностей  .

5. Занести результаты прямых измерений в протокол лабораторной работы.

6. Вычислить оценку истинного значения измеряемой величины .

7. 
   Произвести вычисление погрешности y, а затем и y.
   
8. 
   Записать в протокол измерений окончательный результат.
   

Определение измеряемой величины y закончено.

.

IX. ПРИМЕР ОБРАБОТКИ РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ

Пусть необходимо определить объём образца цилиндрической формы. Известно, что объём цилиндра можно рассчитать по формуле:

,

где D - диаметр и h - высота – величины, определяемые в процессе прямых измерений. Сам объём V измеряется косвенно. Выведем формулу для вычисления погрешности определения объёма. Сначала получим формулу для вычисления относительной погрешности V. Для этого прологарифмируем расчетную формулу, а затем продифференцируем её по всем аргументам.

После логарифмирования будем иметь:

.

Учитывая, что

и ,

после дифференцирования и умножения соответственно на D и Dh получим:

 .

Проведем прямые измерения D и h . Пусть измерение высоты производится при помощи обычной линейки с миллиметровыми наименьшими делениями. Приборную погрешность оцениваем в этом случае в половину цены деления: мм.

Пусть измерение высоты, проведенное несколько раз, дало 55,2 мм, причем разброс не был обнаружен. Отсутствие разброса результатов измерений свидетельствует о том, что случайной ошибки нет. Записываем результат измерения высоты в протокол лабораторной работы:

мм.

Измерение диаметра осуществляем при помощи микрометра с приборной погрешностью, указанной на самом приборе: мм.

Измерения диаметра, проведенные в различных местах под различными направлениями, дали отличные друг от друга результаты. Разброс результатов измерений свидетельствует о наличии случайной ошибки, возникновение которой вероятнее всего связано с отличием формы образца от идеальной. Результаты измерений и их обработку заносим в таблицу экспериментальных данных:



№№ D (мм) (мм)




1 22,58 0,01

2 22,57 0

3 22,60 0,03

4 22,54 0,03

5 22,55 0,02

6 22,58 0,01




СРЕДНЕЕ 22,5732 0,02



Так как в рассматриваемом случае оказалось, что , то полную погрешность диаметра следует рассчитать по формуле (9):

мм.

Округляем погрешность до первой значащей цифры и записываем окончательный результат измерения диаметра в протокол лабораторной работы: D = (22,57  0,03) мм.

Вычисляем оценку истинного значения объёма образца, подставляя в расчетную формулу оценки истинных значений высоты и диаметра:

мм .

Вычисляем относительную погрешность V по выведенной нами формуле:



Определяем абсолютную погрешность V по формуле (17) :

мм ,
или после округления: V = 300 мм

Округляем оценку истинного значения объёма образца до того разряда, в котором определена погрешность, и записываем окончательный результат измерений объёма в протокол лабораторной работы, переведя его предварительно в систему СИ:

м .

X. ГРАФИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ.

Пусть известно, что зависимость между физическими величинами x и y имеет вид



или

,

и требуется определить численные значения параметров или и по результатам измерений величин x и y.

В результате измерений получаем N пар экспериментальных значений x и y: . Для функции можно было бы, используя результаты каждого измерения, рассчитать N значений параметра и затем найти оценку истинного значения , рассчитав среднюю арифметическую величину всех . Однако существенно проще, построить график зависимости , проведя прямую через все экспериментальные точки и тем самым сразу усреднив результаты всех измерений, и определить , найдя угловой коэффициент прямой. В случае зависимости параметры и также могут быть легко определены после построения графика линейной функции.

Но, как это сделать? Как провести прямую линию, чтобы она прошла как можно ближе ко всем экспериментальным точкам. Можно это сделать на глазок, руководствуясь тем, что примерно одинаковое число экспериментальных точек должно оказаться по разные стороны проводимой линии. Однако существует аналитическое решение задачи построения графиков по экспериментальным точкам. Оно дается в методе наименьших квадратов.

XI. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.

Будем считать, что погрешность в определении численных значений параметров обусловлена только разбросом экспериментальных точек относительно теоретической прямой. Это значит, что абсолютные погрешности и настолько малы, что мы не будем принимать их во внимание.

1. Рассмотрим случай зависимости .

Экспериментально определенной величине соответствует точка с ординатой , лежащая на прямой и точка с ординатой , которая определена экспериментально. Следовательно, погрешность в определении величины y в данной i- й точке составляет:



Для исключения знаков 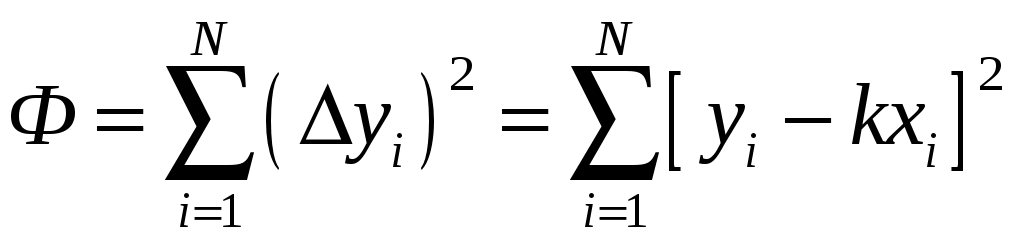удобно пользоваться квадратами этих погрешностей. Введем величину Ф, равную сумме квадратов :

.

Для того, чтобы провести прямую как можно ближе ко всем экспериментальным точкам, мы должны найти такое значение параметра , которое сведёт к минимуму сумму квадратов погрешностей, или, что тоже самое, найти минимум функции .

Таким образом, задача сводится к решению уравнения: .

Тогда, ,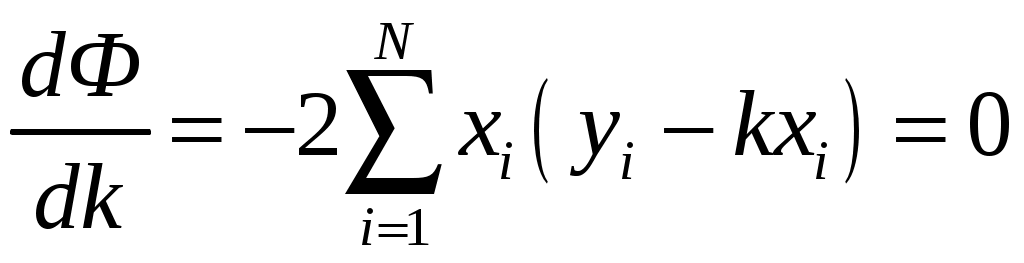

откуда .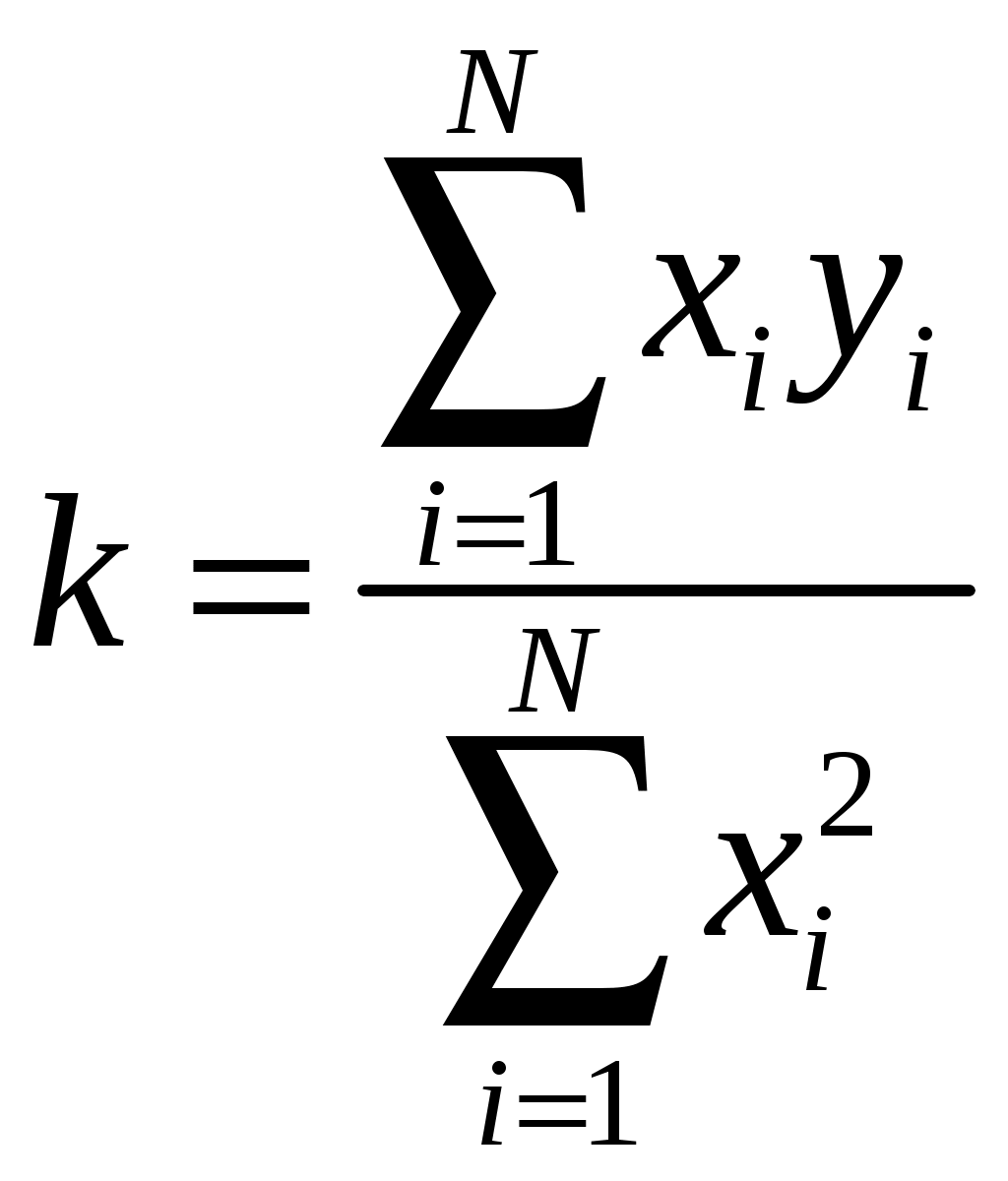

Можно показать, что в рассматриваемом случае абсолютная погрешность 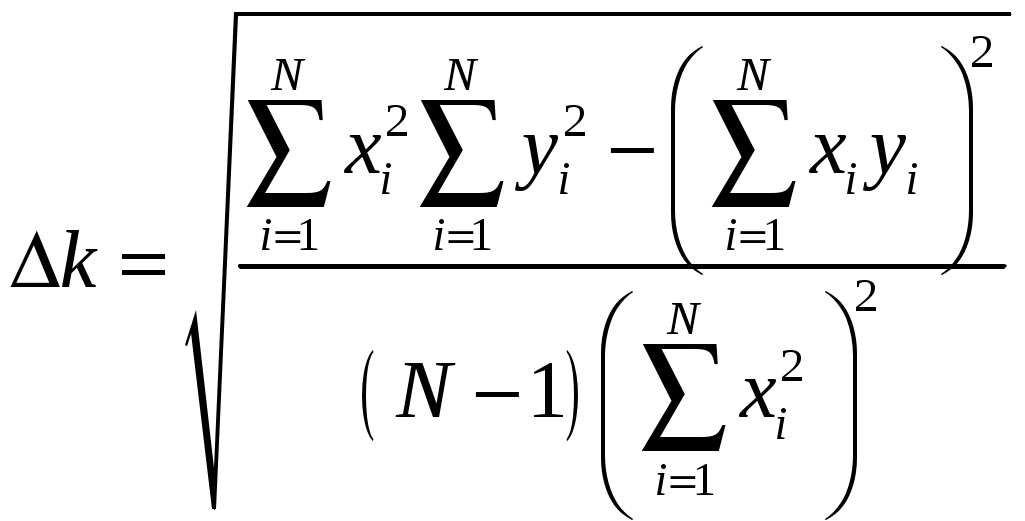определяется по формуле:

.

2. Случай зависимости 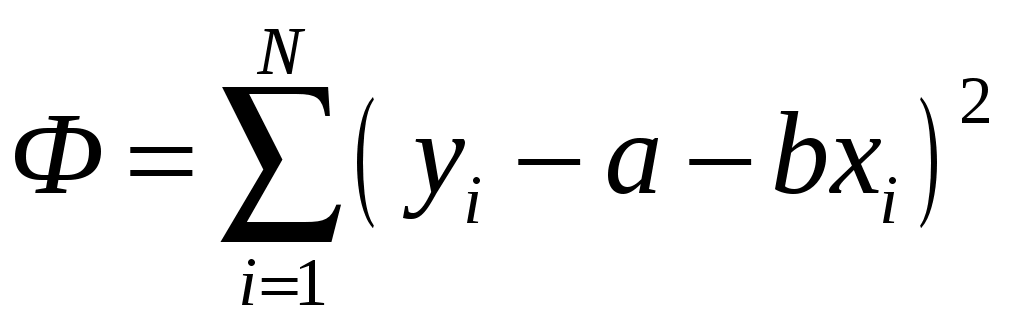. Снова составим сумму квадратов погрешностей:

и найдем значения параметров 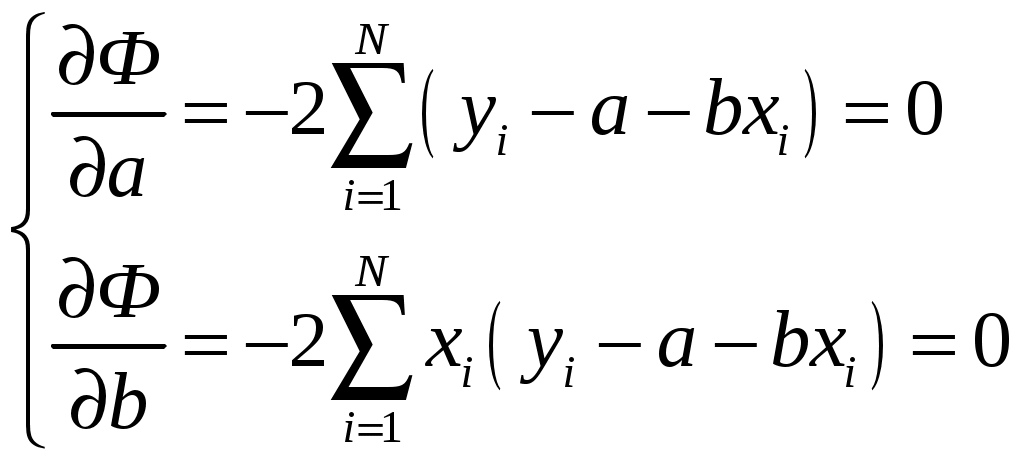и , при которых она минимальна. Для чего решим систему уравнений:

.

Совместное решение уравнений, входящих в систему дает: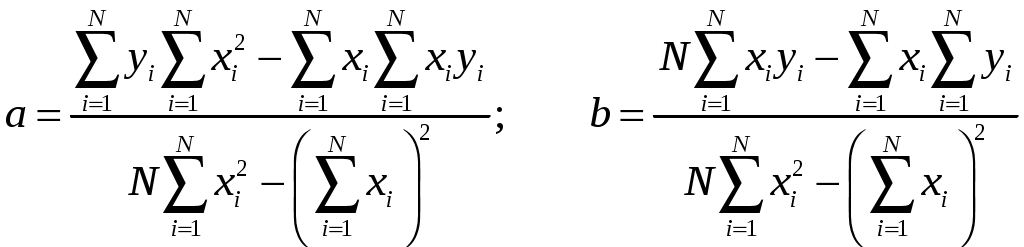

.

Полученные формулы принимают более простой вид, если ввести средние величины 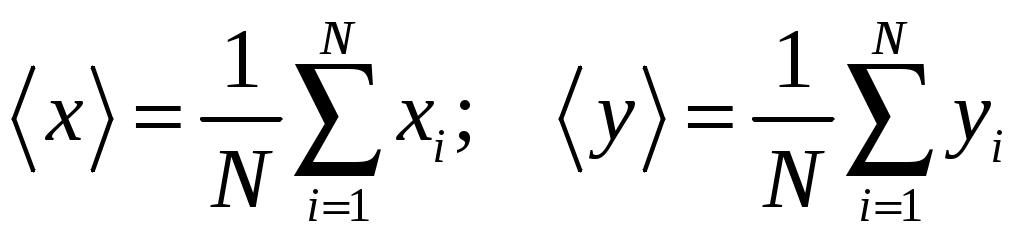и : .

Подстановка дает: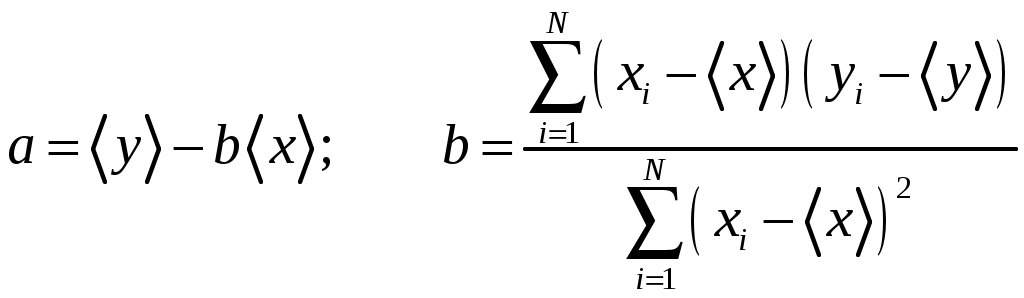

.

В заключение приведем без вывода формулы для определения абсолютных ошибок 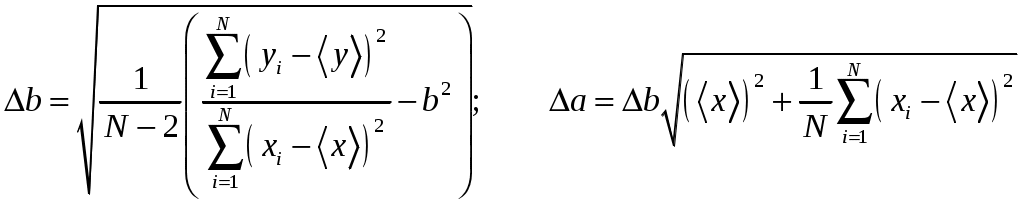и :

.