Тех.мех. Задача С1 Жесткая рама (рис. 0 9, табл. С1) закреплена в точке а шарнирно, а в точке
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
Ускорение 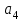 . . Т.к. рейка 4 совершает поступательное движение, то 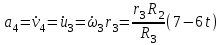 . . Тогда 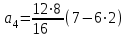 = –30 (см/с2). = –30 (см/с2).Ответ:
Задача К4 Прямоугольная пластина (рис. К4.0—К4.4) или круглая пластина радиуса R=60 см (рис. К4.5—К4.9) вращается вокруг неподвижной оси по закону φ=f1(t), заданному в табл. К4. Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. На рис. 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения ОО1лежит в плоскости пластины (пластина вращается в пространстве).По пластине вдоль прямой BD(рис. 0—4) или по окружности радиуса R(рис. 5—9) движется точка М; закон ее относительного движения, т. е. зависимость s=AM=f2(t) (s выражено в сантиметрах, t— в секундах), задан в таблице отдельно для рис. 0—4 и для рис. 5—9; там же даны размеры b и l. На рисунках точка М пока-зана в положении, при котором s=AM>0 (при s<0 точка М находится по другую сторону от точки А). Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1=1с. 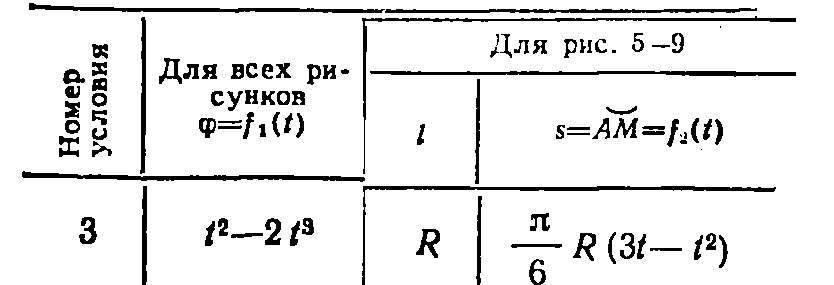 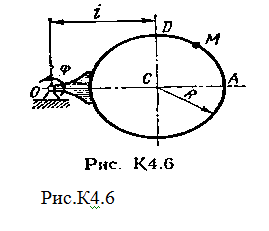 Дано: Точка М движется относительно пластины. Уравнение относительного движения т. М: 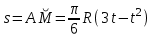 (см). Уравнение движения тела (см). Уравнение движения тела 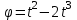 (рад). t=1 с; (рад). t=1 с; 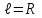 , , 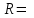 60 см. 60 см.Найти: Для заданного момента времени определить абсолютную скорость и абсолютное ускорение т.М. 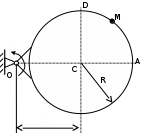 Решение РешениеРассматриваем движение т.М как сложное, считая ее движение по окружности относительным, а вращение пластины – переносным. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам: 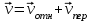 , ,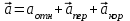 или в развернутом виде или в развернутом виде 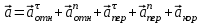 . .Положение т.М: При t=1с 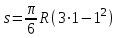 = =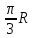 (см) – т.М находится в области положительных значений выше т.А. (см) – т.М находится в области положительных значений выше т.А.Тогда АСМ= 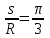 = 60о, а DСМ=30о. = 60о, а DСМ=30о. Расстояние от оси вращения О до т.М :  =104 (см). =104 (см). Относительное движение. Относительная скорость 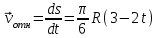 . . При 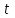 = 1 с = 1 с 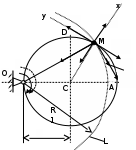 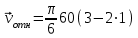 = 31,4 (см/с) – вектор направлен в сторону положительных значений = 31,4 (см/с) – вектор направлен в сторону положительных значений 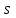 . .Модуль относительной скорости 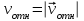 =31,4 см/с. =31,4 см/с.Модуль относительного касательного ускорения 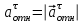 , где , где 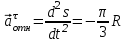 . . При 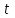 =1с =1с 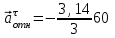 = –62,8 (см/с2). = –62,8 (см/с2). Значит 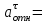 62,8 (см/с2). 62,8 (см/с2).Вектор 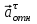 направлен в сторону отрицательных значений направлен в сторону отрицательных значений 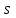 . Знаки . Знаки 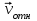 и и 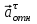 разные, следовательно, относительное движение т.М замедленное. разные, следовательно, относительное движение т.М замедленное.Относительное нормальное ускорение 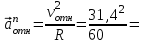 16,4 (см/с2). 16,4 (см/с2).Переносное движение. Модуль переносной скорости 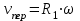 , , где R1 – радиус окружности L, описываемой той точкой тела, с которой совпадает в данный момент т.М 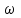 – модуль угловой скорости тела: – модуль угловой скорости тела: 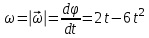 . .При 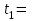 1 с 1 с 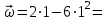 –4 1/с; –4 1/с; 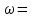 4 рад/с. 4 рад/с.Модуль переносной скорости: 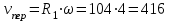 (см/с). Вектор (см/с). Вектор 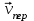 направлен по касательной к окружности L в сторону вращения тела. направлен по касательной к окружности L в сторону вращения тела.Модуль переносного вращательного ускорения 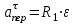 , где , где 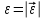 - модуль углового ускорения тела Д: - модуль углового ускорения тела Д: 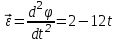 При 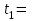 1 с 1 с 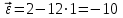 (1/с2); то есть переносное вращательное движение –ускоренное, так как знаки (1/с2); то есть переносное вращательное движение –ускоренное, так как знаки 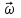 и и 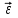 одинаковы. одинаковы. Значит 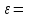 10 1/с2 и 10 1/с2 и 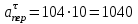 (см/с2). (см/с2).Вектор 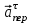 направлен в по направлен в по 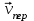 . .Модуль переносного центростремительного ускорения 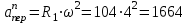 (см/с2). (см/с2). Вектор 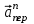 направлен от т .М к оси вращения. направлен от т .М к оси вращения.Кориолисово ускорение 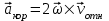 . .Модуль кориолисова ускорения 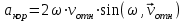 , где , где 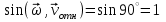 . . Так как 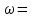 4 рад/с, а 4 рад/с, а 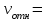 31,4см/с, то 31,4см/с, то 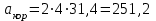 (см/с2). (см/с2).Вектор 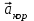 направлен в соответствии с правилом векторного произведения. направлен в соответствии с правилом векторного произведения.Абсолютная скорость. Абсолютную скорость т.М найдем как геометрическую сумму относительной и переносной скоростей. Векторы 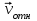 и и 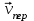 расположены под углом 150о (см. рисунок) друг к другу. расположены под углом 150о (см. рисунок) друг к другу.Модуль абсолютной скорости 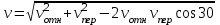 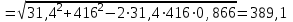 (см/с) (см/с)Абсолютное ускорение. Все векторы лежат в плоскости чертежа. Модуль абсолютного ускорения находим методом проекций: 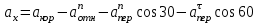 = =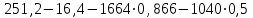 = –1726,2 (см/с2) = –1726,2 (см/с2)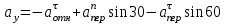 = =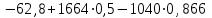 = –131,4(см/с2) = –131,4(см/с2)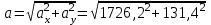 =1731 (см/с2) =1731 (см/с2)ДИНАМИКА Задача Д1 Груз Dмассой т, получив в точке А начальную скорость Vо, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0—Д1.9, табл. Д1). На участке АВ на груз кроме силы тяжести действуют постоянная сила Q(ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости V груза (направлена против движения); трением груза о трубу на участке АВ пренебречь. В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу f=0,2) и переменная сила 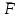 , проекция которой Fxна ось х задана в таблице. , проекция которой Fxна ось х задана в таблице.Считая груз материальной точкой и зная расстояние АВ = lили время t1движения груза от точки A до точки B,найти закон движения груза на участке ВС, т. е. x=f(t), где x=BD. 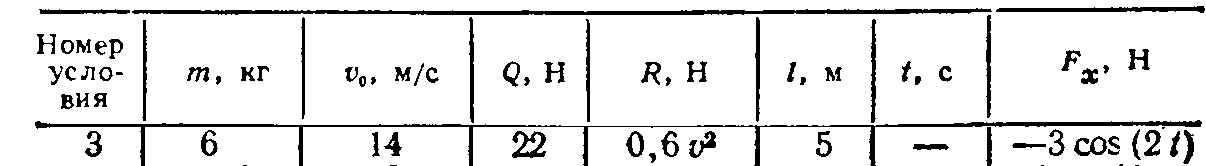  Дано: 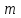 =6 кг, =6 кг, 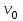 =14 м/с, Q=22 Н, R= =14 м/с, Q=22 Н, R=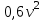 Н, Н, 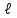 =5 м, =5 м,  Н, Н, 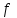 =0,2. =0,2.Найти: 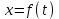 - закон движения груза на участке ВС - закон движения груза на участке ВСРешение 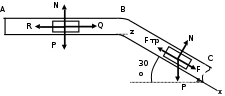 1) Рассмотрим движение груза на участке АВ, считая груз материальной точкой. На груз действуют сила тяжести 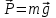 , реакция стенки , реакция стенки 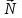 постоянная сила постоянная сила 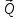 и сила сопротивления и сила сопротивления 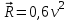 . . Проведем ось 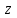 вдоль АВ. Составим дифференциальное уравнение движение в проекции на эту ось: вдоль АВ. Составим дифференциальное уравнение движение в проекции на эту ось: 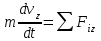 или или 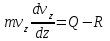 . . Перепишем это уравнение с учетом того, что 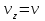 : : 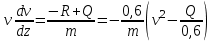 . Обозначим . Обозначим 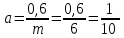 и и 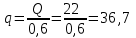 . Тогда . Тогда 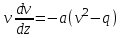 , разделяя переменные , разделяя переменные 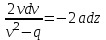 интегрируем: интегрируем: 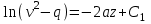 . . Постоянную С1 находим по начальным условиям: при 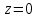 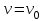 , что дает , что дает 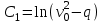 . Следовательно . Следовательно 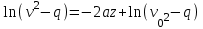 или или 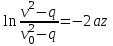 Отсюда получаем 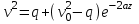 . .При перемещении груза в точку В 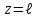 =5 м, =5 м, 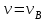 . . Тогда 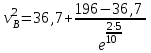 =95,3 и =95,3 и 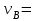 9,76 м/с. 9,76 м/с.2). При рассмотрении движения груза на участке ВС найденная скорость будет для движения на этом участке начальной скоростью. Составим дифференциальные уравнения движения груза в проекции на оси 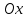 и и 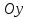 . .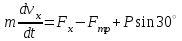 и и 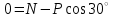 Тогда 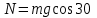 , , 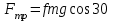 и и 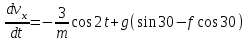 . . Обозначим 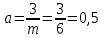 и и 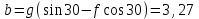 . Разделяя переменные и интегрируя, получим . Разделяя переменные и интегрируя, получим 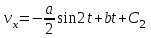 При начальных условиях 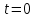 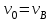 и и 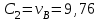 . То есть . То есть 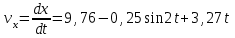 . .После интегрирования: 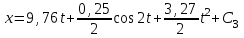 . . Т.к. при 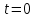 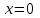 , то , то 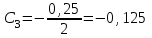 и окончательно искомый закон движения груза на участке ВС будет и окончательно искомый закон движения груза на участке ВС будет 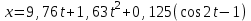 Задача Д4 Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3=0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4=0,2 м и катка (или подвижного блока) 5 (рис. Д4.0—Д4.9, табл. Д4); тело 5 считать сплошным однородным цилиндром, а массу блока 4—равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f=0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.Под действием силы F=f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках). Определить значение искомой величины в тот момент времени, когда перемещение s станет равным S1=0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: V1, V2,V3, Vc5— скорости грузов 1, 2 и центра масс тела 5 соответственно, ω3 и ω4 - угловые скорости тел 3 и 4.Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 1), катятся по плоскостям без скольжения.На всех рисунках не изображать груз 2, если m2=0; остальные тела должны изображаться и тогда, когда их масса равна нулю.  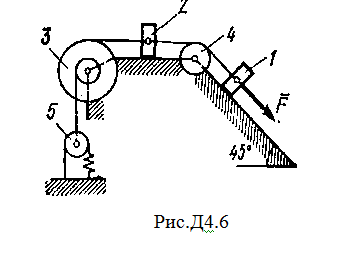  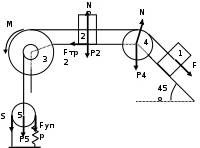 Дано: 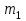 =0 кг, =0 кг, 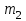 =6 кг, =6 кг, 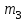 =0 кг, =0 кг, 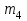 =5 кг (равномерно распределена по ободу), =5 кг (равномерно распределена по ободу), 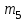 =4 кг (сплошной однородный шкив), с=300 Н/м, М=1,8 Нм, =4 кг (сплошной однородный шкив), с=300 Н/м, М=1,8 Нм, 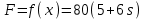 Н, Н, 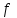 =0,1, =0,1, 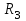 =0,3 м, =0,3 м, 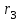 =0,1 м, =0,1 м, 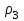 =0,2 м, =0,2 м, 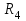 =0,2 м, =0,2 м, 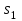 =0,2 м. =0,2 м.Найти: 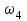 в тот момент времени, когда в тот момент времени, когда 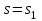 | |||||||||||||||
