теоретическая механика. Задача С1 Определить реакции опор. G 10 кН m 20 кНм q 5 кНм. 60
 Скачать 120.01 Kb. Скачать 120.01 Kb.
|
|
Вар-т 8 Задача С1 Определить реакции опор. G = 10 кН; M = 20 кНм; q = 5 кН/м. α = 60  . . 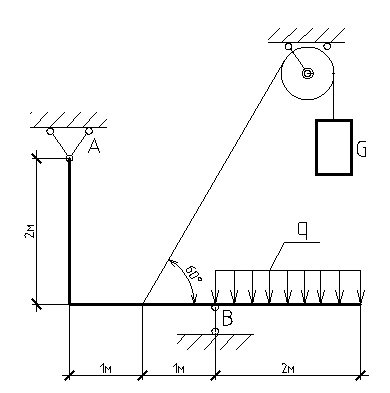 Убираем связи – опоры А и В и заменяем их действие реакциями. Из точки закрепления троса к балке прикладываем силу G. Система геометрически неизменяема, так как линии действия реакций не сходятся в одной точке. Распределённую нагрузку заменим на сосредоточенную Q = q·2 = 5·2 = 10 кН,(но это не обязательное требование!). 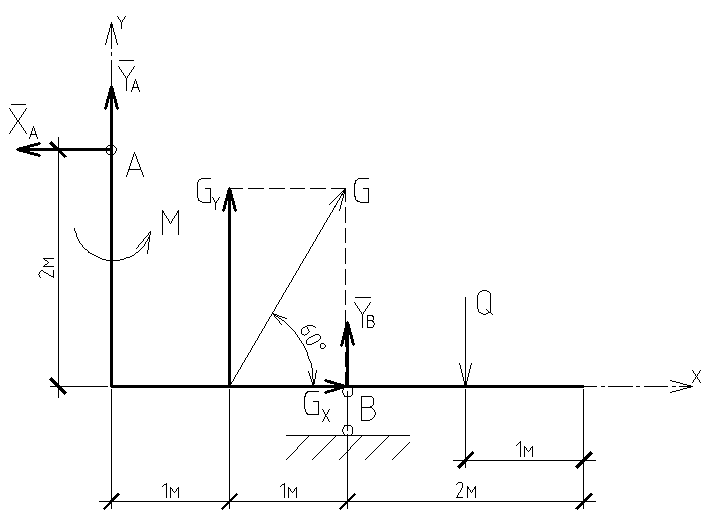 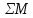 А = 0; GY = G·cos30 А = 0; GY = G·cos30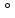 = 10·0,866 = 8,66 кН, = 10·0,866 = 8,66 кН,GX = G·sin30 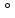 = 10·0,5 = 5 кН. = 10·0,5 = 5 кН.YB·2 + M + GY·1 + GX·2 - Q·3 = 0, YB = (- M - GY·1 - GX·2 + Q·3)/2 = (-20 - 8,66·1 - 5·2 + 10·3)/2 = - 4,33 кН, знак «минус» означает, что реакция направлена противоположно первоначальному направлению на рисунке. 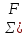 k)x = 0; k)x = 0;- XA + G·cos60 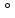 = 0, = 0,XA = G·cos60 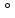 = 10·0,5 = 5 кН. = 10·0,5 = 5 кН.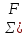 k)y = 0; k)y = 0;YA + GY - YB - Q = 0, YA = - GY - YB + Q = - 8,66 + 4,33 + 10 = 5,67 кН. Задание К-1. Точка С движется по плоскости хОу. Закон движения точки С задан двумя уравнениями: х = f1(t). y = f2(t), где х и у выражены в метрах, t – в секундах. х = 3cos( 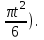 у = 3sin( 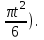 (1) (1)Определить уравнение траектории точки С, определить скорость, ускорение точки С, а также касательное и нормальное ускорения и радиус кривизны в точке С траектории для момента времени t1 = 1с и всё изобразить графически. Решение. Исключим из системы уравнений время t. cos2(  = = 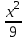 , sin2( , sin2( = = 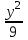 , ,cos2(  + sin2( + sin2( = 1, = 1,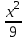 + + 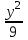 = 1 - уравнение окружности с радиусом R = 3м и с центром в начале прямоугольных координат. = 1 - уравнение окружности с радиусом R = 3м и с центром в начале прямоугольных координат.Далее определим положение точки С на траектории в момент времени t1 = 1c. Для этого в уравнения (1) подставим значение t = 0с. Получим хс = 2,598; ус = 1,5; т.е. С(2,598;1,5), обозначим т.С на траектории. 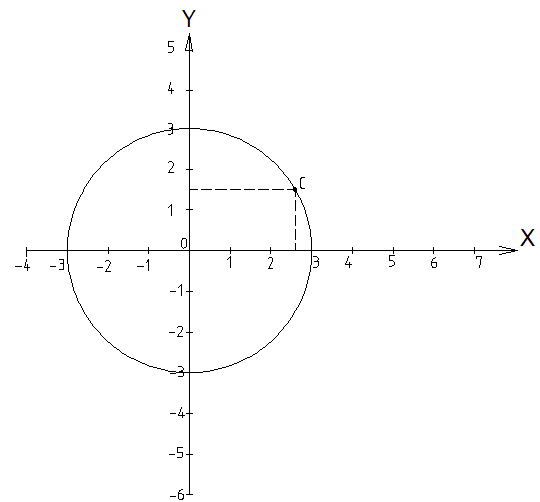 Далее определим две составляющие скорости т.С по осям Х и У: Vx = x´ = dx/dt = - πtsin(  . .Vy = y´ = dy/dt = πtcos(  . .При t = 1с Vx = - 3,14·1·0,5 = - 1,57 м/с; Vy = 3,14·1·0,866 = 2,7193 м/с; Модуль скорости Vс =  (Vx2 + Vy2) = (Vx2 + Vy2) =  (1,572 + 2,71932) = 3,14 м/с. (1,572 + 2,71932) = 3,14 м/с.Изобразим все три вектора на чертеже. 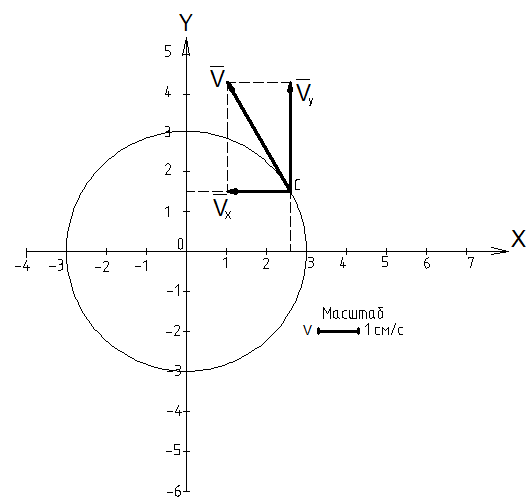 Из построения видно, что скорость Vс направлена по касательной к траектории в данной точке С. В точке С проведём взаимно перпендикулярные оси, получим касательную ось τ и нормальную ось n. Аналогично определим составляющие ускорения т. С: ахс = V´x = dVx/dt = - π2t2cos(  . .аус = V´у = dVу/dt = - π2t2sin(  . .При t = 1с, ахс = - 3,142·12·0,866 = - 8,5385 м/с2. аус = - 3,142·12·0,5 = - 4,9298 м/с2. ас =  ( а2хс + а2ус) = 9,8595 м/с2. ( а2хс + а2ус) = 9,8595 м/с2.Касательное ускорение определим по формуле аτ = (Vx·ax + Vy·ay)/V = [(-1,57)·(-8,5385) + 2,7193·(-4,9298)]/3,14 = 0м/с2. Точка С в момент t = 1с движется по траектории равномерно. Нормальное ускорение асn =  (a2c – a2τ) = (a2c – a2τ) =  (9,85952 – 0) = 9,8595 м/с2. (9,85952 – 0) = 9,8595 м/с2.Радиус кривизны ρ = V2/an; ρ = 3,142/9,8595 = 1,0 м  Задание 3 В момент выключения мотора катер массой т = 200 кг имел скорость V0 . Определить путь, который пройдет катер до того момента времени, когда скорость катера уменьшится в десять раз. Сила сопротивления движению пропорциональна квадрату скорости R = 8v2 . На катер действуют три силы: сила тяжести mg, архимедова сила Gи сила сопротивления R = 8v2 , где 8 – постоянный коэффициент (α) жидкостного сопротивления. Первые две силы вертикальны, а сила сопротивления горизонтальна и направлена в сторону, противоположную скорости катера. 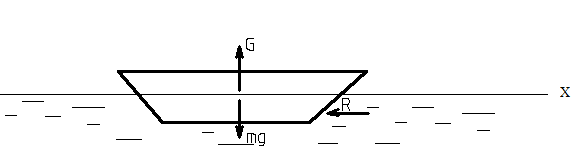 Основное уравнение динамики m 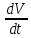 = mg + G + R. = mg + G + R.В проекции на ось х получим 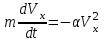 . .Перепишем это уравнение в виде 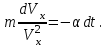 После интегрирования получим  (1) (1)Условимся считать время с момента остановки двигателей катера. Тогда при t = 0 Vx = V0и, следовательно, С = 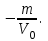 Выражение (1) теперь запишется в виде 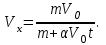 (2) (2)Так как Vx = 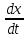 , то , то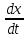 = = 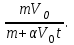 и, следовательно, х = 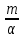 ln(m + αV0t) + C2. (3) ln(m + αV0t) + C2. (3)Постоянную C2найдём из условия: х = 0 при t = 0, т.е. 0 = 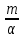 lnm + C2., и равенство (3) принимает вид lnm + C2., и равенство (3) принимает вид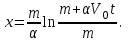 Подставив сюда соотношение  получаемое из формулы (2), окончательно имеем 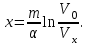 Полагая Vx = V0/10, найдём путь, который пройдёт катер за время, в течение которого его скорость уменьшится в 10 раз S = 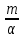 ln10 = ln10 =  ·1 = 25м. ·1 = 25м. |
