Задача состоит из Условия это то, что известно в задаче Вопроса это то, что надо узнать в задаче
 Скачать 108.5 Kb. Скачать 108.5 Kb.
|
|
Тема. Текстовая задача, ее составные части. Текстовая задача - это описание некоторой ситуации (процесса, явления) на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между ее компонентами или определить вид этого отношения. Задача состоит из: 1. Условия – это то, что известно в задаче;
4. Ответа - это число, полученное после выполнения действий. Различают: а) определенные задачи — в них заданных условий столько, сколько необходимо и достаточно для получения ответа; б) недоопределенные задачи — в них условий недостаточно для получения ответа. В начальной школе - это задачи с недостающими данными; в) переопределенные задачи - в них имеются лишние условия. В начальной школе - это задачи с избыточными данными. Задача с недостающими данными: «Из зала вынесли сначала 12 стульев, потом еще 5. Сколько стульев осталось в зале?» Задача с избыточными данными: «Возле дома росло 5 яблонь, 2 вишни и 3 березы. Сколько фруктовых деревьев росло возле дома?» Моделирование в процессе решения текстовых задачТекстовая задача - это словесная модель явления (ситуации, процесса) поэтому в ней описывается не все явление в целом, а лишь его количественные характеристики. Чтобы решить такую задачу, надо перевести ее на язык математических действий, т.е. построить ее математическую модель. Математическая модель - это описание, какого либо реального процесса на языке математических понятий, формул и отношений (выражение, запись действий, уравнение, система уравнений) Поэтому процесс решения задачи - это переход от словесной модели к математической. Этапы математического моделирования I этап - это перевод условий задачи на математический язык; при котором выделяются необходимые для решения данные и искомые и математическими способами описываются связи между ними; II этап - внутримодельное решение (т.е. нахождение значения выражения, выполнение действий, решение уравнения); III этап - интерпретация, т.е. перевод полученного решения на тот язык, на котором была сформулирована исходная задача. Наибольшую сложность в процессе решения текстовой задачи представляет перевод текста с естественного языка на математический, т.е. I этап математического моделирования. Чтобы облегчить этупроцедуру, строят вспомогательные модели - схемы, таблицы и др. Тогда процесс решения задачи можно рассматривать как переход от одной модели к другой: от словесной модели реальной ситуации, представленной в задаче, к вспомогательной (схемы, таблицы, рисунки и т.д.); от нее - к математической, на которой и происходит решение задачи. Виды моделей  Схематизированные модели Знаковые модели1. Вещественные модели: 1. Знаковые модели, а) предметы (пуговицы, выполненные на спички, полоски, счетный естественном языке: материал и т.д.); а) краткая запись, б) инсценировка сюжета б) таблица, задачи; 2. Знаковые модели в) мысленное выполненные на представление ситуации математическом языке описанной в задаче. (решающие модели): 2. Графические модели: а) выражение; а) рисунок; б) запись решения по действиям: б) условный рисунок; в) уравнение; в) чертеж; г) система уравнений. г) схема. Вспомогательными моделями, являются все схематизированные и знаковые модели, выполненные на естественном языке. Они обеспечивают переход от словесной модели задачи к ее математической модели. Рисунок, условный рисунок, чертеж, схема, краткая запись, таблица являются моделями задачи, если в них отражены:
Методы и способы решения текстовых задач. Различают следующие методы решения текстовых задач: 1. Арифметический метод. Ответ на вопрос задачи получаем, выполнив арифметические действия с числами. Одну и туже задачу можно решить различными арифметическими способами. Арифметические способы решения задачи считаются различными, если они отличаются хотя бы одним действием. Пример № 2. Задача «Сшили 4 платья, расходуя на каждое по 6 м ткани. Сколько кофт можно было сшить из этой ткани, если расходовать на одну кофту 3 м?» 1 способ
2 способ 1)6:3 = 2 (раза) - во столько раз больше идет ткани на платье, чем на кофту; 2) 4 * 2 = 8 (кофт) - столько кофт можно сшить 2. Алгебраический метод. Ответ на вопрос задачи получаем, составив и решив уравнение или систему уравнений. Алгебраические способы считаются различными, если при решении одной и той же задачи составляются различные уравнения или системы уравнений. Пример № 3. Задача «Свитер, шапку связали из 1 кг 200 г шерсти. На шарф потребовалось на 100 г шерсти больше, чем на шапку, и на 400 г меньше, чем на свитер, Сколько шести израсходовали на каждую вещь?». 1 способ Обозначим через х (г) массу шерсти, израсходованной на шапку Тогда на шарф будет израсходовано (х + 100) г, а на свитер ((х + 100) + 400) г. Так как на все три вещи израсходовано 1200 г, то можно составить уравнение. х+(х+100) + ((х+ 100) -+400)= 1200. Выполнив преобразования, получим, что х = 200. Таким образом, на шапку было израсходовано 200 г, на шарф - 300 г, так как 200 + I00 = 300, га свитер - 700 г, так как (200 + 100) + 400 = 700. 2 способ. Обозначим через х (г) массу шерсти, израсходованной на шарф. Тогда на шапку будет израсходовано (х - 100) г, а на свитер - (х +400) г. Поскольку на все три вещи израсходовано 1200. то можно составить уравнение: х + (х- 100) + (х + 400)=1200 Зх = 900 Выполнив преобразования, получим, что х = 300. Таким образом, если на шарф израсходовали 300 г, то на шапку 200 г (300 -100 = 200г а на свитер 700 г (300 + 400 = 700). 3 способ. Обозначим через х (г) массу шерсти, израсходованной на свитер. Тогда ша шарф будет израсходовано (х -400) г, а на шапку (х - 400 - 100) г. Поскольку на все три веще израсходовали 1200 г, то можно составить уравнение: х + (х - 400) + (х - 500)=1200. Выполняв преобразования, получим, что х = 700. Таким образом, если на свитер израсходовано 700 г, то на шарф пошло 300 г (700 - 400 = 300), а на шапку-200 г(700-400-100 = 200) 3.Графический метод. Ответ на вопрос задачи дается в процессе построения отрезков или измерения длин отрезков. Пример № 4. Задача « Из двух пунктов навстречу друг другу вышли два пешехода. Первый прошел Изобразим произвольным отрезком расстояние между пунктами. Опираясь на теорему Фалеса. разделим отрезок на 8 и на 10 равных частей. Опираясь только на чертеж, легко дать ответ на вопрос задачи: «Встреча не произошла». Такой способ решения можно назвать графическим. 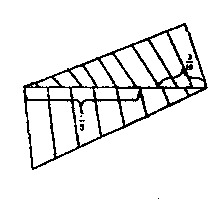 4. Практический метод. Ответ на вопрос задачи дается в результате выполнения действий с предметами. Пример №5. Задача. «В совхозе 40 автомашин - легковых и | грузовых, причем на каждую легковую машину приходится 4 грузовые. Сколько легковых и сколько грузовых машин в совхозе?». Изобразим каждую машину палочкой (40 машин - 40 палочек). Известно, что на каждую легковую машину приходится 4 грузовые. Поэтому отложим одну палочку — это легковая машина Под ней положим 4 палочки — это 4 грузовые машины. Будем поступать так до тех пор, пока все 40 палочек не окажутся разложенными. Чтобы ответить на вопрос задачи, достаточно сосчитать, сколько, палочек положено в верхнем ряду и сколько палочек положено в нижнем ряду. Этапы решения задач арифметическим способом. 1этап. Ознакомление с содержанием задачи. Назначение этапа:
Приемы, способствующие пониманию содержания задачи: 1. Задание специальных вопросов У –О чём(о ком )говорится в задаче? У. - Что известно в задаче? У. - Что неизвестно в задаче? У. - Что обозначают тс или иные слова в тексте задачи? У. - Что требуется найти в задаче? 2. Разбиение текста на смысловые части: У. - О ком говорится в задаче? У. - Что известно о первом пешеходе? У. - Что известно о втором пешеходе? У. - Какой главный вопрос задачи? 3 Переформулировка текста задачи Переформулировка текста задачи заключается в замене данного в задаче описания некоторой ситуации другим, сохраняющим все отношения, связи, количественные характеристики, но более явно их выражающим, т.е. преобразование текста задачи в форму, удобную для поиска решения. Главным средством переформулировка текста задачи является создание вспомогательной модели задачи. Запись переформулированного текста может быть оформлена в виде рисунка, условного рисунка, чертежа, схемы, краткой записи, таблицы. Цель этапа считается достигнутой, если ученик может повторить задачу по ее вспомогательной модели. Приведем пример работы над задачей в начальной школе. Задача: «На поезде, который шел со скоростью 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем проехал. Каков весь путь туриста?» I этап. Ознакомление с содержанием задачи 1) Вопросы по тексту У. - Читаем задачу про себя. У. - Кто прочитает задачу вслух? У. - О ком говорится в задаче? У.-Что делал турист? О. Ехал на поезде. У. - Что известно в задаче? О. - Скорость поезда У-Что ещё известно?. О- Сколько времени он ехал. О- Что ему осталось проехать в 4 раза больше, чем проехал, О. - Сколько км он уже проехал. - Сколько км ему осталось проехать. У. - Какой главный вопрос задачи? О. - Какой весь путь туриста? 2) Запишем задачу кратко (составим вспомогательную модель) У. - Какие слова помогут записать задачу кратко? О. - Проехал. Осталось. У. - Известно ли, сколько км. проехал турист? О.- Нет. У. - Как это обозначим? 0.-?км У. - Что обозначает 56 км/ч? О.- Скорость поезда. У. - Что обозначает 6 ч? О. - Сколько времени турист был в пути. У. - Как мы это запишем? О.-По 56 км/ч-6 ч. У. - Известно ли сколько км осталось туристу проехать? О.- Нет. У. - Как это обозначим? О. - ? км. У, - А что говорится о расстоянии, которое ему осталось проехать? О. - в 4 раза больше (запись на доске) У. - Что надо узнать в задаче? О. - Какой весь путь. У. - Как это обозначим? О.- }-?км 3) Кто повторит задачу по краткой записи? Вспомогательная модель задачи в виде краткой записи имеет вид: П 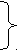 роехал -? км, по56км/ч- 6ч роехал -? км, по56км/ч- 6ч ? к м Осталось— ? км, в4раза б II этап .Поиск плана решения задачи Назначение этапа: - установить связь между данными и исходными объектами; - наметить последовательность действий. II. Поиска плана решения задачи арифметическим способом: Одним из приемов поиска плана решения задачи является разбор задачи. Разбор задачи может быть но тексту иди вспомогательной модели. В зависимости от цепочки рассуждений разбор задачи может быть:
Разбор задачи начинается с анализа задачи (разбиением задачи на части) и заканчивается составлением плана(синтезом). Приведем примеры разбора задачи: «На поезде, который шел со скоростью 56 км/ч Турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем проехал. Каков весь путь туриста?» Разбор задачи от вопроса к числовым данным. Схема разбора задачи от вопроса к числовым данным:  Надо знать 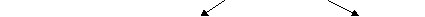 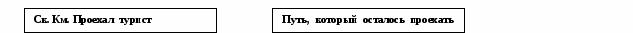 Надо знать Надо знать      Известно Неизвестно Надо знать   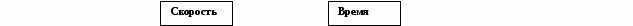 Разбор учителем задачи от вопроса к числовым данным: 1) Анализ задачи. У, - Что опрашивается в задаче? О. -Каков весь путь турист У. - Можем ли мы это узнать сразу? О.- Нет. У. - Почему? Чего мы ее знаем? О. - Сколько км уже проехал турист и сколько км ему осталось проехать. У. - А можем ли сразу узнать, сколько км туристу осталось проехать»? О. - Нет. У. - Почему, чего не знаем? О. - Сколько км он уже проехал. У. - А можем ли сразу узнать, сколько км он уже проехал? О.- Да. У. – Почему. Что знаем? О. - Скорость и время, 2) Составим план решения задачи. У. - Что узнаем вначале? О. - Сколько км уже проехал турист. У - Каким действием узнаем? О. - Умножением. У. - Что на что умножим? О. - Скорость на время У. - Что узнаем затем? О. - Расстояние, которое ему осталось проехать. У.- Каким действием? О. – Умножением. У. -Что на что умножим? О. - Пройденный путь на 4. У. - Что узнаем затем? О. - Каков весь путь туриста. У. - Каким действием? 0.- Сложением. У.- Что сложим? О. – Расстояние, которое турист проехал и расстояние, которое ему осталось проехать. У. - Кто запишет решение задачи по действиям с пояснением? - Кто запишет решение задачи выражением и ответ? Разбор задачи от числовых данных вопросу. Схема разбора задета от числовых данных к вопросу. 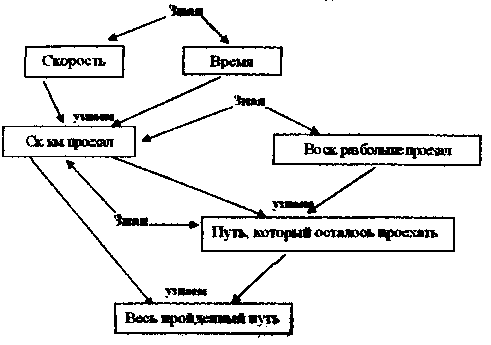 Разбор учителем задачи от числовых данных к вопросу. У. - Зная скорость поезда, и что турист на нем ехал 6 ч, что можно узнать? О. - Расстояние, которое проехал турист. У. - Каким действием узнаем расстояние? О. - Умножением, У. - Что на что умножим? О. - Скорость на время.. У. - Зная расстояние, которые проехал турист и что ему осталосьпроехать в 4 раза больше, что можем узнать? О. - Сколько км ему осталось проехать. У.- Каким действием? О. - Умножением У Что на что умножим? О. – Расстояние, которое проехал, умножим на 4. У. Зная, сколько км. турист проехал и сколько км ему осталось проехать. Что можем узнать? О. – Каков весь путь туриста. У. - Каким действием это узнаем? О. – сложение. У. – Что сложим? О. – Расстояние, которое турист проехал за 6 ч и расстояние, которое ему осталось проехать. Составим план решения задачи У. - Что узнаем в первом действии? О. - Расстояние, которое проехал турист за 6 ч. У. – Что узнаем во втором действии? О. – Сколько км ему осталось проехать. У. – Что узнаем в третьем действии? О. – Каков весь путь туриста. III этап. Решение задачи Назначение данного этапа - найти ответ на требование задачи, выполнив все действия в соответствии с планом. Для текстовых задач, решаемых арифметическим способом, используются следующие формы записи решения задачи: -запись решения по действиям с пояснением или без пояснения -запись решения с вопросами - запись решения в виде выражения -запись решения с пунктами плана Приведем примеры различных форм записи решения задачи о туристе
Если пояснения даются в устной форме (или совсем не даются), то запись будет следующей: 1)56* 6 =336 (км) 2)336*4=1344{ю*) 3)336+ 1344 = 1680 (км) 2. Запись решения по действиям с вопросами:
3. Запись решения в виде выражения. Запись решения в этой форме осуществляется поэтапно. Сначала записываются отдельные шаги в соответствии с планом затем составляется выражение и находится его значение. Это значение записывают, поставив после числового выражения знак равенства Вся запись становится числовым равенством в левой части которого - выражение, составленное по условию задачи, а в правой - его . значение, оно-то и позволяет сделать вывод о выполнении требований задачи. Так, для рассматриваемой задачи эта форма записи имеет вид: 56* 6 (км)- расстояние, которое проехал турист на поезде за 6 ч 56 * 6 * 4 (км) - расстояние, которое осталось проехать туристу. 56 * 6 + 56 * 4 (км) - путь, который должен проехать турист Пояснения к действиям можно не записывать, а давать их в устной форме, тогда запись решения задачи примет вид: 56 * 6 + 56* 6* 4 =1680 (км). IV этап. Проверка ренинам задачи. Приемы проверки решения задачи: 1. Прикидка. Суть приема: границы правильного ответа задачи прогнозируются до ее решения. Задача: « Водном куске 5 м ткани, в другом 7 м такой же ткани. Сколько стоит каждый кусок, если за оба куска уплатили 36 рублей» До решения задачи мы можем сказать, что каждый кусок будет стоить меньше, чем 36 рублей и второй кусок будет дороже первого. Если при решении задачи у нас получится, что второй кусок дешевле первого, или хотя бы один кусок дороже чем 36 рублей, то задача решена неверно. 2. Соотнесение полученного результата и условия задачи. Суть приема: найденный ответ вводится в текст задачи и на основе рассуждений устанавливается, не возникает ли при этом противоречия с каким-нибудь отношением. Проверим правильность решения задачи о туристе. Зная, что за б ч он проехал 336 км и, зная, что весь путь 1680 км, узнаем, сколько км ему осталось проехать 1680 — 336 - 1344 км. Согласно условию задачи это расстояние должно быть в 4 раза больше, чем 336 км. Проверим это 1344 : 336 = 4. Противоречия с условием задачи нет. Задача решена верно. 3. Решение задачи различными способами. Если при решении задачи другом способом или другим методом получается такой же ответ, то делается вывод, что задача была решена, верно. 4. Решение обратной задачи. Задача называется обратной для данной простой задачи, если: - то, о чем спрашивается в данной задаче, в обратной задаче становится известным, и - одно из того, что известно в данной задаче, в обратной надо узнать. Работа над задачей в начальной школе. I. Ознакомление с содержанием задачи. 1. Вопросы по тексту задачи. - Читаем задачу по себя - Кто прочитает задачу в слух? - О чем? О ком говорится в задаче? - Что они делали? - Что известно в задаче?; Что еще известно?, (условие). - Какой главный вопрос задачи?. 2. Запишем задачу кратко. - Какие слова помогут записать задачу кратко? - (О каких величинах говорится в задаче?) - Что означает число…….? (так спрашиваем о каждом числе) - Известно ли, сколько кг. привезли в среду? (так спрашиваем о каждом числе, которое неизвестно). О. Нет - Как обозначим? О. - ? кг. - А что известно о массе овощей привезенных в среду? О. Что привезли в 2 раза меньше, чем во вторник. (учитель пишет в 2 р меньше) - Какой главный вопрос задачи? 3. Кто повторит задачу по краткой записи? II. Поиск плана решения задачи. Разбор задачи
– Что спрашивается в задаче? - Можем ли это сразу узнать? О. Нет - Почему? - А можем ли сразу узнать сколько. …? О. Да Почему?
- Что узнаем в начале? - Каким действием? - Что на что умножаем? (ответ словами) - Что узнаем затем? - Каким действием? III. Решение задачи - Кто запишет решение задачи по действиям с пояснением. - Кто запишет решение задачи – выражением и ответ? |
