Оптимизация распределения усилий в строительных конструкциях. кр3 (Авто. Задача Требуется определить оптимальное сечение центральнорастянутого стального элемента. Характеристики исследуемого элемента длина l7м, продольное усилие n 700 кН, расчетное сопротивление стали R
 Скачать 53.39 Kb. Скачать 53.39 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования «Южно-Уральский государственный университет (Национальный исследовательский университет)» Институт открытого и дистанционного образования Кафедра «Техника, технологии и строительство» Оптимизация распределения усилий в строительных конструкциях КОтрольная работа №1 ЮУрГУ – 08.03.01.2022.77. РГР Вариант №7
Челябинск 2022 Задача 1. Требуется определить оптимальное сечение центрально-растянутого стального элемента. Характеристики исследуемого элемента: длина l=7м, продольное усилие N = 700 кН, расчетное сопротивление стали Ry=520-640 Мпа, коэффициент условия работы yc = 1.0; сечение постоянно по длине элемента ЕА = const. Первый этап – анализ центрально-растянутого стального элемента. 1 шаг – определить границы элемента.  Рис.1 Расчетная схема центрально-растянутого элемента 2 шаг – выбрать критерий оптимальности. За критерий оптимальности принимаем массу (М) центрально-растянутого элемента. 3 шаг – определить общее число независимых параметров, влияющих на величину критерия оптимальности, провести их ранжирование по степени влияния на величину критерия оптимальности. Масса элемента определяется произведением длины элемента, площади сечения и удельного веса: M=A*l*p. (1) В выражении (1) длина элемента l и удельный вес стали p величины постоянные, т.е. l = 7 м = const (по условию задачи), p = 7850 кГ/м3 = const. Поэтому независимой переменной является площадь поперечного сечения элемента А. Таким образом уравнение (1) имеет один независимый параметр А. 4 шаг – составить уравнение целевой функции. Сначала представим описание некоторой основной величины F в её зависимости от управляемых и неуправляемых параметров: F = (x1; с1,…,с6) (2) где управляемый параметр (независимый параметр) х1 – площадь поперечного сечения растянутого элемента А; неуправляемые параметры: с1 – расчетное сопротивление стали Ry = 520-640; с2 – коэффициент условия работы yc = 1.0 c3 – длина элемента l = 7м с4 – удельный вес стали p = 7850 кГ/м3 с5 – предельная гибкость  =400 =400с6 – усилие в стержне N = 700 кН Можно записать уравнение целевой функции:  (3) (3)5 шаг составить неравенства-ограничения. Условие прочности Условие жесткости 6 шаг – составить уравнения состояния – уравнения состояния составлять не нужно так как задача статистически определима. Второй этап решения задачи. 7 шаг – провести анализ целевой функции и неравенств- ограничений. Целевая функция (3) представляет собой уравнение с одним неизвестным (А). Условие прочности (4) представлено одним неизвестным (А). Условие жесткости (5) представлено неравенством с одним неизвестным (imin), т.е. рассматриваемая задача относится к линейному программированию. 8 шаг – выбрать метод решения задачи линейного программирования. Так как задача с одним неизвестным, то решение задачи сводится к решению линейного уравнения с одним неизвестным. Проведем некоторые упрощения. Из условий прочности (4) и жесткости (5) определяем требуемые величины площади поперечного сечения и минимального радиуса инерции сечения стержня: 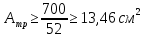 (6) (6)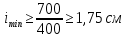 (7) (7)Так как подразумевается, что мы имеем в базе данных сокращенный сортамент стальных элементов, то выбираем профиль с наименьшим поперечным сечением. Однако, учитывая большую величину коэффициента градации сортамента, почти невозможно найти сечение стержня с характеристиками А = 13,46 см 2 и imin = 1,75 см (фактический экстремум в практических задачах чаще всего не совпадает с математическим). Поэтому решение задачи (минимум целевой функции) для разных видов поперечных сечений стержня минимальной массы будет находиться в области допустимых решений. За окончательное решение принимаем сечение с характеристиками приближенными по величине к требуемым (т. М [А = 12 см 2 и imin = 1,22 см]) Таблица 1 - Результаты решения задачи оптимизации
Вывод: Для требуемого элемента оптимальным сечением из условия минимальной массы будет сечение из двутавра №10. Задача №2. Определить оптимальное сечение центрально-растянутого элемента из стали различных марок, приняв диапазон расчетных характеристик материала от 520 до 640 МПа. Характеристики исследуемого элемента: длина l =7 м, продольное усилие N = 700КН, коэффициент условия работы с =1,0; поперечное сечение постоянно по длине элемента (ЕА = const); 520МПа < Ry < 640 МПа. Первый этап решения задачи - анализ центрально-растянутого стального элемента. 1 шаг - определить границы элемента. Границы элемента представлены на рисунке 1. 2 шаг - выбрать критерий оптимальности. За критерий оптимальности принимаем массу центрально-растянутого элемента. 3 шаг - определить общее число независимых параметров, влияющих на величину критерия оптимальности, провести их ранжирование по степени влияния на величину критерия оптимальности. Масса элемента определяется произведением длины элемента, площади сечения и удельного веса. В этом выражении независимым параметром является площадь поперечного сечения элемента А, которая зависит от марки стали, т.е. от величины расчетного сопротивления R. Мы имеем два независимых параметра. Произведем ранжирование независимых параметров. Величина площади сечения (А) при N = const зависит от расчетного сопротивления стали (марки стали). Чем оно выше, тем меньше площадь поперечного сечения растянутого элемента. Таким образом, для центрально-растянутого элемента основным неизвестным является расчетное сопротивление стали. За первый неизвестный параметр принимаем расчетное сопротивление стали, за второй - площадь поперечного сечения: Мы получаем задачу с двумя независимыми параметрами. 4 шаг - составить уравнение целевой функции. Сначала представим описание некоторой основной величины F в ее зависимости от управляемых и неуправляемых параметров: где управляемые параметры (независимые параметры): x 1 - расчетное сопротивление стали; x 2 - площадь поперечного сечения растянутого элемента; неуправляемые параметры (параметры, значения которых не подлежат изменению в рамках задачи): с1 - коэффициент условия работы с 1,0; с2 - длина элемента = 7 м; с3 - удельный вес стали = 7850 кГ/м3 ; с4 - предельная гибкость [ ] = 400. Для данной задачи, уравнение целевой функции: F M A min (10) 5 шаг - составить неравенства-ограничения. Условие прочности: Условие жесткости 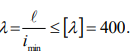 (12) (12)Расчетное сопротивление 520МПа < Ry < 640 МПа. (13) 6 шаг - составить уравнения состояния - уравнения состояния составлять не нужно, так как задача статически определима. Второй этап решения задачи. Для решения математической задачи оптимизации необходимо выполнить: 7 шаг - провести анализ целевой функции и неравенств-ограничений. Целевая функция (10) представляет собой уравнение с одним неизвестным (А). Условие прочности (11) представлено неравенством с двумя неизвестными (A, R). Условие жесткости (12) представлено неравенством с одним неизвестным (imin). Проведем некоторые упрощения в уравнении функции цели (10) с учетом ограничений:  (14) (14)Неизвестный параметр в уравнении функции цели находится в знаменателе, поэтому задача относится к нелинейному программированию. 8 шаг - выбрать метод решения задачи линейного программирования. Так как в 7-м шаге мы выявили зависимость переменных А и R, то получили уравнение функции цели с одним неизвестным. Поэтому решение данной задачи сводится к решению линейного уравнения (14) с одним неизвестным, но в нелинейной постановке. Представим ограничений (11) и (13) графически (рисунок. 3). При этом с учетом ограничений (13) определим минимальные значения площади сечения растянутого элемента:  (15) (15)Таким образом, мы получили область допустимых решений, ограниченную прямыми: Аmin = 700/64=10.9 см2 ; Ry≤640 Мпа ; Ry≥520 и кривой А≥N / Ryyc По сортаменту подбираем профиль, площадь которого (A) и минимальный радиус инерции удовлетворяет требованию минимальной массы элемента, т.е. удовлетворяет уравнению целевой функции. Таблица 2 – Результаты решения задачи оптимизации
Вывод: Оптимальным решением (с учетом существующего сортамента) является стержень из круглой трубы 76*4,5 мм с площадью сечения А = 10,11 см2, выполненный из стали с расчетным сопротивлением 520 МПа. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
