прикладні задачі квадратні рівняння. Задача у шаховому турнірі було зіграно 66 партій. Знай діть кількість учасників турніру, коли відомо, що кожний
 Скачать 101.5 Kb. Скачать 101.5 Kb.
|
|
Розв′язування задач за допомогою квадратних рівнянь Задача 1. У шаховому турнірі було зіграно 66 партій. Знайдіть кількість учасників турніру, коли відомо, що кожний учасник зіграв з кожним по одній партії. Розв'язання: Нехай х – число учасників турніру. Кожний зіграв (х-1) партію, всього х(х-1) партій. Учасники грають парами, значить, було зіграно Відповідь: 12 учасників турніру. Задача 2. На весь шлях автомобіль витратив 3 год., причому останні 240 км він проїхав зі швидкістю на 20 км/год. більшою, ніж перші 100 км. Знайти швидкість автомобіля, з якою він проїхав останні 240 км. Розв'язання: Нехай х км/год. – швидкість автомобіля, з якою він їхав перші 100 км, тоді (х+20) км/год. – швидкість автомобіля на останніх 240 км. За умовою задачі на весь шлях автомобіль витратив 3 год. Складаємо і розв'яжемо рівняння. Відповідь: 120 км/год. Розв'яжи ребус зображений на малюнкові. (8 сх.) 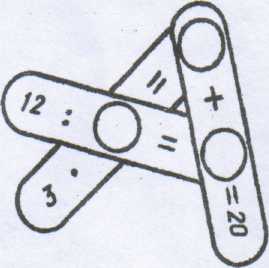 Розв'язання: Треба знайти три числа такі, щоб добуток першого і числа 3 дорівнював другому числу; сума другого і третього чисел дорівнювала б 20; відношення числа 12 до першого числа дорівнювало б третьому числу. Нехай х – перше число, тоді Зх – друге число, 20 – Зх – третє. Складаємо рівняння: Розв'яжемо це рівняння. Якщо х = 6, то Зх=18 і 20 – 18 = 2; Якщо До дробових раціональних рівнянь приводить велика кількість задач на рух та спільну роботу. Задача 1 (на рух). Теплохід пройшов течією річки 150 км і повернувся назад, витративши на весь шлях 5,5 години. Знайдіть швидкість течії річки, якщо швидкість теплохода в стоячій воді 55 км/год. Розв′язання
Нехай швидкість течії річки х км/год. Тоді за течією теплохід рухався зі швидкістю (55 + х) км/год і пройшов 150 км за ..... Задача 2 (на сумісну роботу ) Дві бригади, працюючи разом, виконали певне завдання за 4 дні. Скільки днів потрібно на виконання цієї роботи кожній бригаді окремо, якщо першій бригаді для цього потрібно на 6 днів менше, ніж другій? Розв'язання. Нехай перша бригада може виконати це завдання за х днів.Тоді другій потрібно ...... Відповідь: першій бригаді потрібно 6 днів, другій — 12 днів. Отже, наскільки ви компетентні щодо розв’язання квадратних рівнянь, і будемо з’ясовувати. Поділимо наш клас на три групи , а в кожній групі кожен учень вибере собі професію (використаю капелюхи чотирьох кольорів ,а учні виберуть, який капелюх до вподоби ). Таким чином утвориться 3 групи,в кожній з груп буде: практик (червоний капелюх), архітектор (синій), економіст (білий), дизайнер (зелений). Кожна група буде виконувати своє завдання ,але кожен відповідатиме за своє: 1)«Дизайнери» - повинні розробити та намалювати ескізи до задач; 2) «Практики» - знайти інформацію щодо будівництва (які матеріали потрібні та їх кількість); 3) «Економісти» - проаналізувати ринок будівельних матеріалів та підрахувати за даними «практиків» вартість матеріалів; 4) «Архітектори» - провести відповідні розрахунки. В кінці уроку групи презентують звіт. Наше з вами завдання навчитись застосовувати математичні знання у практичних сферах людської діяльності та навчитись працювати колективно. І етап проходить під девізом «Хай живе теорія!» Мета цього етапу уроку: актуалізація опорних знань з теоретичного матеріалу. Для виконання домашнього завдання було запропоновано самостійно знайти цікаву та корисну інформацію з теми, яку вивчаємо. У нас є такі учні, які склали або доповідь, або реферат. Учні роблять повідомлення про свою роботу. Перший учень Необхідність розв’язувати рівняння не тільки першого, а й другого степеня ще в давнину була обумовлена потребою розв’язати задачі, пов’язані із знаходженням площ земельних ділянок, із земляними роботами військового характеру, з розвитком астрономії і самої математики. Квадратні рівняння уміти розв’язувати близько 2000 років до н.е. вавилоняни. Застосовуючи сучасну алгебраїчну символіку, можна сказати, що в їх клинописних текстах трапляються такі квадратні рівняння: х2 + х = 0,75; х2 - х = 14,5. Хоча рівень розвитку алгебри у Вавилоні був високим, проте у клинописних текстах поняття від’ємного числа, а також загальні методи розв’язування квадратних рівнянь відсутні. Другий учень Квадратні рівняння цікавили й Діофанта. Попри те, що в «Арифметиці» Діофанта немає систематичного викладу алгебри, у ній міститься систематизований ряд задач, що розв’язуються за допомогою складання квадратних рівнянь. Наприклад, рівняння з «Арифметики» Діофанта: 12 х2 + х = 1; 630х2 +73 х = 6. Задачі на квадратні рівняння зустрічаються вже в астрономічному тракті «Аріабхаттіам», складеному в 499 р. індійським математиком і астрономом Аріабхаттою. Інший індійський учений, Бахмагупта (VI ст.), виклав загальне правило розв’язування квадратних рівнянь, зведених до єдиної канонічної форми: ах2+bx = c, а>0. Правило Брахмагупти по суті збігається з нашим. Третій учень В алгебраїчному трактаті аль -Хорезмі дається класифікація лінійних і квадратних рівнянь. Автор нараховує 6 видів рівнянь: 1. Квадрати, що дорівнюють кореням, тощо ах2 = bx. 2. Квадрати, що дорівнюють числу, тобто ах2 = с. 3. Корені, що дорівнюють числу, тобто ах = с. 4. Квадратні числа, що дорівнюють кореням, тобто ах2+с = bx. 5. Квадрати і корені, що дорівнюють числу, тобто ах2+bx = с. 6. Корені і числа, що дорівнюють квадратам, тобто bx + с = ах2 Трактат аль-Хорезмі є першою книжкою, що дійшла до нас, в якій систематично викладено класифікацію квадратних рівнянь і подано формули їх розв’язування. Четвертий учень Формули розв’язування квадратних рівнянь в Європі були вперше викладені у «книзі абака» італійського математика Леонардо Фібоначчі в 1202 р. Загальне правило розв’язування квадратних рівнянь виду х2+bx = с при всіх можливих комбінаціях знаків коефіцієнтів b і с було сформульовано в Європі лише в1544 р. М. Штизелем. Розв’язуванням квадратних рівнянь займалися Вієт, Тарталья, Бомбеллі. Лише в Х VIІ ст. завдяки роботам Жирара, Декарта, Ньютона та інших учених спосіб розв’язування квадратних рівнянь набуває сучасного виду. ІІ етап. Цікавинки навчання. 1. Процес, який відбувається під час утворення льоду і снігу. (Кристалізація). 2. Автор слів: «Хімія – права рука фізики, а математика – її очі». (Ломоносов). 3. Про яку науку відомий фізик Макс Планк сказав: „Ніяка інша наука не може зрівнятися з нею, особлива чарівність якої є наслідком краси її будови,... розвиток якої є наслідком розв’язування питань природознавства”? (Математика). 4. Видатний вчений-інженер, конструктор найзнаменитішого (суцільнометалевого) моста в Києві. (Патон). 5. Цей процес лежить в основі виробництва сталі, чавуну, інших сплавів, використовується при електрозварюванні металів. (Плавлення). 6. Рівність, яка містить невідомі числа, позначені буквами. (Рівняння). Висновок. З’ясували всі теоретичні питання, готові до наступного етапу. ІІІ етап. «Практика – велика справа» Зараз пропоную кожній групі задачу. Задача 1. Іван Петрович розпочав будівництво будинку на ділянці землі , що має форму прямокутника. Одна сторона ділянки на 16 м менша від іншої, а її площа дорівнює 720 м2. Допоможіть Івану Петровичу здійснити необхідні розрахунки: Знайдіть периметр ділянки. Для початку будівництва уздовж стін ділянки потрібно покласти піно блоки. Скільки штук піно блоків потрібно придбати Івану Петровичу для будівництва будинку , якщо довжина одного такого блоку дорівнює 4 м. Для придбання піно блоків Іван Петрович має звернутися до трьох постачальників, умови яких подано в таблиці.
Яка пропозиція покупки з доставкою буде найвигіднішою для Івана Петровича? Задача 2. Поряд з будинком де мешкає Іван Петрович , установили спортивний майданчик прямокутної форми, площа якого 112 м2. Обчисліть розміри майданчика, якщо його довжина на 6 м більша за ширину. Для виготовлення водостоку необхідно закупити швелер, довжина якого має бути на півметра довшою за необхідну довжину виробу. Обчисліть вартість швелера для виготовлення водостоку по одній зовнішній стороні спортмайданчика , якщо погонний метр швелера коштує 140 грн. Огорожу спортивного майданчика виготовлено із секційного паркану, висота секції якого дорівнює 2,5 метра, а ширина – 2 м. Обчисліть вартість матеріалу для паркану , якщо вартість секції становить 250 грн. Поблизу дома Івана Петровича знаходиться дитячий майданчик. Задача 3. На дитячому майданчику установили нову дитячу гірку – споруду з гладким спуском і драбиною, яка дозволяє забиратися на верхню площадку , щоб потім скочуватися вниз. Площадка для спуску розташована на висоті 1,5 м. Розрахуйте довжину похилого спуску , якщо він на півметра довший за його проекції. Скільки метрів проїхав за день Василько, якщо він спустився 18 разів? А кілометрів ? Знайдіть площу поверхні спуску, якщо його ширина -70 см. Розрахуйте довжину драбинки , якщо вона на 90 см. довша за її проекцію. Обчисліть вартість матеріалу для спуску ,якщо 1м2 заліза коштує 200грн. Розрахуйте висоту сходинок, якщо встановлено 7 сходинок і перша розміщується на висоті 30 см. від поверхні землі. IV. Домашнє завдання. Ми повинні дбати про навколишнє середовище. Дома вам потрібно розв’язати таку задачу: 1 га лісу за рік поглинає 9,32 т вуглекислого газу і виділяє 7,2 т кисню, який забезпечує дихання 200 чоловік. Скільки потрібно кисню для дихання вашій сім’ї на рік та скільки потрібно посадити лісу для вашої сім’ї? Скільки вуглекислого газу поглине цей ліс? Працюючи разом, маючи поруч надійних партнерів, ви досягли успіху. V. Аналіз уроку учнями. Саме час повернутися до початку уроку – до мети, яку ми перед собою ставили. Поміркуйте, чи досягли ви її. Чи систематизували знання про квадратне рівняння та способи його розв’язування, чи перевірили свої навчальні досягнення під час виконання завдань? Крім того, треба дати відповідь на запитання: «Що допомогло нам досягти успіху?» Уміння аналізувати є дуже важливим у наш насичений інформацією час. Людиною, яка вміє аналізувати, практично ніколи неможливо маніпулювати, вона завжди знайде вихід з будь-якої ситуації. Для аналізу уроку клас розділяю на чотири групи( по капелюхах) Кожна група одержує картку з запитаннями. В групах обговорюють запитання і один учень, з кожної групи робить висновки. Картка 1. 1. Яка тема даного уроку? 2. Які знання, вміння було відтворено на початку уроку? 3. Які нові знання отримали на уроці? 4. Які методи роботи на уроці використовувалися? 5. Чи всі учні на уроці працювали? 6. Чи отримали на уроці домашнє завдання? Чи різне воно для учнів залежно від рівнів їх досягнень? Картка 2 1. У якому настрої ви перебували на уроці? (Доброму, поганому, хвилювалися, боялися, сумували, були зацікавлені, замкнені, інше). 2. У якому настрої на вашу думку перебували інші учні класу? 3. Яким був настрій у вашого вчителя? 4. На розвиток яких здібностей вплинув цей урок? (Мислення, пам’ять, уваги, вміння бути дисциплінованим, самостійним, спостережливим тощо).9 Картка 3. 1. Що на даному уроці заважало вам працювати продуктивно, успішно? (Відсутність знань, досвіду, неуважність, недисциплінованість тощо). 2. Що заважало іншим учням, учителю? 3. Що було непотрібним, зайвим? Які негативні елементи на уроці ви помітили? Картка 4. 1. Що корисного для навчання, для подальшого життя ви винесли з уроку? (Училися самостійно працювати, досягати успіху, допомагати іншим, спілкуватися, тощо). 2. Чому можемо сказати, що цей урок важливий для вас? 3. Де, у яких ситуаціях ви можете використовувати набутий на уроці досвід? Думаю, уміння аналізувати ситуації ще не раз стане вам у нагоді. Усе людське життя – це не що інше, як постійне визначення мети та бажання досягнення успіху під час розв’язування все нових знань та проблем. Учіть свій розум та душу бачити добро, і тоді дорога до успіху буде вам відкрита |
