Задача 1. Задача Вариант 19. 8 Тело m массы m скользит без трения вдоль горизонтальной оси Ox под
 Скачать 68.89 Kb. Скачать 68.89 Kb.
|
 Рисунок 1.1 Рисунок 1.1Задача 1. Вариант 19.8 Тело M массы m скользит без трения вдоль горизонтальной оси Ox под действием трех сил: возвращающей силы зависящей от координаты  =-3.6*x* =-3.6*x*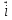 (H), силы сопротивления среды (H), силы сопротивления среды  =-1.8* =-1.8*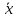 * *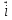 (H) и силы (H) и силы  =1.5* =1.5* * *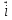 (H), зависящей от времени. Найти уравнение движения тела, (H), зависящей от времени. Найти уравнение движения тела, если заданы её начальная скорость  и её начальная абсцисса и её начальная абсцисса  . .Дано: m=0.9кг,  =-3.6*x* =-3.6*x*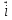 (H), (H), =-1.8* =-1.8*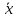 * *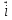 (H), (H), =1.5* =1.5* * *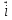 (H), (H),  =0.1м, =0.1м,  = = =0.5м/c. =0.5м/c.Определить: x=x(  )-? )-?Решение. 1.Примем тело M за материальную точку M. Рассмотрим материальную точку М массы m, начинающую движение с начальной скоростью  (рис.1.1). (рис.1.1). 2.Определим движение точки М, считая, что на нее действует силы:  , ,  , , , ,  , ,  . .3. Возьмем начало координат в точке O, ось Ox направим вправо. 4.Составим дифференциальное уравнение, описывающее движение точки M в проекции на ось Ox: m* 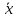 =1.5* =1.5* -3.6*x-1.8* -3.6*x-1.8*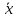 ; ;0.9* 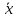 =1.5* =1.5* -3.6*x-1.8* -3.6*x-1.8*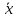 ; ;Или: 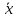 =(5/3)* =(5/3)* -4*x-2* -4*x-2*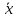 ; (1) ; (1)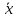 +2* +2*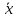 +4*x=(5/3)* +4*x=(5/3)* ; (2) ; (2)Решение линейного дифференциального уравнения второго порядка (2) представим в виде: x=  * * *sin( *sin( * * )+ )+ * * *cos( *cos( * * )+5* )+5* /21; /21;x=  * * *sin(1.732* *sin(1.732* )+ )+ * * *cos(1.732* *cos(1.732* )+0.238* )+0.238* ; ;Скорость этого движения: 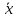 =- =- * * *sin(1.732* *sin(1.732* )+ )+ * * *cos(1.732* *cos(1.732* )*1.732- )*1.732- * * *cos(1.732* *cos(1.732* )- )--  * * *sin(1.732* *sin(1.732* )*1.732-0.774* )*1.732-0.774* ; ;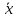 =- =- *( *( *sin(1.732* *sin(1.732* )- )- *cos(1.732* *cos(1.732* )*1.732)- )*1.732)- *( *( *cos(1.732* *cos(1.732* )+ )++  *sin(1.732* *sin(1.732* )*1.732)-0.774* )*1.732)-0.774* ; ;Подставляем начальные условия. При  =0, =0,  =0.1м, =0.1м,  = = =0.5м/c: =0.5м/c:0.1=  +0.238; (3) +0.238; (3)0.5=-  *(-1.732)- *(-1.732)- -0.774; (4) -0.774; (4) =0.1-0.238=-0.138; (5) =0.1-0.238=-0.138; (5) =(0.5+ =(0.5+ +0.774)/1.732=(0.5-0.138+0.774)/1.732=1.136/1.732=0.656; (6) +0.774)/1.732=(0.5-0.138+0.774)/1.732=1.136/1.732=0.656; (6)Уравнение относительного движения материальной точки М принимает вид: x=0.656*  *sin(1.732* *sin(1.732* )-0.138* )-0.138* *cos(1.732* *cos(1.732* )+0.238* )+0.238* ; ;Ответ: x(  )=0.656* )=0.656* *sin(1.732* *sin(1.732* )-0.138* )-0.138* *cos(1.732* *cos(1.732* )+0.238* )+0.238* . . |
