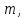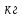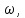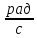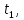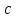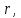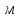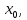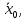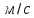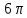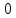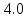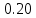Родионов_3215. Исследование относительного движения материальной точки Вариант 17 Схема движения тела а показана на рисунке Рисунок 1
 Скачать 429.95 Kb. Скачать 429.95 Kb.
|
|
Задание Д.4 Исследование относительного движения материальной точки Вариант 17 Схема движения тела А показана на рисунке 1. 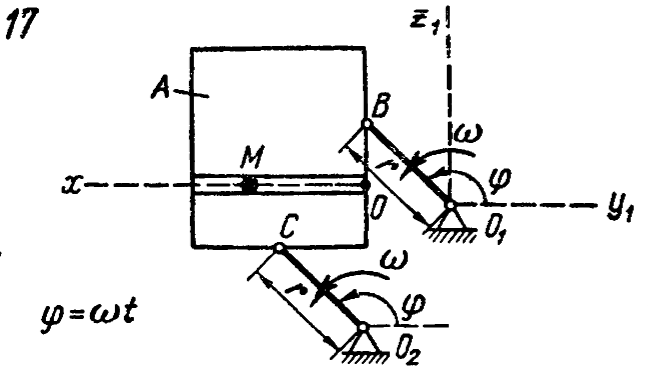 Рисунок 1 Необходимые для решения данные приведены в таблице 1. Таблица 1
Шарик М, рассматриваемый как материальная точка, перемещается по цилиндрическому каналу движущегося тела А, которое равномерно вращается вокруг неподвижной оси (рисунок1). Найти уравнение относительного движения этого шарика 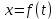 , приняв за начало отсчета точку О, а также координату х и давление шарика на стенку канала при заданного значении , приняв за начало отсчета точку О, а также координату х и давление шарика на стенку канала при заданного значении 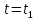 . .Решение Движение шарика является сложным. Относительное движение – движение вдоль трубки, переносное –движение трубки вместе телом А. Направим ось 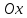 подвижной системы координат вдоль трубки, оси подвижной системы координат вдоль трубки, оси 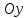 ей перпендикулярны. Начало подвижной системы координат совместим с точкой O, как предлагается в условии задания. На точку действуют две силы: сила тяжести ей перпендикулярны. Начало подвижной системы координат совместим с точкой O, как предлагается в условии задания. На точку действуют две силы: сила тяжести 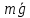 и реакция стенок трубки и реакция стенок трубки 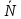 (рисунок 2). (рисунок 2).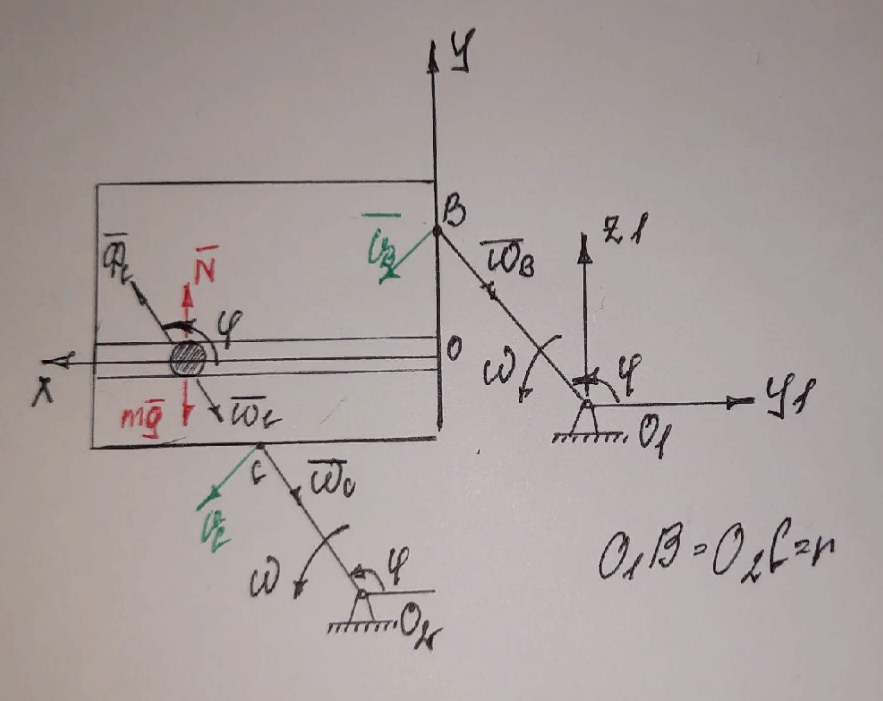 Рисунок 2 Для решения задачи воспользуемся дифференциальным уравнением относительного движения точки 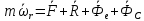 Т.к. переносное движение (движение тела А) является поступательным, то ускорение Кориолиса равно нулю, следовательно, кориолисова сила инерции 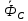 также равна нулю. также равна нулю. Т.к. тело А движется поступательно, то скорости и ускорения точек В и С равны, следовательно, переносное ускорение шарика М: 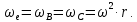 При поступательном переносном движении сила инерции будет одной и той же во всех точках подвижной системы отсчета. Она направлена в сторону, противоположную переносному ускорению 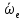 . .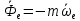 По модулю 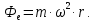 Дифференциальное уравнение относительного движения получает такой вид: 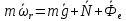 Спроектируем данное уравнение на оси подвижной системы координат 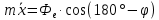 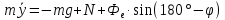 Учитывая, что 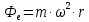 , , 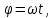 получим получим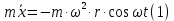 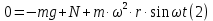 Начальные условия: при 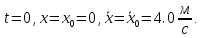 Решим уравнение (1): 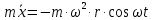 Разделим обе части уравнения на массу шарика m, получим: 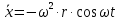 Мы получили дифференциальное уравнение второго порядка. Понизим порядок уравнения, выбрав за новую переменную скорость 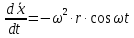 Разделим переменные и найдем соответствующий интеграл: 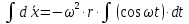 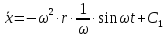 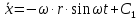 Постоянную 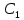 найдем из начальных условий и с помощью данных из таблицы 1: найдем из начальных условий и с помощью данных из таблицы 1: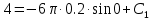 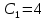 Запишем интеграл нашего уравнения 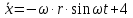 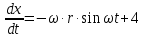 Повторно разделим переменные и найдем соответствующий интеграл: 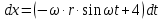 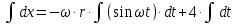 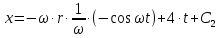 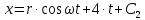 Постоянную 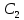 также найдем из начальных условий и с помощью данных из таблицы 1: также найдем из начальных условий и с помощью данных из таблицы 1: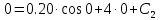 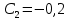 Запишем уравнение относительного движения точки: 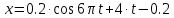 Окончательное уравнение относительного движения шарика М примет вид: 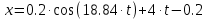 . .Найдем координату 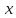 в момент времени в момент времени 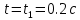 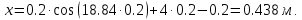 Из уравнения (2) найдем реакцию стенки трубки в момент времени 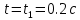 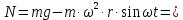 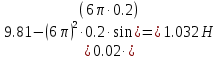 Искомое давление шарика М на стенки трубки по числовому значению равно найденной реакции Nи направлено в противоположную сторону. Ответ: 1) Уравнение относительного движения шарика М: 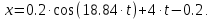 2) Координата х (при 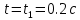 ): ):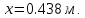 3) Давление шарика на стенку трубки (при 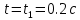 ): ):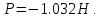 | ||||||||||||||||||