- -
Лекция 11. ГИДРО- И АЭРОДИНАМИКА.
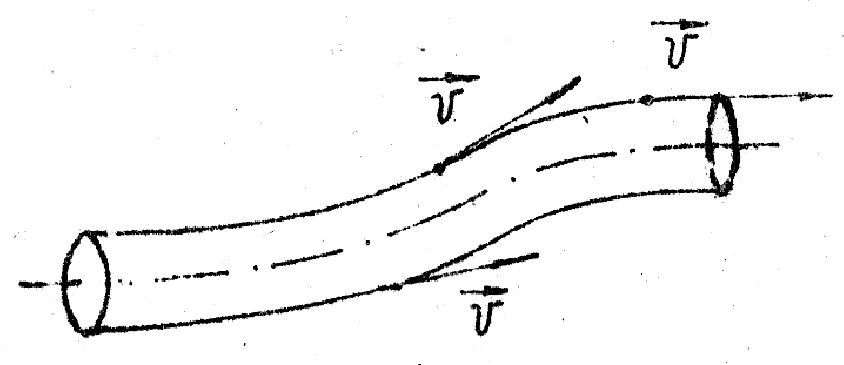
Гидро- и аэродинамика - раздел физики, занимающийся изучением законов движущихся жидкостей и газов. Законы движения жидкостей справедливы и для газов, если скорости потока газа оказывается меньше скорости звука, поскольку в этом случае газы можно считать несжимаемыми. Движение жидкостей происходит под действием сил тяжести, разности давлений, внешней силы и т.д. Скорость каждой частицы в потоке жидкости или газа в каждый момент времени имеет определённое направление и величину. Пространство, заполненное движущимися частицами, называется потоком. Для наглядного представления потока жидкости используются линии тока, касательные к которым в любой точке совпадают с направлением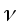 , т.е. определяют направление движения жидкости и совпадают с траекторией частиц. Часть жидкости, ограниченная линиями тока, называется трубкой тока (аналог трубы). В этом случае , т.е. определяют направление движения жидкости и совпадают с траекторией частиц. Часть жидкости, ограниченная линиями тока, называется трубкой тока (аналог трубы). В этом случае 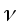 касательны к поверхности трубки, а частицы не пересекают её стенок. касательны к поверхности трубки, а частицы не пересекают её стенок.
Идеальной жидкостью (идеальный поток) называется такая жидкость, при рассмотрении движения которой можно пренебречь существованием внутреннего трения между слоями (частицами) и образованием вихрей при ее течении (движение каждой частицы осуществляется вдоль направления течения - это ламинарное течение).
Теорема о неразрывности струи. Уравнение Бернулли.
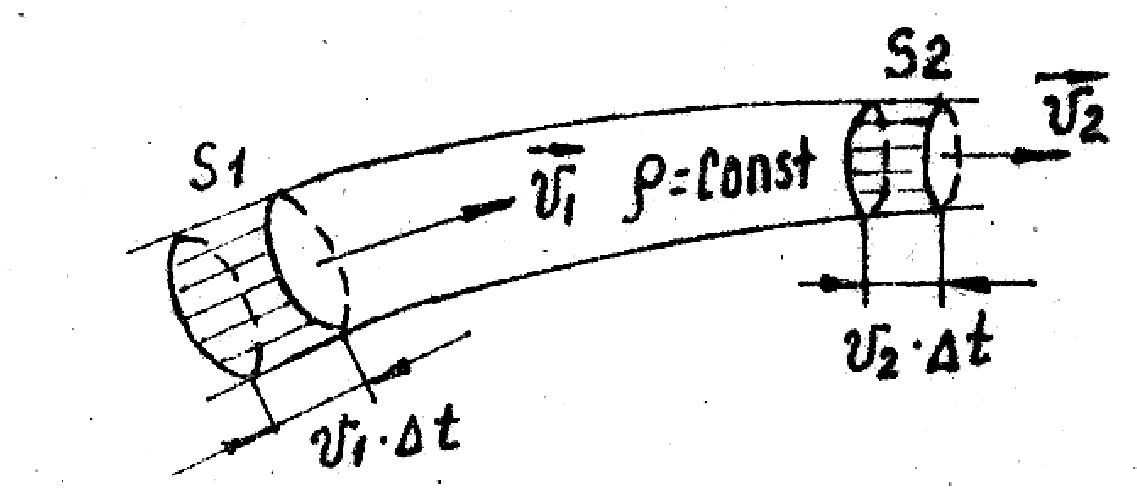
Дано: идеальная жидкость движется стационарно вдоль трубки тока.
Найти: поток вектора скорости Ф.
Выберем два произвольных сечения S1 и S2 перпендикулярных трубке тока, т.е. перпендикулярных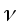 . Пусть . Пусть 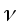 = Const, тогда за tчерез S1 пройдут все частицы жидкости из объёма V1 = S1t, а через S2 соответственно V2= S2t. Если трубка тока тонкая ( = Const, тогда за tчерез S1 пройдут все частицы жидкости из объёма V1 = S1t, а через S2 соответственно V2= S2t. Если трубка тока тонкая (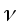 = Сonst), жидкость идеальная ( = Const) и t = Const, то 1 = 2 и S11 = S22 , т.е. объёмы жидкости, протекающие в единицу времени через сечения S1 и S2 равны Const или = Сonst), жидкость идеальная ( = Const) и t = Const, то 1 = 2 и S11 = S22 , т.е. объёмы жидкости, протекающие в единицу времени через сечения S1 и S2 равны Const или
S = Const.
Анализ:
1). Для несжимаемой (идеальной) жидкости при её стационарном сечении величина Sв любом сечении одной и той же трубки тока должна быть одинакова.
2). S11 = S22 - уравнение потока (уравнение непрерывности струи), т.е. Ф = Const.
3). При уменьшении S скорость () частицы должна возрастать, т.е. они должны двигаться с ускорением, которое создаётся разностью давлений вдоль оси трубки тока.
Давление в потоке движущейся жидкости состоит из статического (pст) и динамического (pдин). Первое обусловлено потенциальной энергией жидкости, находящейся под давлением. Второе (давление напора) обусловлено кинетической энергией движущейся жидкости.
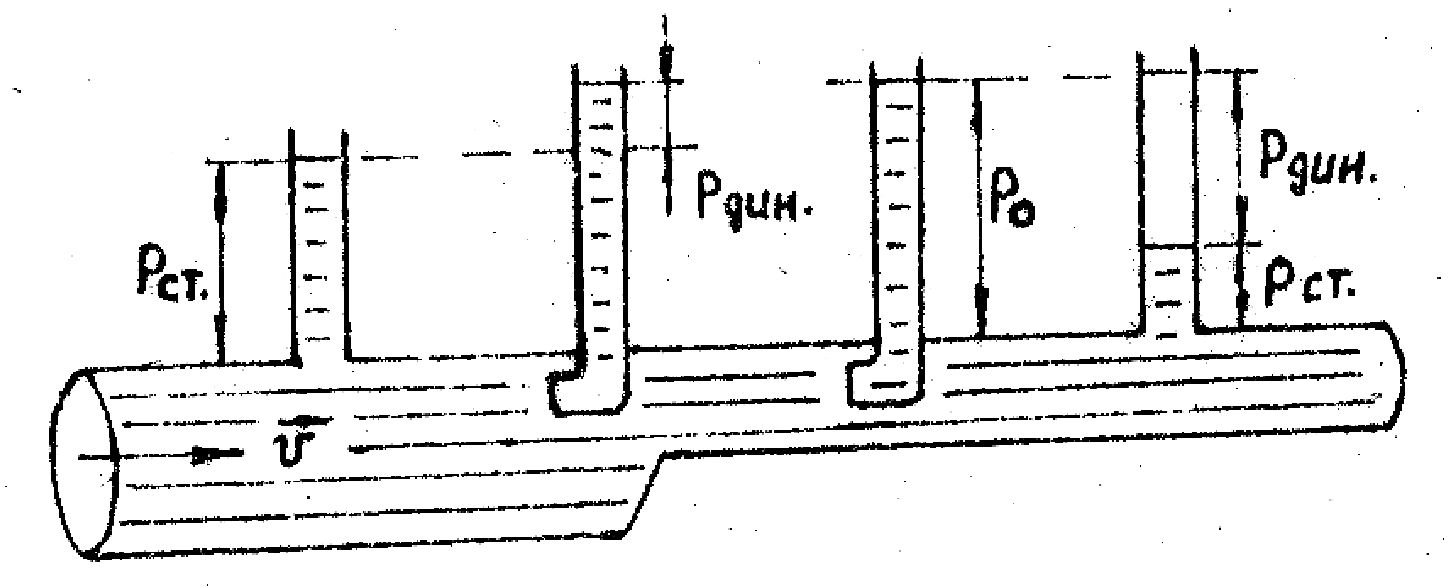
При увеличении скорости потока pдин - возрастает, а pст - уменьшается. В покоящейся жидкости pдин = 0, а p0 = pст , причём pст= p1 + p2 , где p1 = 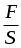 , p2 = gh. , p2 = gh.
Закон Бернулли. В стационарном потоке сумма статического и динамического давлений остаётся постоянной. Эта сумма соответствует гидростатическому давлению в покоящейся жидкости.
Если жидкость течёт в наклонной трубе, то следует учитывать изменение энергии, связанное с ее наклоном.

Дано: стандартно текущая идеальная жидкость по трубе переменного сечения и имеющей наклон. Движение жидкости осуществляется за счёт разности внешнего давления p1 > p2 .
Найти: уравнение движения жидкости.
В сечении S1 имеем: p1ст и 1, h1 , где h1 - высота этого сечения относительно произвольно выбранного уров-ня.
В сечении S2: p2ст и 2, h2. Кроме того, известна - (плотность) жидкости. Работа (A), расходуемая на изменение 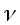 и h - жидкости, должна быть равна A= dW= dWкин + dWp . Здесь dWкин,, dWp - изменение, соответственно, кинетической и потенциальных энергий. и h - жидкости, должна быть равна A= dW= dWкин + dWp . Здесь dWкин,, dWp - изменение, соответственно, кинетической и потенциальных энергий.
A= 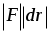
A = dW = FdS
Wk= 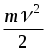
Wk= 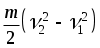
Wp= mgh
Wp= mg (h2 - h1)
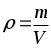
= Const
Для элемента dV: dW= FdS= pdV.
Так как жидкость идеальная, то V = Const,
(p1 - p2)V= mg(h2 - h1) + 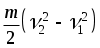 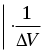
получим p1 - p2= gh2 - gh1 + 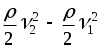 . .
Переносим, разделяя переменные, и получаем уравнение Бернулли
p1 +g h1 + 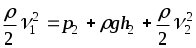 или или
p +g h + 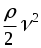 = Const = p0 . = Const = p0 .
Анализ:
1). Сумма pст (гидростатическое давление), обусловленного весом столба жидкости pст = gh, и pдин , обусловленногокинетической энергии жидкости, pдин = 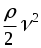 , остаётся постоянной p0 = Const вдоль всей линии тока. , остаётся постоянной p0 = Const вдоль всей линии тока.
2). Формула верна лишь для идеальных жидкостей, в которых отсутствует трение.
3). Если h = Const, т.е. жидкость течёт по прямой трубе, то
p1 + 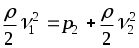
или p + 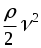 = p0 = Const. = p0 = Const.
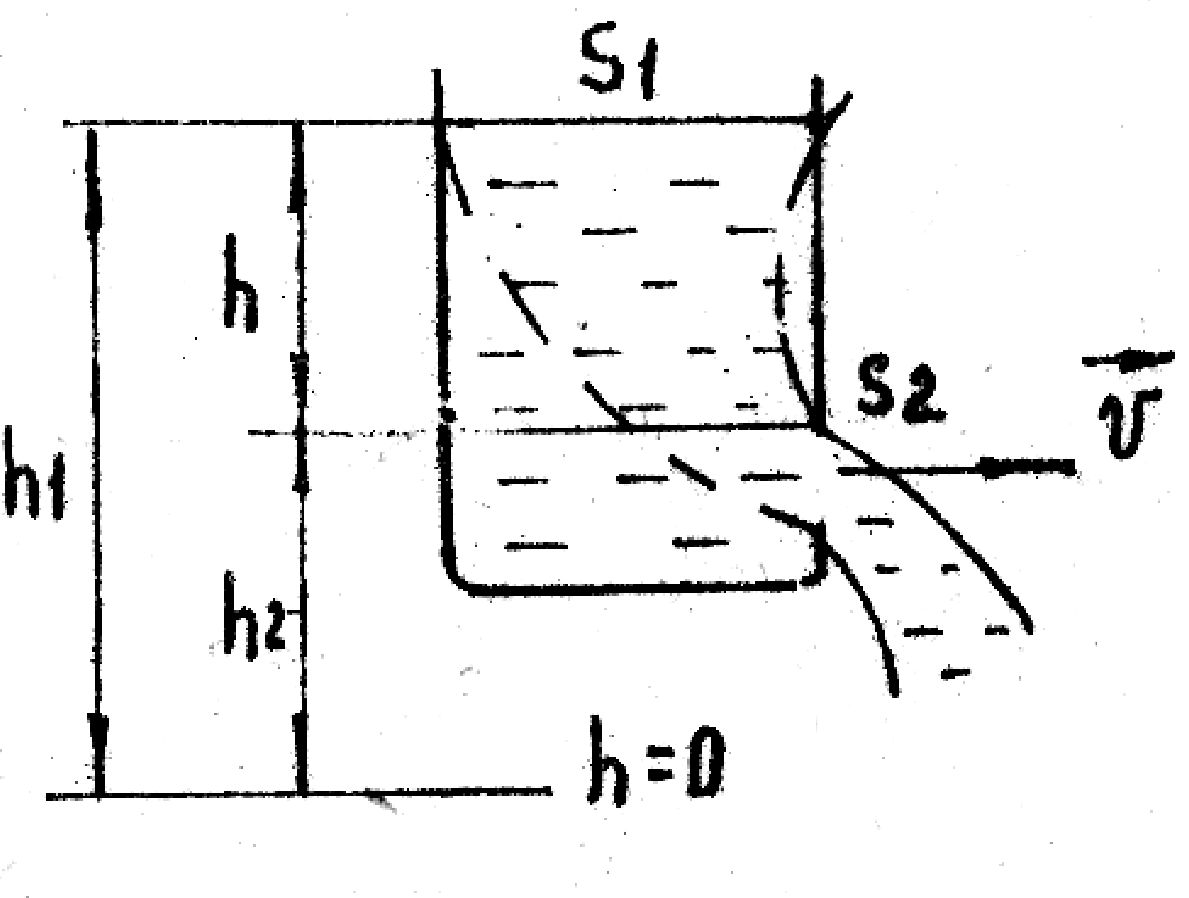
4). Жидкость вытекает из отверстия в широком сосуде со скоростью  . Выделим в жидкости трубку тока с сечениями S1 и S2. Используем уравнение Бернулли: . Выделим в жидкости трубку тока с сечениями S1 и S2. Используем уравнение Бернулли:
p1+gh1+  , ,
p1 = p2 = pатм
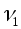 в сечении в сечении
S1 = 0
h = h1 - h2
в которое подставим наши условия.
Получим gh1 = 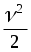 + gh2 или + gh2 или 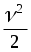 = gh. = gh.
Отсюда = 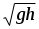 . .
Из полученного следует:
а). Скорость истечения жидкости из отверстия, расположенного на глубине h открытой поверхности, совпадает по величине со скоростью свободного падения тела с высоты h.
б). Скорость истечения реальных жидкостей зависит от формы отверстия. Коэффициент, который её учитывает, называется коэффициентом истечения ( ), причём < 1.
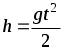 t - 0 = at t - 0 = at
t2 - 0 2 = 2aS
2 = 2gh
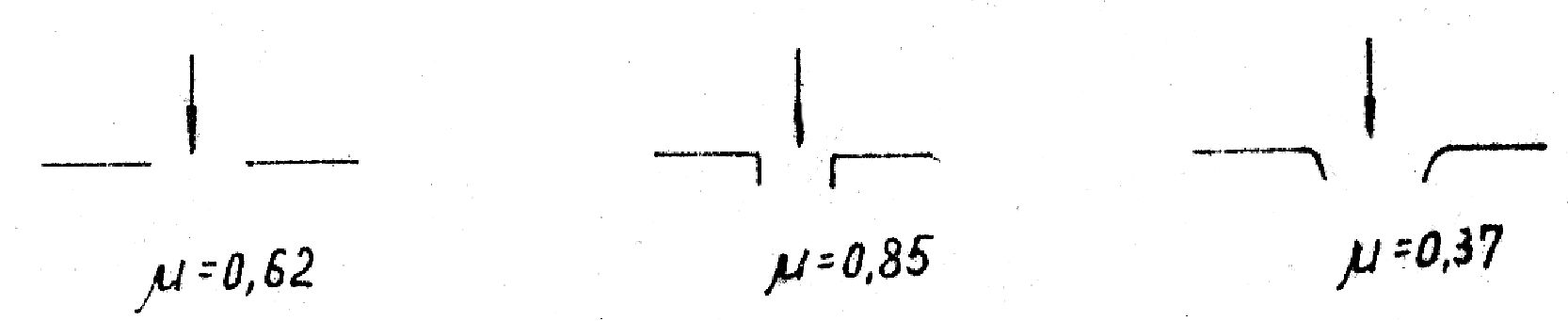
V = S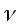 - вы- - вы-
текающий объём
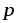 = m = m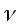
m= V
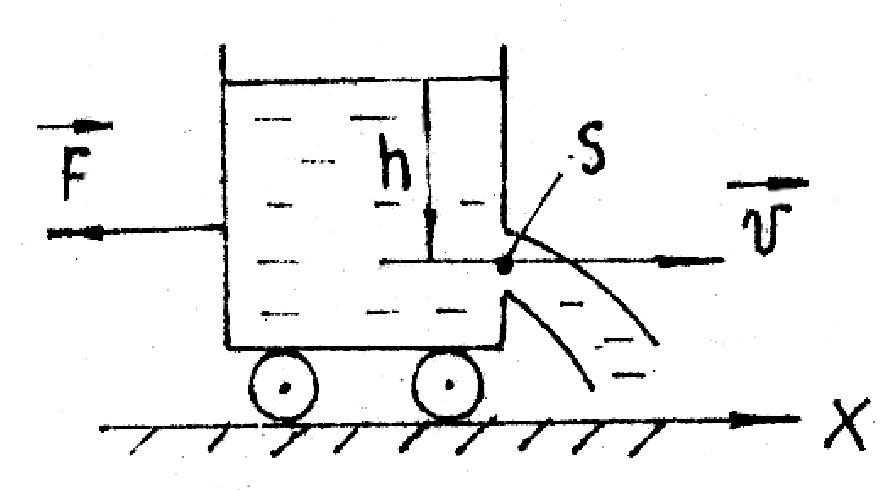
5). Если жидкость вытекает из отверстия в широком сосуде способном двигаться, то за время t изменение импульса
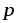 = S = S 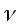 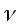 t . t .
Сам сосуд получает от жидкости 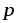 , т.е. , т.е.
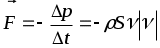 . .
Это сила реакции вытекающей струи. Знак () указывает направление движения сосуда. Для  с учётом подстановки с учётом подстановки 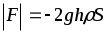 , ,
где 2 = 2gh
Из полученного следует:
а). Логично предположить, что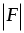 должна быть равна силе гидростатического давления F2 = ghS (см. лекция 10, раздел 10.5), но реальная сила в 2 - раза больше. Это связано с тем, что при вытекании жидкости в сосуде происходит перераспределение давления. должна быть равна силе гидростатического давления F2 = ghS (см. лекция 10, раздел 10.5), но реальная сила в 2 - раза больше. Это связано с тем, что при вытекании жидкости в сосуде происходит перераспределение давления.
б). На реакции вытекающей струи газа с двигающимся сосудом основано действие реактивного двигателя.
11.2. Ламинарное течение жидкостей.
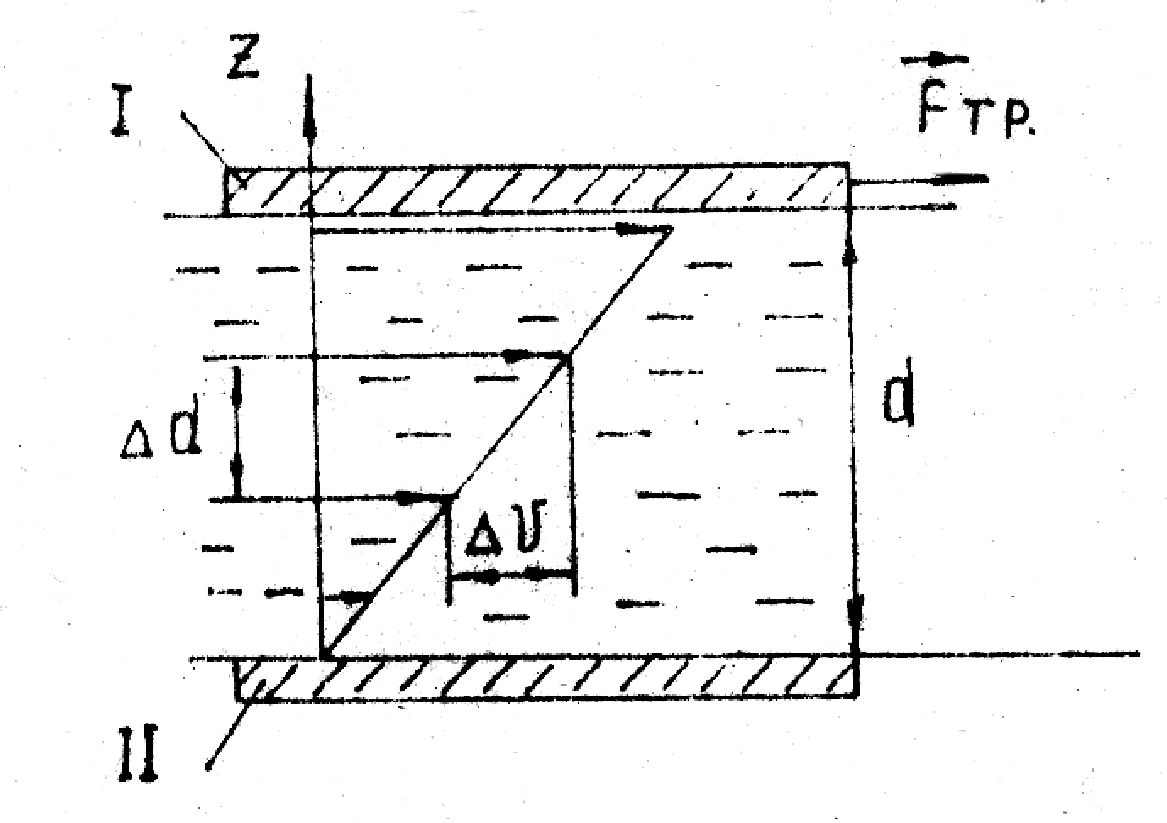
Течение жидкостей при наличии в них внутреннего трения, но не сопровождающееся образованием вихрей, называется ламинарным. Внутреннее трение возникает в жидкости вследствие взаимодействия её молекул. В отличие от внешнего трения, возникающего в месте соприкосновения двух тел, внутреннее трение имеет место внутри движущейся среды между слоями жидкости, движущимися с различными скоростями. Внутреннее трение проявляется при движении в жидкости пластинки параллельно плоской стенке. Для такого перемещения необходимо приложить силу, равную по величине Fтрения, причём экспериментально получено, что 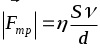 , где - динамическая вязкость (коэффициент внутреннего трения), S - площадь соприкосновения, d - расстояние между граничными плоскостями I и II. Полученное выражение справедливо и для промежуточных слоёв, находящихся друг от друга на расстоянии d< d, если в полученное выражение подставить значение относительной скорости, т.е. . , где - динамическая вязкость (коэффициент внутреннего трения), S - площадь соприкосновения, d - расстояние между граничными плоскостями I и II. Полученное выражение справедливо и для промежуточных слоёв, находящихся друг от друга на расстоянии d< d, если в полученное выражение подставить значение относительной скорости, т.е. .
Тогда 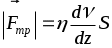 . .
Здесь d= z и dz, 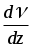 - величина градиент скорости. - величина градиент скорости.
Анализ:
1). Динамическая вязкость зависит от температуры 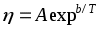 , где A и b- эмпирические постоянные, т.е. с повышением температуры вязкость жидкости уменьшается. У газов с повышением температуры вязкость увеличивается. , где A и b- эмпирические постоянные, т.е. с повышением температуры вязкость жидкости уменьшается. У газов с повышением температуры вязкость увеличивается.
2). [ ] = [ Па с ] или ранее [ П - пуаз.] 1П = 0,1 Па с = 0,1 нс/м2.
3). Кроме понятия динамическая вязкость применяются понятия: кинематическая вязкость и текучесть.
Текучесть ( ) - это величина обратная динамической вязкости, т.е. = 1 / , причём [ ] = [1/ Па с ].
Кинематической вязкостью () называется отношение динамической вязкости () к плотности среды ( ) или 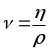 . Для кинематической вязкости [] = [ м2 / c ] или ранее [ Ст-стокс]. 1 Cт = 10 - 4 м2/c. . Для кинематической вязкости [] = [ м2 / c ] или ранее [ Ст-стокс]. 1 Cт = 10 - 4 м2/c.
4). Значение для отдельных жидкостей и газов:
Жидкость (при200С)
|
, м Па с
|
Газы (при200Си101кПа)
|
, м Па с
|
Ацетон
|
0,322
|
Азот
|
0,0175
|
Вода
|
1,002
|
Воздух
|
0,0182
|
Глицерин
|
1480
|
Кислород
|
0,0202
|
Cмола
|
3 . 1010
|
Метан
|
0,0108
|
При ламинарном течении жидкости по трубе отдельные её слои имеют разные скорости.
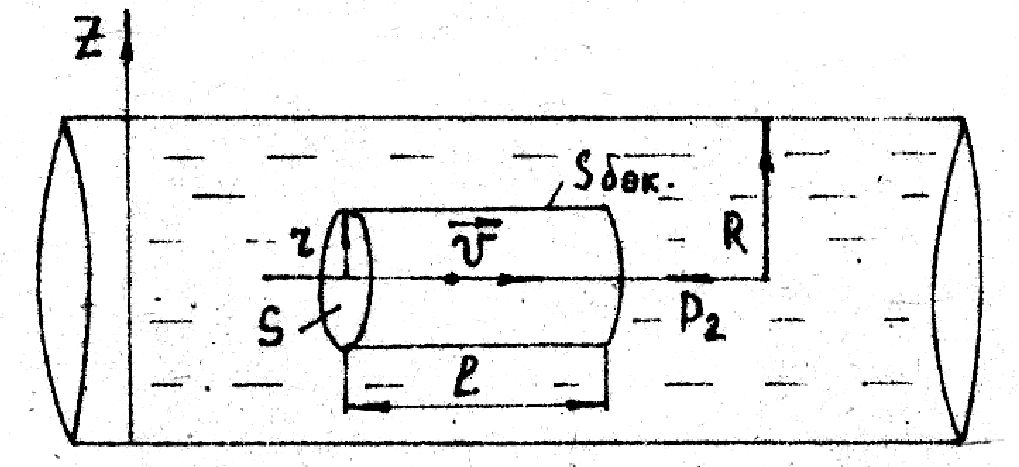
Дано: ламинарное течение жидкости по трубе.
Найти: закон изменения скорости по сечению трубы, (r).
Выделим в жидкости объём V, радиуса (r) и длиной (l). В направлении перемещения жидкости (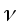 ) действует ) действует
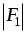 = p1S= p1r2, а в обратном направлении = p1S= p1r2, а в обратном направлении 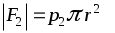 . . 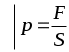
Следовательно  F1 - F2 = (p1 -p2)r2. На боковую поверхность (Sбок) объёма действует F1 - F2 = (p1 -p2)r2. На боковую поверхность (Sбок) объёма действует 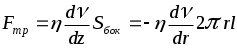 , где Sбок = 2rl . Знак минус указывает направление , где Sбок = 2rl . Знак минус указывает направление 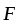 относительно относительно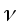 . Тогда в установившемся режиме течения жидкости: . Тогда в установившемся режиме течения жидкости:
(p1 - p2)r2 = 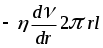 . .
Разделим переменные 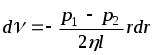 и проинтегрируем и проинтегрируем
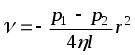 + Const. При r Rэкспериментально найдено, что + Const. При r Rэкспериментально найдено, что 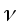 = 0, т.е. у стенки трубы = 0, т.е. у стенки трубы 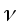 =0. Тогда Const = =0. Тогда Const = 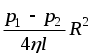 . Окончательно получим . Окончательно получим
 . .
Анализ:
а). Скорость по сечению трубы изменяется по параболическому закону, т.е.

б). (ось) - это скорость жидкости на оси трубы, которая равна
(ось) = 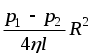 . .
V = S l
l = t
(r) = (ось) 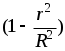
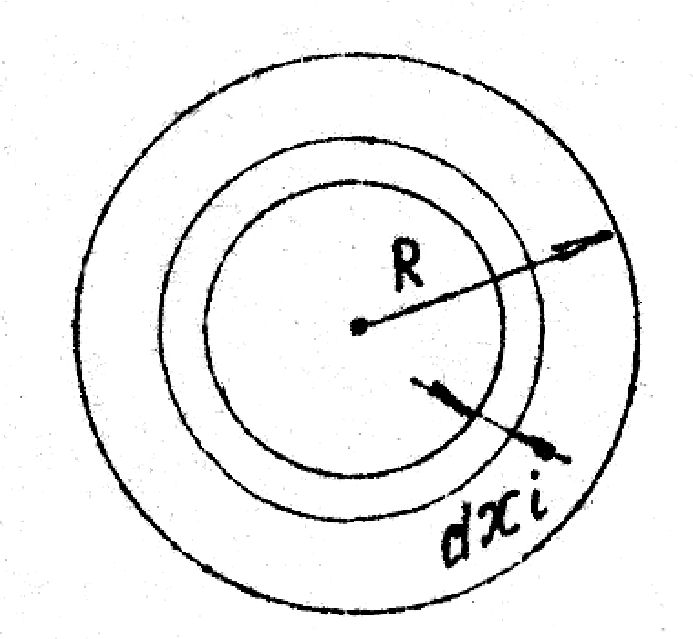
Разобьём сечение трубы на кольца шириной dr, причём площадь кольца
dS= 2ridri. Через эту площадь пройдёт объём жидкости
dV = 2ridri(r)t.
После подстановки
dV= (ось) 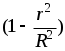 2rit dri и интегрирования 2rit dri и интегрирования
(ось) = 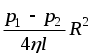
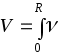 (ось) (ось) 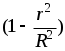 2ritdri= (ось) t 2ritdri= (ось) t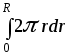 (ось) t (ось) t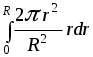 = =
(ось) t2 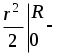 (ось) t (ось) t 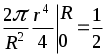 (ось) R2t. (ось) R2t.
Подставив (ось) получим
V= 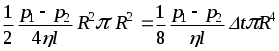 . .
Анализ:
а). Объём жидкости, протекающий по трубе, пропорционален перепаду давлений на единицу длины 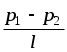 , радиусу трубы в 4-ой степени, времени, и обратно пропорционален вязкости ( ) жидкости. , радиусу трубы в 4-ой степени, времени, и обратно пропорционален вязкости ( ) жидкости.
б). Полученное выражение есть формула Пуазейля.
в). Эффективнее увеличить объём через радиус трубы, а не за счёт разности давлений (это используется в газопроводах).
г). Падение давления вдоль трубы с постоянным сечением пропорционально длине трубы, т.е. p l .
11.3. Турбулентное течение жидкости или газа.
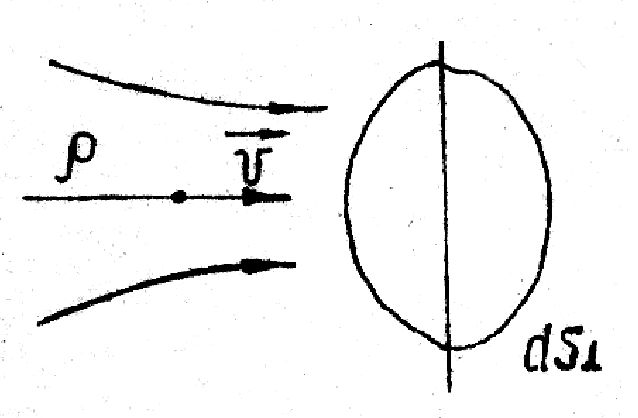
Течение жидкости при котором в каждой точке пространства направление скорости (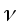 ) беспорядочно изменяется, называется турбулентным. При таком движении в жидкости возникают вихри, а следовательно, и силы, препятствующие течению. Сопротивление потоку, т.е. сила, действующая на помещённое в поток тело, складывается из разности p1 - p2 , где p1- давление перед, а p2 - давление после тела, а также силы трения (Fтр) на поверхности тела. Для тела произвольной формы сила гидравлического сопротивления (F): ) беспорядочно изменяется, называется турбулентным. При таком движении в жидкости возникают вихри, а следовательно, и силы, препятствующие течению. Сопротивление потоку, т.е. сила, действующая на помещённое в поток тело, складывается из разности p1 - p2 , где p1- давление перед, а p2 - давление после тела, а также силы трения (Fтр) на поверхности тела. Для тела произвольной формы сила гидравлического сопротивления (F):
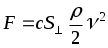 , ,
где с - коэффициент, зависящий от формы тела, S - площадь наибольшего сечения тела в плоскости, перпендикулярной направлению потока, - плотность жидкости (газа), - относительная скорость движения тела в среде.
Анализ:
1). Коэффициент с - безразмерное число. Определяется экспериментально и зависит от скорости.
 
        
   c= 1,11 c = 0,1 - 0,4 c= 1,11 c = 0,1 - 0,4
 тонкая пластина шар тонкая пластина шар
2). F зависит от 2, причём неважно что движется поток или само тело.
3). Коэффициент (с) зависит и от свойств среды, т.е. является функцией числа Рейнольдса (Re): 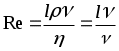 . Здесь l - характерные размеры тела (радиус шара, диаметр трубы и т.д.) - плотность и динамическая вязкость среды, - скорость тела относительно среды, - кинематическая вязкость. . Здесь l - характерные размеры тела (радиус шара, диаметр трубы и т.д.) - плотность и динамическая вязкость среды, - скорость тела относительно среды, - кинематическая вязкость.
Для малых Re (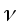 - мало) течение жидкости - ламинарное. При возрастании - мало) течение жидкости - ламинарное. При возрастании 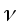 и достижения = крит, то ламинарное движение переходит в турбулентное и гидравлическое сопротивление резко возрастает.Reкрит = 1000 для потока в гладких трубах, однако это значение сильно зависит от состояния ее поверхности и условий течения жидкости (газа) и может достигать 2 104 . и достижения = крит, то ламинарное движение переходит в турбулентное и гидравлическое сопротивление резко возрастает.Reкрит = 1000 для потока в гладких трубах, однако это значение сильно зависит от состояния ее поверхности и условий течения жидкости (газа) и может достигать 2 104 .
Число Рейнольдса не изменяется при одновременном уменьшении размеров тела и , соответственно, увеличении потока или уменьшении .
Закон подобия: коэффициенты (с)геометрически подобных тел равны, если равны соответствующие числа Рейнольдса. В этом случае оба потока подобны.
11.4. Движение тел в жидкостях и газах.
Закон подобия позволяет проводить исследования сложных процессов, используя модели обтекаемых тел.
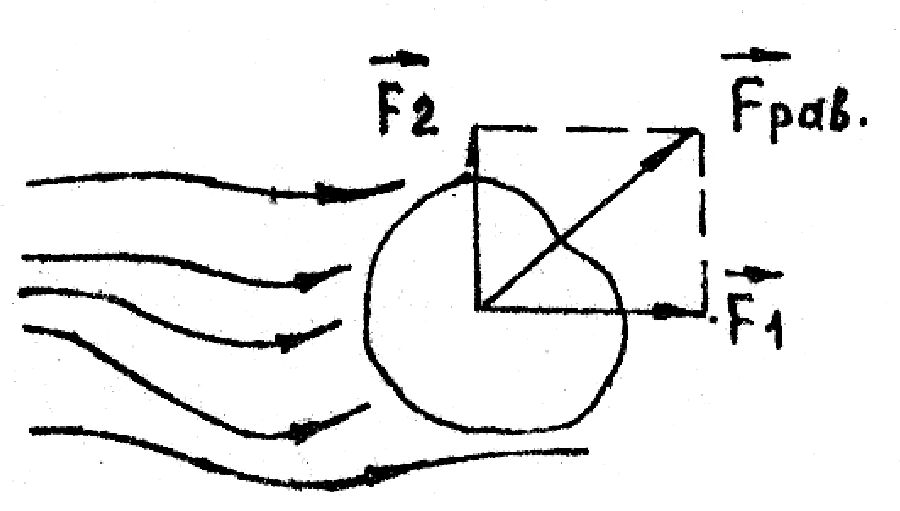
При движении тела в жидкости на него действуют силы, равнодействующую которых 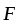 рав можно разложить на две составляющих: рав можно разложить на две составляющих: 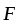 1 - сила лобового сопротивления, 1 - сила лобового сопротивления, 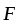 2 - подъёмная сила. 2 - подъёмная сила.
Если тело обтекаемой формы (симметричное относительно направления движения жидкости), то 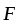 2= 0 и 2= 0 и 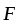 рез совпадает с рез совпадает с 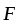 1. 1.
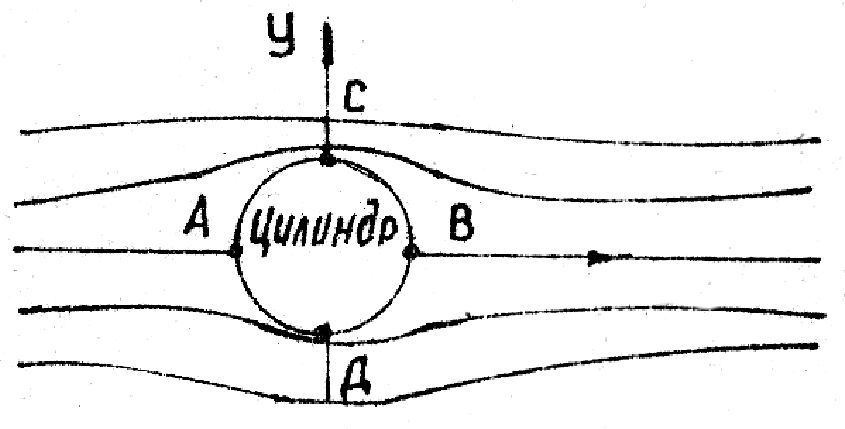
В идеальной жидкости при 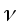 = Const, = Const, 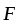 1 = 0 , т.е. лобового сопротивления нет. Так как вязкости нет, такая жидкость скользит по поверхности тела, обтекая его. Линии тока в данном случае симметричны относительно осей X и Y. Поэтому pA= pB и больше, чем в невозмущенном потоке, так как 1 = 0 , т.е. лобового сопротивления нет. Так как вязкости нет, такая жидкость скользит по поверхности тела, обтекая его. Линии тока в данном случае симметричны относительно осей X и Y. Поэтому pA= pB и больше, чем в невозмущенном потоке, так как 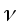 в этих точках меньше. Давление pC= pD и меньше, чем в невозмущённом потоке, т.к. в этих точках меньше. Давление pC= pD и меньше, чем в невозмущённом потоке, т.к. 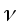 вблизи этих точек больше. Следовательно вблизи этих точек больше. Следовательно 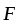 рез = 0. рез = 0.
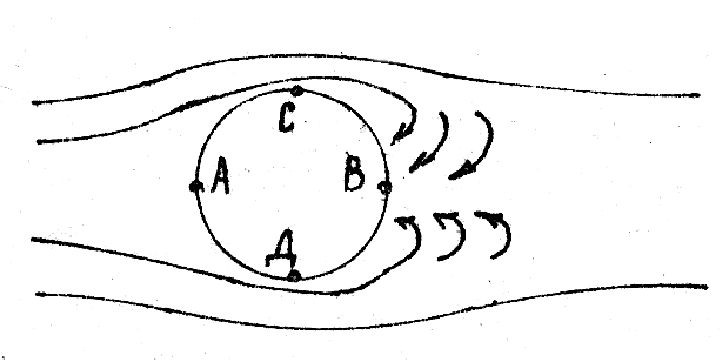
При движении тела в жидкости с вязкостью тонкий её слой "прилипает" к поверхности тела и движется с ним как единое целое. Кроме того, такой слой из-за трения увлекает за собой и другие соседние слои. Таким образом, тело оказывается окружённым слоем жидкости, конечной длины (вдали от тела его влияние не проявляется), в котором существует 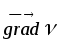 . Этот слой называется пограничным. . Этот слой называется пограничным.
Такое поведение вязкой жидкости приводит к:
а. Изменению характера движения жидкости. Полного обтекания нет.
б. Позади тела из-за отрыва потока от тела возникают вихри, которые уносятся потоком и затухают. Энергия вихрей расходуется на нагрев жидкости. Затухания вихрей происходит из-за трения в жидкости.
в. Давление pB < pA, поэтому возникает 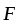 рез 0, обуславливая рез 0, обуславливая 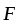 1 - лобовое сопротивление. 1 - лобовое сопротивление.
г. Fрез - состоит из F1 и F2 .
д. Соотношение между F1 и F2 определяется числом Рейнольдса (Re).
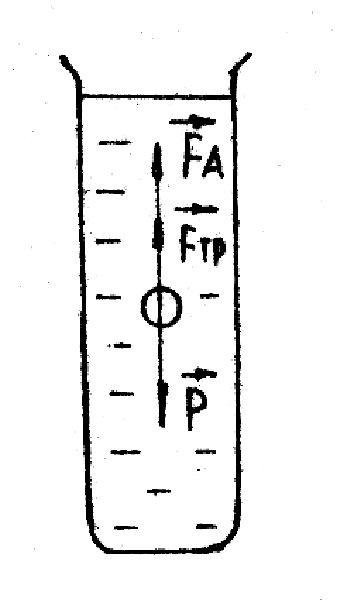
При малых Re, т.е. при 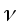 - мало, сопротивление среды обусловлено только действием силы трения. Сила сопротивления движению тела (шара) в такой среде - мало, сопротивление среды обусловлено только действием силы трения. Сила сопротивления движению тела (шара) в такой среде
Fсопр = Fтр = 6r,
где - коэффициент динамической вязкости, r - радиус шара, - скорость шара относительно жидкости.
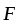 A= A=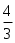 r3жg r3жg
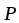 = mg= = mg=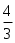 r3шg r3шg
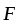 тр= 6 r тр= 6 r
На движущийся в жидкости шар действуют 3 силы: 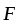 A - архимедова сила, A - архимедова сила, 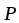 - сила тяжести (вес) и - сила тяжести (вес) и 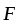 тр - сила трения. тр - сила трения.
При равномерном движении
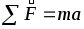 ; ; 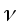 = Const = 0 . = Const = 0 . 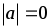 и и
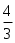 r3ш g = r3ш g = 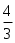 r3ж g + 6r0 . r3ж g + 6r0 .
Отсюда 0 = 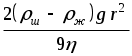 . .
Анализ:
1). 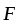 тр = 6r- называется силой Стокса. тр = 6r- называется силой Стокса.
2). Формула для 0 справедлива для малых по диаметру шаров.
3). На законе Стокса основано определение вязкости жидкости вискозиметром Гёпплера. |
 Скачать 1.18 Mb.
Скачать 1.18 Mb.
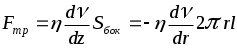 , где Sбок = 2rl . Знак минус указывает направление
, где Sбок = 2rl . Знак минус указывает направление 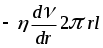 .
.

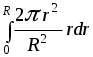 =
= 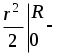 (ось) t
(ось) t 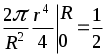 (ось) R2t.
(ось) R2t.
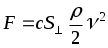 ,
,












 c= 1,11 c = 0,1 - 0,4
c= 1,11 c = 0,1 - 0,4 тонкая пластина шар
тонкая пластина шар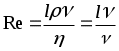 . Здесь l - характерные размеры тела (радиус шара, диаметр трубы и т.д.) - плотность и динамическая вязкость среды, - скорость тела относительно среды, - кинематическая вязкость.
. Здесь l - характерные размеры тела (радиус шара, диаметр трубы и т.д.) - плотность и динамическая вязкость среды, - скорость тела относительно среды, - кинематическая вязкость.









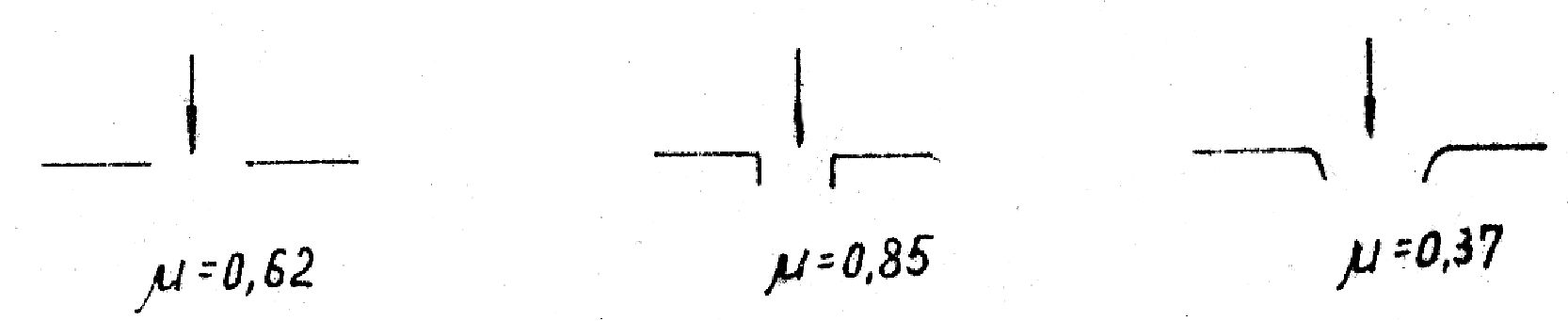


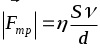 , где - динамическая вязкость (коэффициент внутреннего трения), S - площадь соприкосновения, d - расстояние между граничными плоскостями I и II. Полученное выражение справедливо и для промежуточных слоёв, находящихся друг от друга на расстоянии d< d, если в полученное выражение подставить значение относительной скорости, т.е. .
, где - динамическая вязкость (коэффициент внутреннего трения), S - площадь соприкосновения, d - расстояние между граничными плоскостями I и II. Полученное выражение справедливо и для промежуточных слоёв, находящихся друг от друга на расстоянии d< d, если в полученное выражение подставить значение относительной скорости, т.е. . 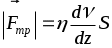 .
.