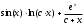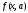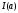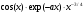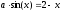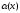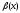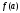Лабораторная ООП. Задача Вычисление определенного интеграла Написать программу для вычисления определенного интеграла как функции параметра с
 Скачать 76.05 Kb.
|
|
Задача 1. Вычисление суммы ряда Написать программу для вычисления суммы ряда S при заданном значении параметра a. Точность получаемого результата проверить, а) изменяя порядок суммирования; б) увеличивая количество суммируемых членов ряда. Описание суммируемых рядов и величина суммы при некоторых значениях параметра 
Задача 2. Вычисление определенного интеграла Написать программу для вычисления определенного интеграла 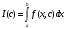 как функции параметра с.Точность получаемого результата проверить, а) увеличивая в несколько раз число отрезков, на которые делится отрезок [a,b]; б) сопоставляя численный и аналитический результат для тестового варианта расчета – интегрирования полинома – и принимая во внимание, что с помощью формул прямоугольников и трапеций точно интегрируется линейная функция, а с помощью формулы Симпсона – произвольный полином третьей степени Подынтегральные функции, пределы интегрирования и величина интеграла при некоторых значениях параметра 
Задача 3. Вычисление несобственного интеграла Написать программу для вычисления несобственного интеграла вида 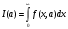 как функции параметра a.Точность получаемого результата проверить, а) увеличивая в несколько раз число отрезков разбиения; б) сопоставляя численный и аналитический результат для тестового варианта расчета – интегрирования полинома – и принимая во внимание, что с помощью формул прямоугольников и трапеций точно интегрируется линейная функция, а с помощью формулы Симпсона – произвольный полином третьей степени [1]; в) изменяя размер окрестности точки x = 0, в которой производится аналитическое интегрирование приближенной подынтегральной функции. Подынтегральные функции, пределы интегрирования и величина интеграла при некоторых значениях параметра
Задача 4. Решение трансцендентного уравнения Найти корень уравнения в указанном диапазоне значений x(считать, что a>0). Уравнение, область поиска решения и величина корня при некоторых значениях параметра
Задача 5. Поиск минимального и максимального элементов одномерного массива Найти номера Nmin и Nmaxминимального и максимального элементов одномерного массива F(N) в диапазоне 1 N 100000: 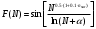 ,здесь > 0 – численный параметр, nvar – номер варианта. Номера Nmin и Nmaxминимального и максимального элементов одномерного массива (верхняя строка в каждой ячейке таблицы соответствует значению параметра 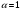 , нижняя строка – значению  )
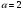Задача 6. Определение минимального собственного значения эрмитовой матрицы Найти минимальное собственное значение Emin() квадратной симметричной действительной матрицы F(N,M); 1 M,N 100 при заданном значении параметра > 0: 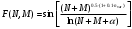 , где nvar – номер варианта.Значение минимального собственного значения Emin эрмитовой матрицы. (верхняя и нижняя строки в каждой ячейке таблицы соответствуют значениям параметра 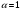и 2 соответственно)
Задача 7. Упорядочение элементов одномерного массива Даны элементы одномерного массива F(N) с N = 100000, определяемые генератором случайных чисел и распределенные хаотически в интервале от нуля до единицы. Требуется упорядочить этот массив в порядке возрастания его элементов: F(1) <F(2) < ... <F(N). При сдаче этого задания необходимо уметь находить величину F(No) по заданному номеру элемента No. На языке FORTRAN подпрограмма-функция ran(iy) для генерации случайных чисел имеет следующий вид: function ran (iy) REAL*8RAN data mo,mn,mdb/65536,25137,13849/,ab/65536/ iy=mod(mn*iy+mdb,mo) ran=iy/ab return end В этой программе оператор mod(I, J) определяет остаток от деления числа I на число J. Первоначальное значение параметра iy полагать равным 1000·nvar+1, где nvar – номер варианта. После определения первого случайного числа параметр iy в процессе счета изменяется только подпрограммой ran (iy).
Задача 8. Решение обыкновенного дифференциального уравнения На интервале [0, 2] найти решение дифференциального уравнения 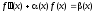 , периодическое с периодом 2. Построить график функции f(x) на интервале [0, 2], используя стандартное программное обеспечение. Определить значение f(a) при произвольной величине a[0, 2] путем интерполяции.Переменные коэффициенты дифференциального уравнения и значение 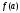 при a = 1 и 2 (верхняя и нижняя строки ячейки, соответственно)
Задача 9. Определение корней кубического уравнения Найти корни кубического уравнения x3 + ax2 + bx + c = 0 с комплексными коэффициентами. После нахождения корней уравнения необходимо выполнить проверку каждого из них путем подстановки в исходное уравнение.
|
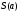
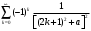
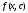
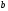
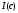при данном 
