биофизика. Биофизика_1504-152. Задача задача 15
 Скачать 41.06 Kb. Скачать 41.06 Kb.
|
|
СОДЕРЖАНИЕ
Задача 5. С каким грузом человек массой 80 кг приподнимется на полупальцы, если мышечное усилие одной ноги составляет 1500 Н, расстояние от точки опоры до линии действия силы тяжести 0,18 м, а расстояние от точки опоры до точки крепления ахиллова сухожилия 0,22 м? Решение: В данном случае, исходя из биомеханических процессов, происходящих в теле человека, имеет место так называемый рычаг второго рода, схема действия которого показана на рисунке 1. 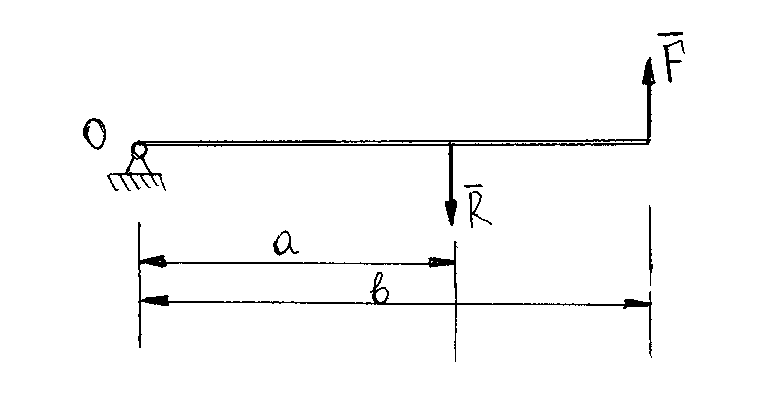 Рисунок 1. На этом рисунке ось вращения O проходит через точку опоры и на стопу человека действуют две силы, приложенные по одну сторону оси: - сила тяжести R, равная половине силы тяжести, действующей на все тело человека; - сила тяги мышц F, передаваемая с помощью ахилловых сухожилий и приложенная к выступу пяточной кости. Плечи действия вышеописанных сил следующие: - для силы тяжести это  – расстояние от точки опоры до линии действия силы тяжести; – расстояние от точки опоры до линии действия силы тяжести;- для мышечного усилия это  – расстояние от точки опоры до точки крепления ахиллова сухожилия. – расстояние от точки опоры до точки крепления ахиллова сухожилия.В нашем случае, согласно данным условия задачи, эти величины равны:  , ,  . .Условие равновесия рычага можно представить в виде: 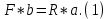 Расчет будем вести для двух ног сразу. В этом случае мышечное усилие 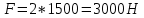 , сила тяжести , сила тяжести 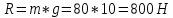 . .Здесь  – заданная масса человека; – заданная масса человека;  – ускорение свободного падения, значение которого принято округленно для упрощения расчетов (расхождение с действительным значением 9,81 не так уж велико и составляет 1,9%). – ускорение свободного падения, значение которого принято округленно для упрощения расчетов (расхождение с действительным значением 9,81 не так уж велико и составляет 1,9%).При решении задачи необходимо определить вес груза 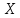 , с которым человек сможет приподняться на полупальцы. Поэтому окончательно на основании уравнения равновесия (1), можем записать: , с которым человек сможет приподняться на полупальцы. Поэтому окончательно на основании уравнения равновесия (1), можем записать: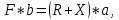 откуда выражаем: 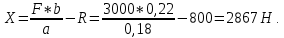 Значит, соответствующая масса искомого груза: 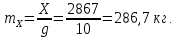 Задача 15. Минутный дыхательный объем человека  , температура вдыхаемого воздуха , температура вдыхаемого воздуха  , относительная влажность 60%, а температура выдыхаемого воздуха , относительная влажность 60%, а температура выдыхаемого воздуха  . Определить количество воды, испаряющейся через легкие в течение суток, если выдыхаемый из легких воздух полностью насыщен водяными парами, а плотность насыщенного пара при . Определить количество воды, испаряющейся через легкие в течение суток, если выдыхаемый из легких воздух полностью насыщен водяными парами, а плотность насыщенного пара при  равна равна  ; при ; при  составляет составляет  . .Решение: Обозначим через 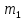 – массу воды, попадающей в легкие при вдохе; через – массу воды, попадающей в легкие при вдохе; через 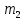 – массу воды, выходящей из легких с выдыхаемым воздухом. – массу воды, выходящей из легких с выдыхаемым воздухом.Известна взаимосвязь между массой 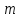 , плотностью , плотностью  и объемом и объемом  : :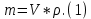 Тогда, учитывая, что во вдыхаемом воздухе только 60% насыщенных водяных паров получаем: 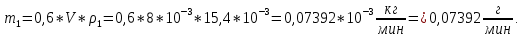 Соответственно, для выдыхаемого воздуха, полностью насыщенного водяными парами, получаем:  Определяем искомое количество воды, испаряющееся через легки в течение суток:  Задача 25. При диатермии печени крупного рогатого скота один электрод размером  накладывают спереди на область печени, а второй – сзади напротив первого. Сила тока между электродами I=1,1 А. Процедуру проводят t=15 минут=15*60=900 c. Какое количество теплоты выделится в заключенном объеме печени толщиной d=5 см? Удельное сопротивление печени накладывают спереди на область печени, а второй – сзади напротив первого. Сила тока между электродами I=1,1 А. Процедуру проводят t=15 минут=15*60=900 c. Какое количество теплоты выделится в заключенном объеме печени толщиной d=5 см? Удельное сопротивление печени  . .Решение: Прежде всего, по заданным параметрам рассчитываем заключенный объем печени:  Искомое количество теплоты, выделяющееся при диатермии, определится по следующей формуле: 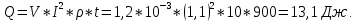 Задача 35. При прохождении света через раствор крови в кювете высотой 5 см интенсивность света уменьшилась на 8%. Определите концентрацию раствора, если известно, что для него удельный показатель поглощения равен  . .Решение: В соответствии с законом Бугера интенсивность света, прошедшего через слой вещества толщиной  , уменьшается по экспоненциальному закону: , уменьшается по экспоненциальному закону: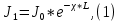 где  – показатель поглощения вещества. – показатель поглощения вещества.Из формулы (1) получаем:  Логарифмируем выражение (2):  откуда показатель поглощения вещества равен: 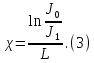 Поглощение монохроматического света окрашенными растворами подчиняется закону Бера, согласно которому показатель поглощения пропорционален концентрации вещества в растворе: 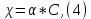 где 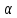 – удельный показатель поглощения. – удельный показатель поглощения.Сопоставляя соотношениям (3) и (4), получим выражение искомой концентрации раствора:  По условию задачи известно:  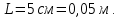 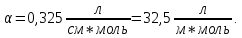 Производим вычисления по формуле (5):  ЛИТЕРАТУРА 1. Белановский А.С. Основы биофизики в ветеринарии: учебное пособие для вузов / А.С. Белановский.– 4-е изд., перераб. и доп.– М.: Дрофа, 2007.– 332 с. 2. Грабовский Р.И. Курс физики: учебное пособие для высших сельскохозяйственных ВУЗов / Р.И. Грабовский.– 6-е изд., перераб. и доп.– М.: Высшая школа, 2004.– 605 с. 3. Даниленко Л.П. Физика и биофизика: учебно-методическое пособие для ВУЗов / В.И. Соболевский, Л.П. Даниленко, О.В. Пышненко; под ред. В.И. Соболевского.– Витебск: ВГАВМ, 2008.– 132 с. |
