шпоры практика моделирование-1. Задача закрытого типа Транспортная задача открытого типа
 Скачать 453.73 Kb.
|
|
1.Календарного планирования о 2 станках 2.Календарного планирования о 4 станках 3.Транспортная задача закрытого типа 4.Транспортная задача открытого типа 5.Распределительная задача 6.Задача планирования производственной программы предприятия 7.Оптимизация раскроя плитных материалов 8.Сетевого планирования 1.Календарного планирования о 2 станках Алгоритм Джонсона 1 группа: детали, у которых время обраб. на 1 станке не превышает времени обраб. на 2 станке 2 группа: детали, у которых время обраб. на 1 станке больше времени обраб. на 2 станке(все те ,что не подошли к 1 группе) Вначале обраб. детали 1 гр. в порядке возрастания длит-сти их обраб. на 1 станке. После этого запускают детали 2 гр., в порядке убывания их работы на 2 станке. После этого рисуется график Ганта Например:
1 гр: 1,3,5 2 гр: 2,4,6 Порядок запуска: 3,5,1,6,4,2 График Ганта 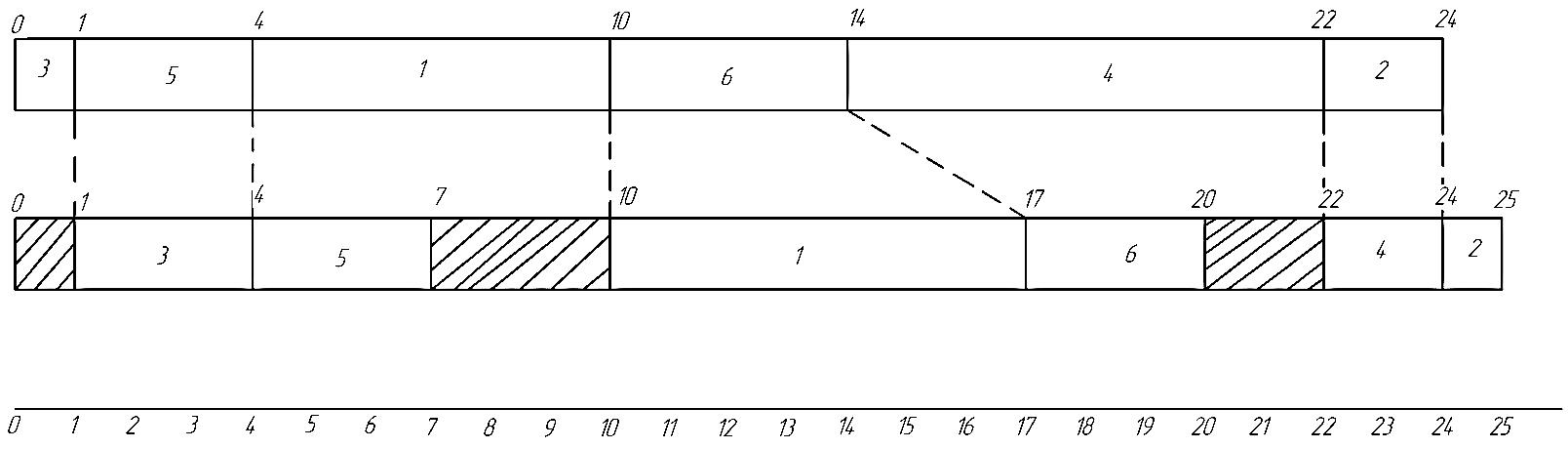 Сумарн. Время обраб всех деталей = 25, при этом 1 станок работает без простоев, а сумарн. Время простоя 2 станка=1+3+2=6 2.Календарного планирования о 4 станках Правила запуска деталей в обработку:” Детали запуск. в порядке…” 1. возрастания времени обраб. на 1 станке 2. убывания времени обраб. на последнем станке 3.убывания времени обраб. на станке, кот. явл. “Узким местом” “Узким местом” называется станок, суммарное время обработки на котором всех деталей max 4.в порядке убывания суммарного времени обраб. их на всех станках Например:
-рисуем графики Ганта - составляем таблицу (для всех последовательностей)
3.Транспортная задача закрытого типа 1.Заполняем таблицу, исходя из условия 2.Составляем опорный план перевозок N=m+n-1=кол-во заполненных клеток W= 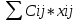 (по заполненным)3.Находим потенциалы( для этого один из потенциалов принимаем=0) Рассчитываем оценки δij=Cij-(Vij+Uij) Если есть все оценки положительные- задача решена(план оптимален) Если есть ‘-‘ ,план не оптимальный,необходимо перераспределение перевозок Для этого мы строим цикл Цикл строится из клетки с max по модулю отриц. знач. ( в этой клетке ставим +,дальше идем по заполненным клеткам, чередуя +/-, цикл это многоугольник ,у которого все углы прямые) Из значений в клетках цикла с ‘-‘ выбираем наименьшее число, его будем отнимать или добавлять(ТОЛЬКО НА УГЛАХ ЦИКЛА) Строим новую таблицу, учитывая изменения значений, Далее повторяем все действия с пункта 2 4.Транспортная задача открытого типа Решение т.з. открытого типа сводится к решению т.з закрытого типа , для этого: Вводим фиктивного поставщика*(сумма Ai < суммы Bj) или потребителя&(сумма Ai > суммы Bj) При этом стоимость перевозки у фиктивного */& будет =0 Далее решение аналогично решению т.з закрытого типа Методы решения Т.З. 1. наименьшей стоимости Заполнение таблицы происходит от меньшей стоимости к большей 2. северо-западного угла Заполнение таблицы начинается с клетки x11(верхний левый угол) И далее заполняется 1 строка, потом 2 ,3 и т.д 5.Распределительная задача Решение аналогично решению транспортной задачи закрытого типа , только вместо кол-ва груза будет либо ‘1’ либо ‘0’ 0 нужно добавлять так, чтобы не получился цикл. 6.Задача планирования производственной программы предприятия Пример
П1=10 у.е.П2=8 у.е. 1.целевая функция W=10*x1+8*x2→max 2. составим ограничения 2x1+4x2≤160 x1+3x2≤90 3x1+3x2≤150 x1≤40 (графический метод) Оси x1 и x2 3. неравества преобразовываем в уравнения 1)2x1+4x2=160 2) x1+3x2=90 3)3x1+3x2=150 4)x1=40 Для того чтобы решить уравнения ,одну из переменных принимаем=0,и ищем 2ую,т.о 1 точку с 2-мя координатами, затем 2ую перемен.=0,ищем значение 1-ой переменной- координата 2 точки 1)x1=0 x2=40 x2=0 x1=80 2)x1=0 x2=30 x2=0 x1=90 3)x1=0 x2=50 x2=0 x1=50 4)x1=40 4.Строим эти прямые на коорд. Плоскости 5.Заштрих. область допуск. решений 6.Строим вектор градиента( градиент- вектор,который начинается в начале координат проходит ч/з точку коорд. которой = стоимости соотв. прод. 7. Строим пряму. W=const, которая перпендикулярна вектору градиента(п.6) Далее перемещаем прямую W=const в направлении градиента целевой функции до тех пор, пока не останется только 1 общ. точка, принадлеж. области допускаемых решений- точка оптимума 8. Определить на пересечении каких прямых лежит т. оптимума т. лежит на пересеч. 3 и 4 прямой 3x1+3x2=150 x1=40 3x2=150-120 x2=10 W=10*40+8*10=480 График 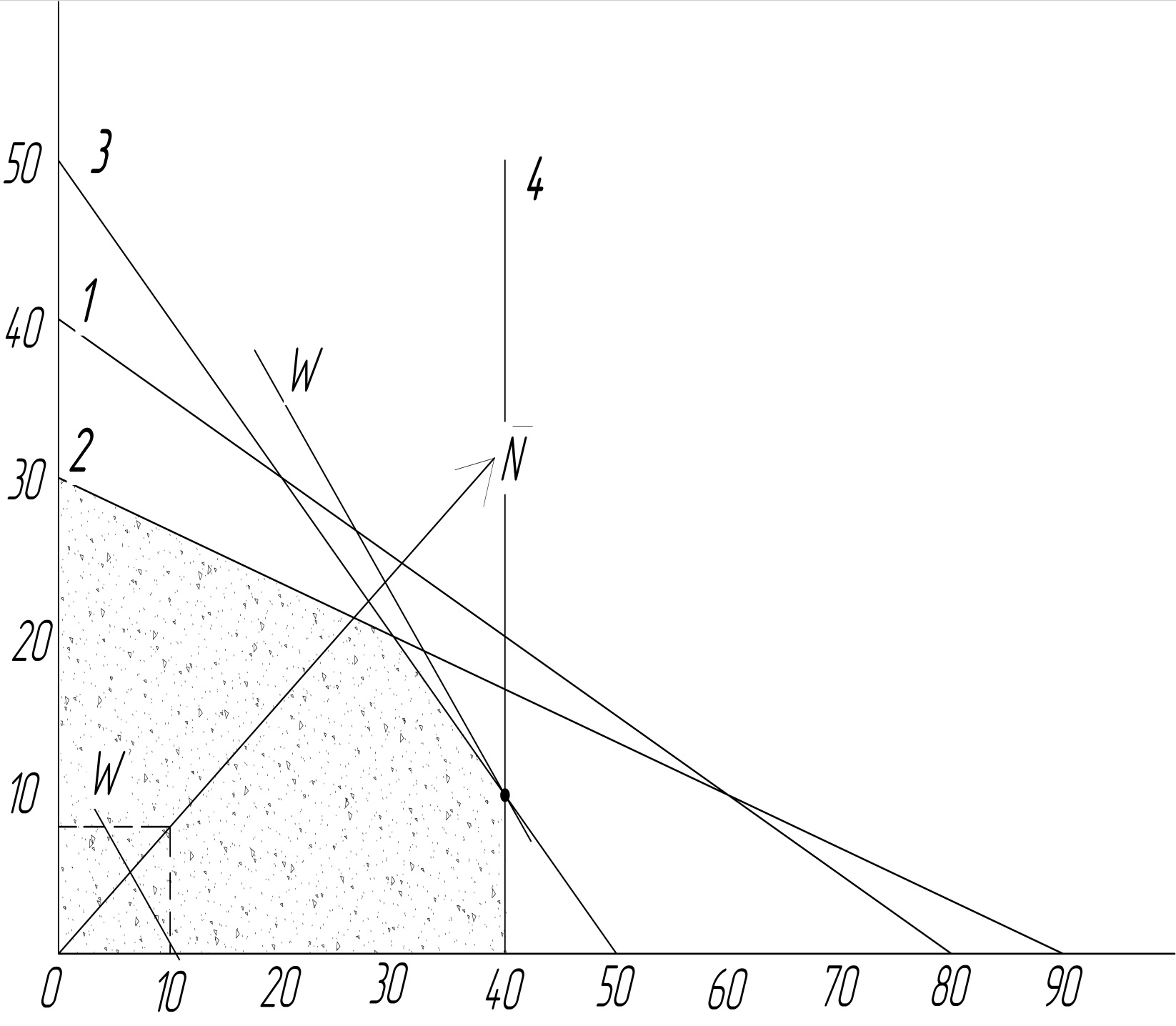 (Симплекс метод) 3. неравества преобразовываем в уравнения 1)2x1+4x2+x3=160 2) x1+3x2+x4=90 3)3x1+3x2+x5=150 4)x1+x6=40 Примечание: ≤ ‘-‘xn ≥ ‘+’xn х3,х4,х5,х6-доп.переменные
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
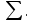вр.простоя