Задачи для контрольных заданий Элементы линейной алгебры и аналитической геометрии

• Название: Задачи для контрольных заданий Элементы линейной алгебры и аналитической геометрии
• Дата: 24.05.2021
• Размер: 371.5 Kb.
• Имя файла: 61Д.doc
• Тип: Документы; #209179

Задачи для контрольных заданий

1. Элементы линейной алгебры и аналитической геометрии

Вариант – 6
11-20. Даны координаты вершин пирамиды А₁А₂А₃А₄ .Найти:

1) длину ребра А₁А_2;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол меж­ду ребром А₁А₄и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объем пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

8) уравнение высоты, опущенной из вершины А₄на грань А₁А₂А₃. Сде­лать чертеж.



Решение:

Найдем координаты векторов по формуле:

X = x_j - x_i; Y = y_j - y_i; Z = z_j - z_i
здесь X,Y,Z координаты вектора; x_i, y_i, z_i - координаты точки А_i; x_j, y_j, z_j - координаты точки А_j;
A₁A₂(4;-6;4);
A₁A₃(4;-1;2);
A₁A₄(3;2;7).

1) длину ребра А₁А₂ найдем как расстояние между двумя точками и по формуле



A₁A₂(4;-6;4);
.

2) косинус угла между векторами А₁А₂ и А₁А₄ найдем как угол между ненулевыми векторами 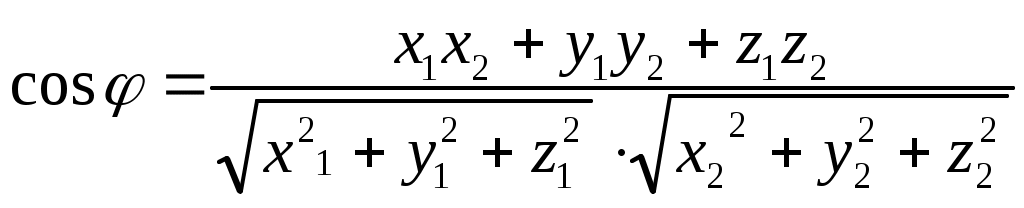и :

.

A₁A₂(4;-6;4); A₁A₄(3;2;7).

.
3) угол между ребром А₁А₄ и гранью А₁А₂А₃ найдем как угол между прямой и плоскостью Q: :

.
Найдем уравнение прямой А₁А₄:

А₁(1,8,2), А₄ (4,10,9).

; ;

Уравнение плоскости А₁А₂А₃ найдем как уравнение плоскости, проходящей через три точки 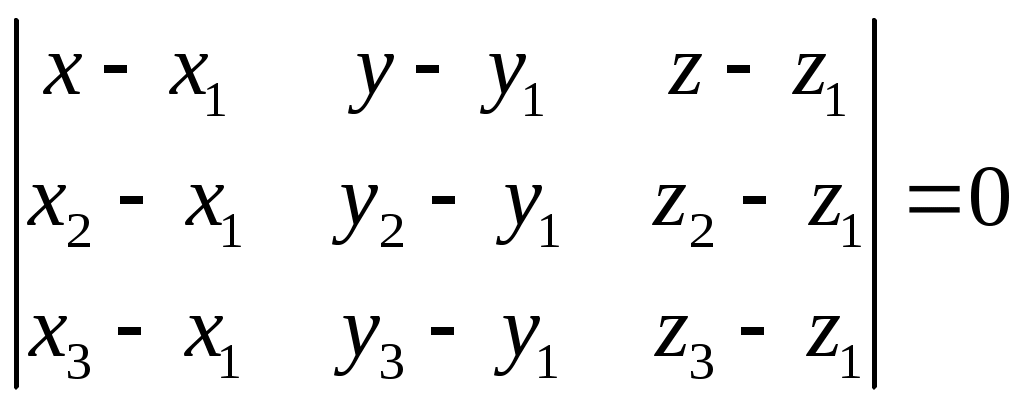, и :

.

А₁(1,8,2), А₂ (5,2,6) ,А₃ (5,7,3).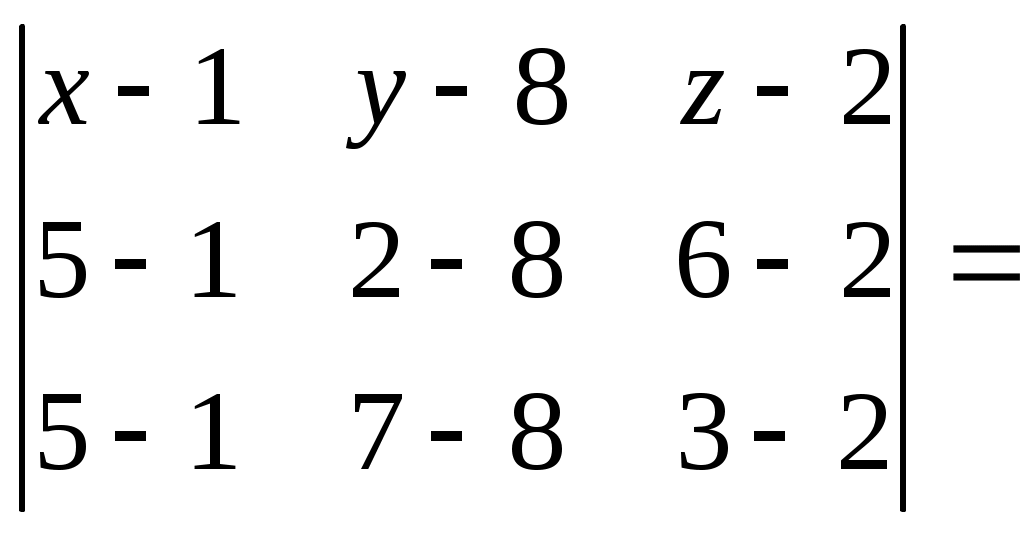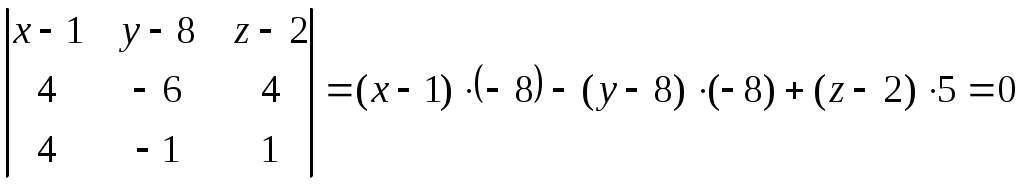



или .

.

= arcsin(0,73) = 46,89^o.

4) площадь грани А₁А₂А₃ найдем как площадь треугольника А₁А₂А₃ , построенного на векторах А₁А₂ и А₁А_3.

где - векторное произведение векторов.

Найдем координаты векторов:

A₁A₂(4;-6;4);
A₁A₃(4;-1;2);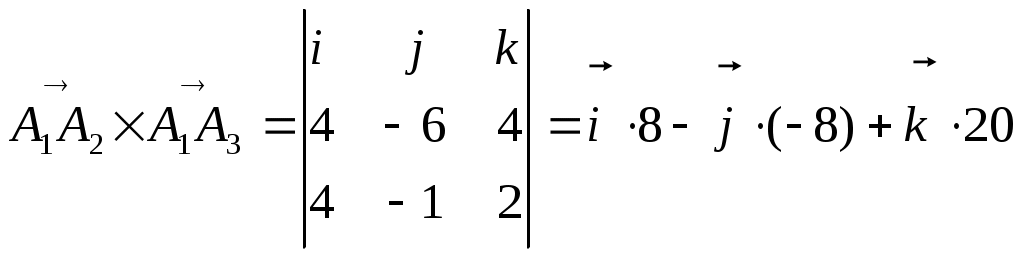
<sub>.

.</sub>


5) объём пирамиды, построенной на векторах вычисляется по формуле:

.

Найдем координаты векторов:

A₁A₂(4;-6;4);
A₁A₃(4;-1;2);
A₁A₄(3;2;7).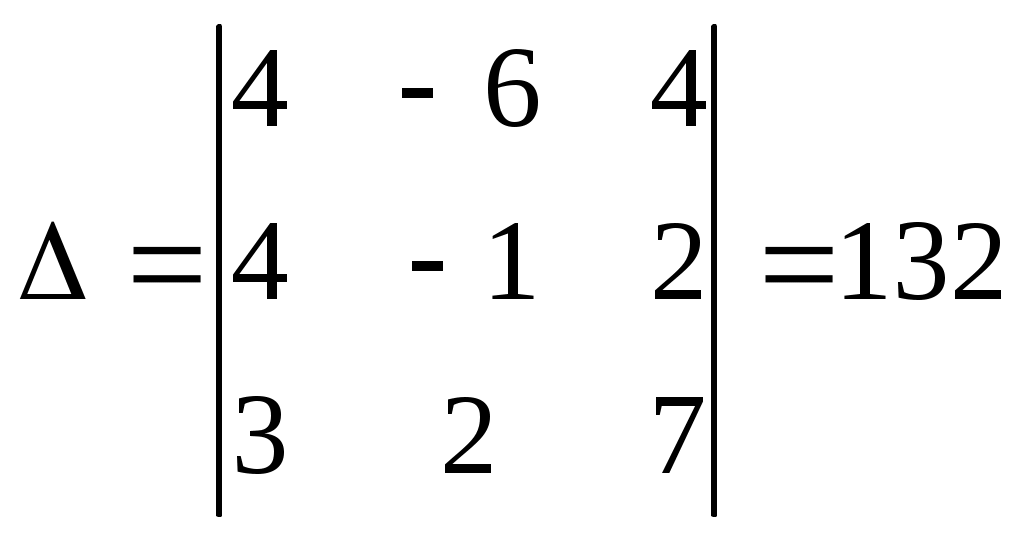
.

.
6) Уравнение плоскости А₁А₂А₃ найдем как уравнение плоскости, проходящей через три точки 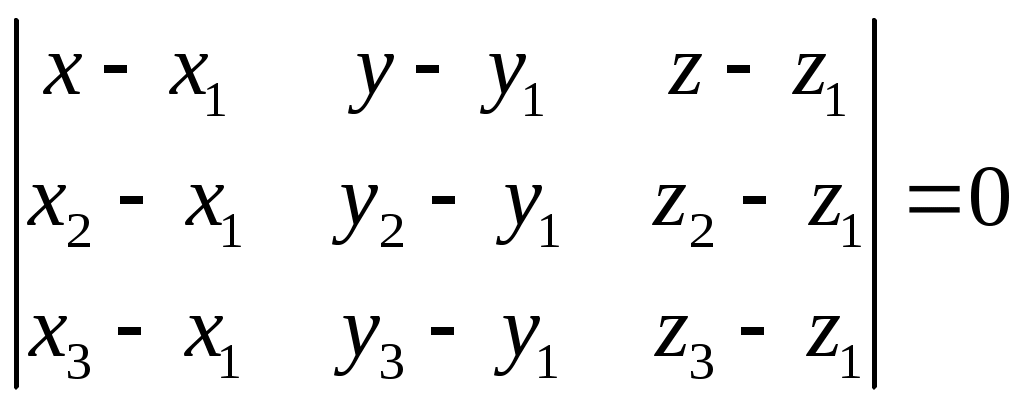, и :

.

А₁(1,8,2), А₂ (5,2,6) ,А₃ (5,7,3).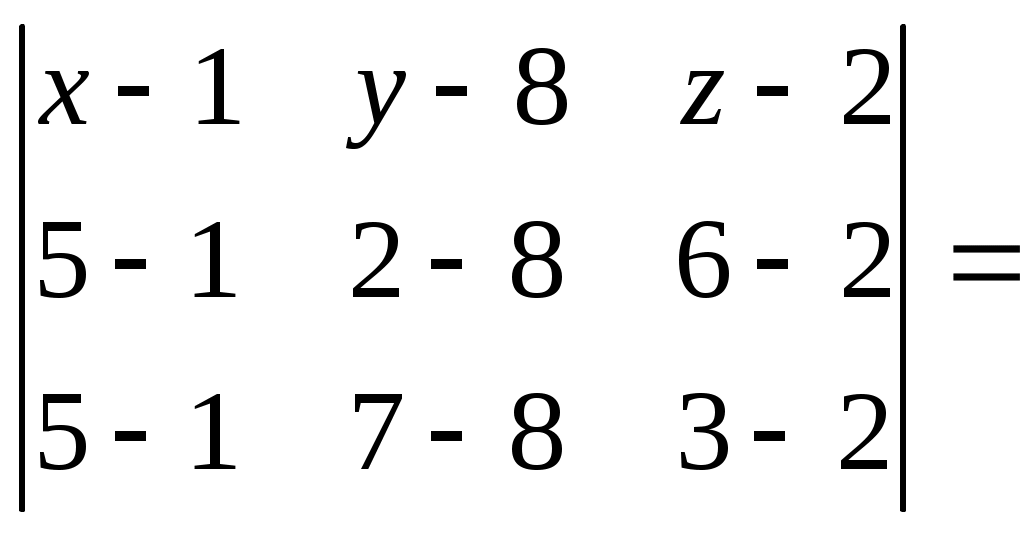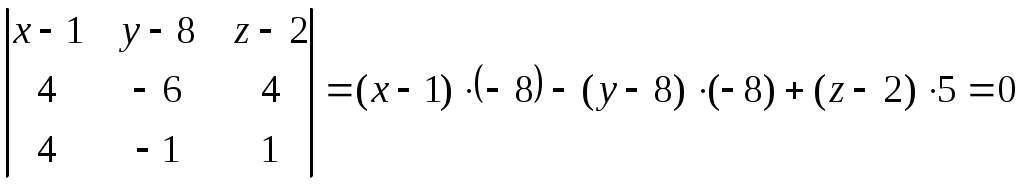



или .
7) уравнение прямой А₁А₂ найдем как уравнение прямой_, проходящей через две точки и :

.

А₁(1,8,2), А₂ (5,2,6)

; .
8) уравнение высоты, опущенной из вершины на грань ;
Уравнение высоты, опущенной из точки А₄ на грань А₁А₂А₃ найдем как каноническое уравнение прямой: , где - направляющий вектор прямой, - точка, лежащая на этой прямой.

Направляющим вектором искомой прямой будет нормальный вектор плоскости : , .

А₄ (4,10,9) - точка, лежащая на этой прямой.

Тогда уравнение высоты, опущенной из точки А₄ на грань А₁А₂А₃: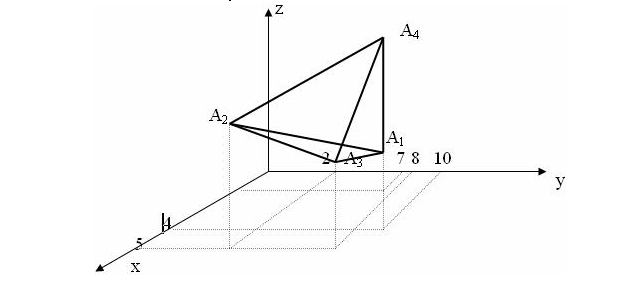

.


26. Даны уравнения двух сторон треугольника 5х - 4у + 15 = 0 и 4x+ у - 9 = 0. Его медианы пересекаются в точке (0,2). Составить уравнение третьей стороны треугольника.

Решение:

Найдем точку пересечения сторон:

.

.

А (1; 5).

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины треугольника.

Пусть АК – медиана.

Найдем координаты точки К:

; .

; .

А (1; 5) и К ( ; ).
Уравнение стороны ВС как уравнение прямой проходящей через точку К в заданном направлении: .

Найдем вершину В как точку пересечения прямой АВ и ВС:



Имеем абсциссу точки В:



Найдем вершину С как точку пересечения прямой АС и ВС:



Имеем абсциссу точки С:

.

Так как точка К – середина отрезка ВС:

.

.

.



Ответ: уравнение третьей стороны: .

Задания 41-50. Найти пределы функций, не пользуясь правилом Ло­питаля.

46.

а) .

Решение:

Непосредственная подстановка предельного значения аргумента приводит к неопределенному выражению 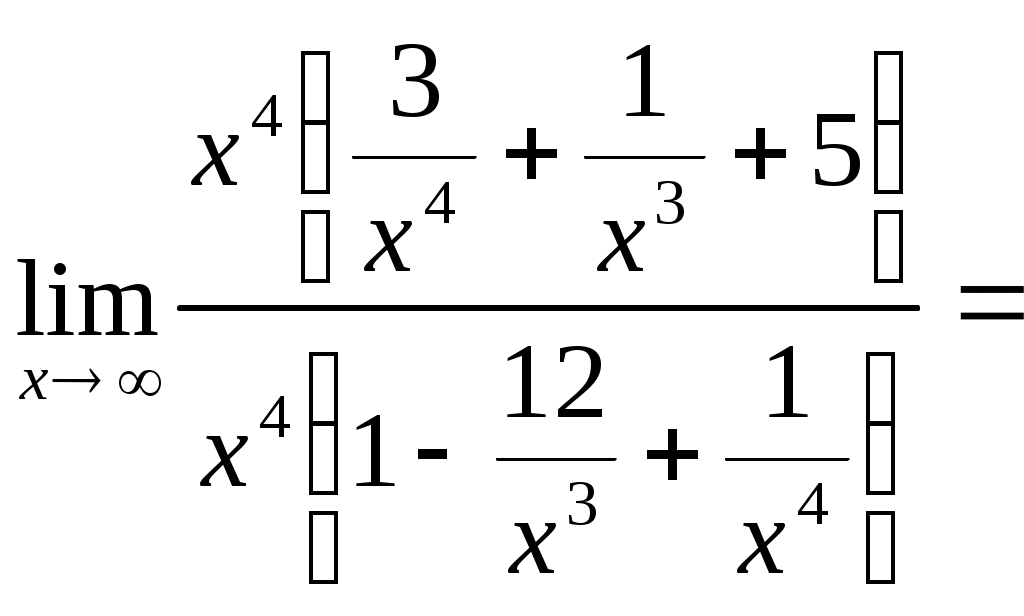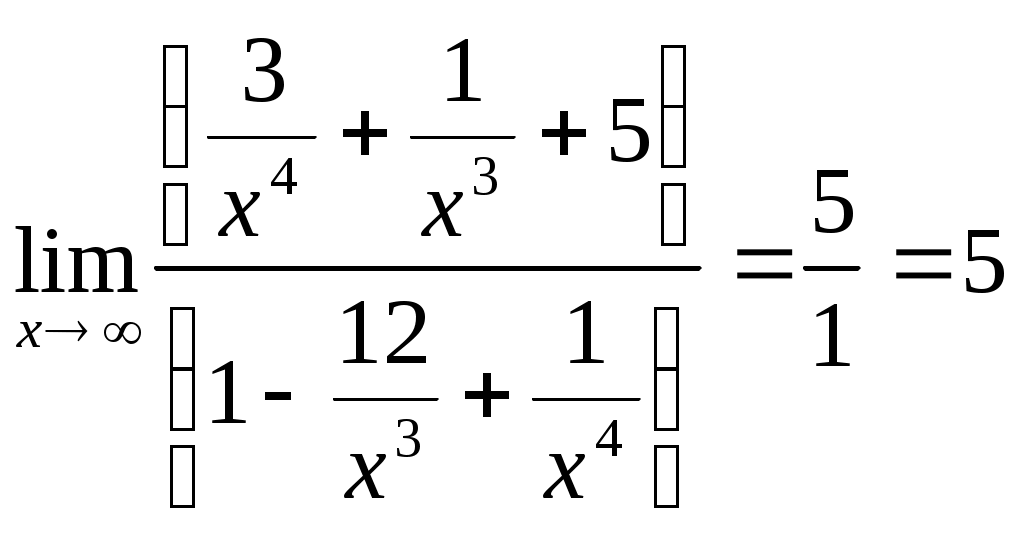. Чтобы раскрыть неопределенность вида , необходимо предварительно числитель и знаменатель дроби разделить на и применить основные теоремы о пределах и свойствах бесконечно малых величин:

.

Ответ: .
б) .

Решение:

Непосредственная подстановка предельного значения аргумента приводит к неопределенному выражению вида . Чтобы раскрыть неопределенность вида , необходимо помножить числитель и знаменатель функции на выражение, сопряженное числителю .

.

Ответ: .

в) .

Решение:

Непосредственная подстановка предельного значения аргумента приводит к неопределенному выражению вида 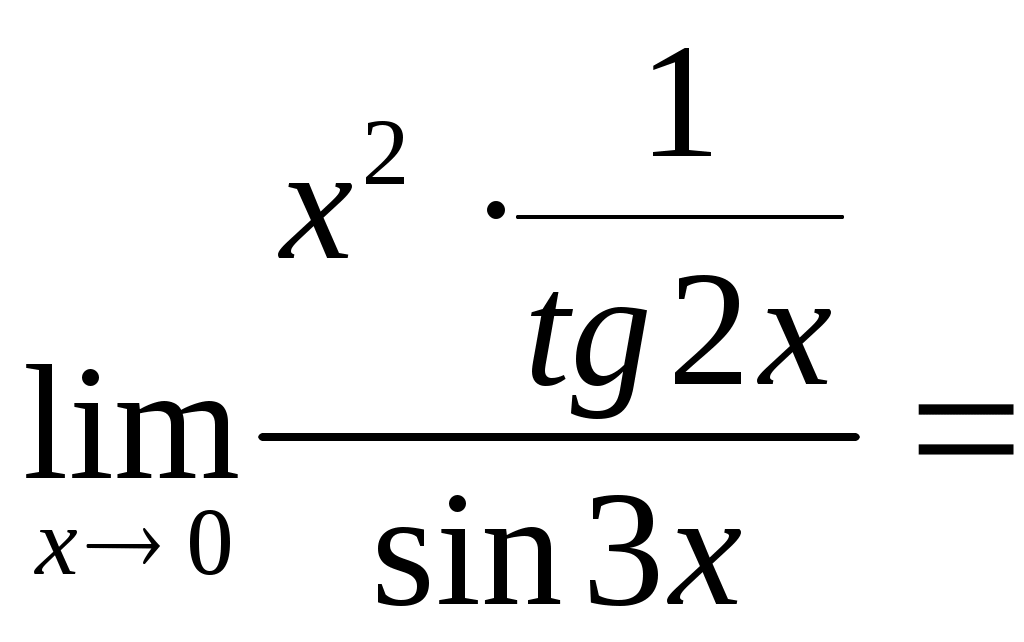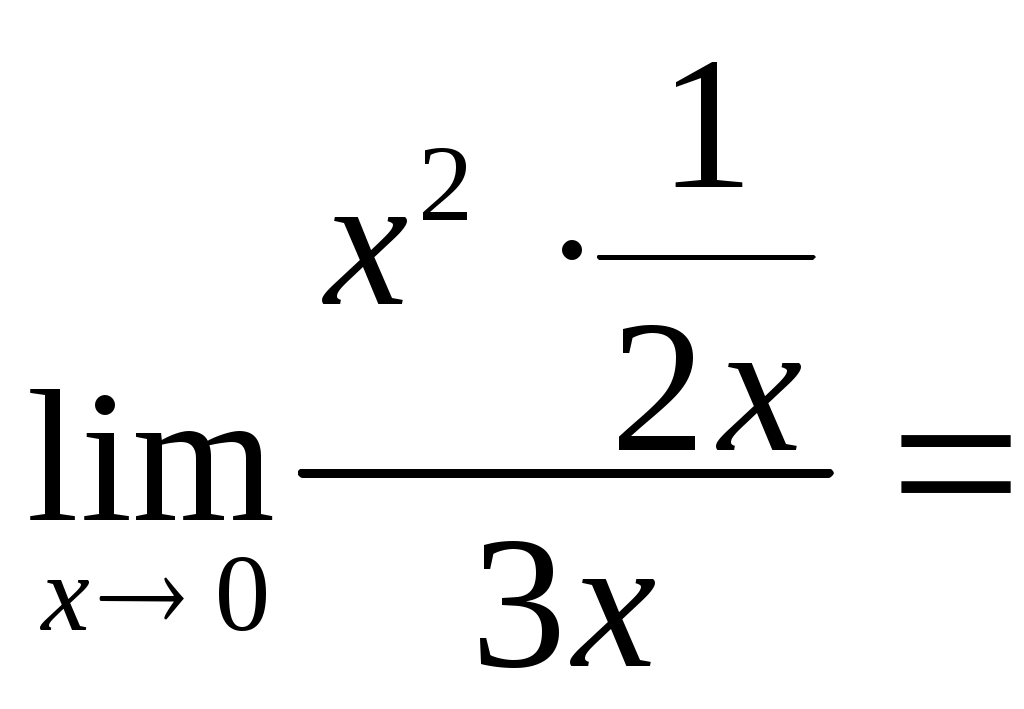. Чтобы раскрыть неопределенность вида , необходимо воспользоваться важнейшими эквивалентностями:



.

Ответ: .
г) .

Решение:

.

Пусть , тогда , при , .

Применим второй замечательный предел:

= = .

Ответ: .
51- 60. Заданы функция у = f(x) и два знамения аргумента . Требуется: 1) установить, является ли данная функция, непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разры­ва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.



Решение:

Функция   и неопределенна в т . Следовательно, в т.   разрыва нет, а т.   - точка разрыва. Т.к. 
, ,   и т.   не принадлежит области определения функции, то при   функция имеет точку разрыва второго рода (бесконечный скачок). Для схематического построения графика функции   найдем  . 

.
Построим график функции: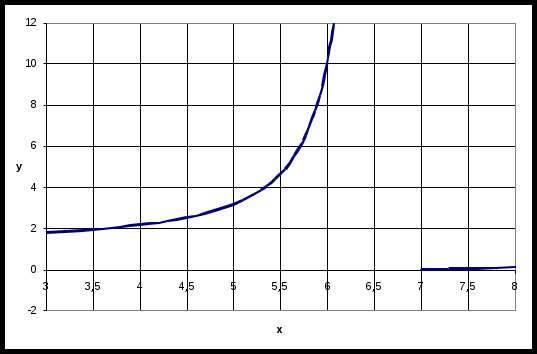


61-70. Найти производные dy/dxданных функций

а) .

Решение:

.

.
б) .

Решение:

.

.
в) .

Решение:

.

.
г) .

Решение:

Логарифмируем функцию:

;

;

Дифференцируем равенство по х:

.

.