Задачи для подготовки к егэ "Шар. Площадь поверхности шара"

• Название: Задачи для подготовки к егэ "Шар. Площадь поверхности шара"
• Дата: 26.12.2021
• Размер: 17.03 Kb.
• Имя файла: 000c7e94-de9675a8.docx
• Тип: Документы; #318418

Задачи для подготовки к ЕГЭ

"Шар. Площадь поверхности шара"

№1 Площадь большого круга шара равна 3. Найдите площадь поверхности шара.

№2 Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

№3 Ра­ди­у­сы двух шаров равны 6 и 8. Най­ди­те ра­ди­ус шара, пло­щадь по­верх­но­сти ко­то­ро­го равна сумме пло­ща­дей по­верх­но­стей двух дан­ных шаров.

№4Пло­щадь по­верх­но­сти шара равна 24. Най­ди­те пло­щадь боль­шо­го круга шара.

№5 Даны два шара с ра­ди­у­са­ми 5 и 1. Во сколь­ко раз пло­щадь по­верх­но­сти пер­во­го шара боль­ше пло­ща­ди по­верх­но­сти второго?

№6 Шар впи­сан в ци­линдр. Пло­щадь пол­ной по­верх­но­сти ци­лин­дра равна 18. Най­ди­те пло­щадь по­верх­но­сти шара.

№7 Около ко­ну­са опи­са­на сфера (сфера со­дер­жит окруж­ность ос­но­ва­ния ко­ну­са и его вер­ши­ну). Центр сферы сов­па­да­ет с цен­тром ос­но­ва­ния ко­ну­са. Об­ра­зу­ю­щая ко­ну­са равна  7 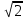 Най­ди­те ра­ди­ус сферы.

№8 Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.

Домашнее задание

№1 Пло­щадь боль­шо­го круга шара равна 1. Най­ди­те пло­щадь по­верх­но­сти шара.

№2 Дано два шара. Радиус первого шара в 60 раз больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

№3Радиусы двух шаров равны 32 и 60. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.

№4 Площадь поверхности шара равна 12. Найдите площадь большого круга шара.

№5 Даны два шара с ра­ди­у­са­ми 8 и 4. Во сколь­ко раз пло­щадь по­верх­но­сти пер­во­го шара боль­ше пло­ща­ди по­верх­но­сти второго?

№6 Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 6. Найдите площадь поверхности шара.

№7 Около ко­ну­са опи­са­на сфера (сфера со­дер­жит окруж­ность ос­но­ва­ния ко­ну­са и его вер­ши­ну). Центр сферы сов­па­да­ет с цен­тром ос­но­ва­ния ко­ну­са. Об­ра­зу­ю­щая ко­ну­са равна 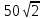  Най­ди­те ра­ди­ус сферы.

№8 Шар впи­сан в ци­линдр. Пло­щадь по­верх­но­сти шара равна 30. Най­ди­те пло­щадь пол­ной по­верх­но­сти ци­лин­дра.