задачи геометрия. Задачи по гиометрии. Задачи с решениями по геометрии Шар, радиус которого 13см пересечен плоскостью на расстоянии 12см от центра. Найдите площадь сечения
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
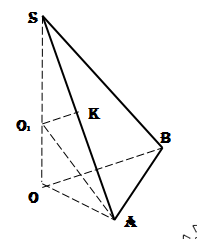
ΔSOA (∠SO1K=∠SAO, ∠SKO1=∠SOA=90°) ⇒ SO/SA=SK/SO1 ⇒ H/b=b/2R 100ballov.kz b2=2HR (Уравнение связи второе, пригод В основании пирамиды треугольник со сторонами 13см, 14 см, 15 см. Найти высоту пирамиды, если все высоты боковых граней 14 см. Высота боковой грани - апофема, строится из вершины пирамиды на ее грань. 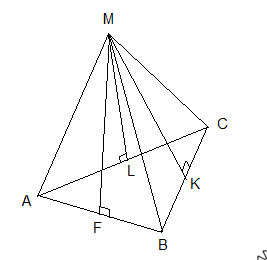 ABCM - пирамида. ABC -основание, угол B=90 ML, MK, MF - апофемы, по условию они равны (ML=MK=MF=14) H - высота Если все апофемы пирамиды равны, то в основание такой пирамиды можно вписать круг, а высота, опущенная из вершины на основание, падает в центр вписанного в основание круга. Следовательно точки L,K,F будут равноудалены от центра окружности O на радиус этой окружности, иными словами найдем сначала радиус вписанной окружности в основание пирамиды, затем исходя из того что углы KOM,LOM и FOM будут равны 90 градусов, по теореме пифагора найдем высоту. R=√[(p-a)(p-b)(p-c)/p]=√[(21-13)(21-14)(21-15)/21]=√16=4 142=42+H2 H2=14*14-4*4=180 H=√180=6√5 Диагональ параллелограмма делит его угол на две части в 60 и 45. Найти отношение сторон параллелограмма. Начнем с того что начертим этот параллелограмм.  Итак наш параллелограмм ABCD. BD - диагональ, что делит ∠B на ∠ABD=45° и ∠DBC=60°, получается что ∠B=60°+45°=105°, так как у параллелограмма противоположные стороны равны и параллельны, то ∠B=∠D, а ∠A=∠C=180°-∠B=180°-105°=75° Хорошо, это повторили, но найти отношение сторон довольно просто и для этого нужно всего лишь знать теорему синусов: 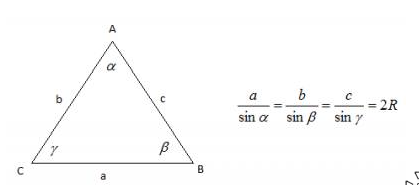 Как видишь, это легко применить к нашему примеру если рассматривать треугольник ABD, то пусть сторона AB будет a, AD - b, α=∠ADB=60°, β=∠ABD=45° Теперь остается лишь на тестировании запомнить таблицу синусов и косинусов. Зная это легко можно устно решать такие задачи и как я уже говорил пользование калькулятором совсем не обязательно. a/sin60°=b/sin45° a*sin45°=b*sin60° (a*√2)/2=(b*√3)/2 a√2=b√3 a/b=√3/√2 Основанием пирамиды является прямоугольник, диагональ которого 10 см. Каждое боковое ребро пирамиды равно 13см. Найдите высоту пирамиды. 52+H2=132 H=12 см Итак, высота падает на центр пересечения диагоналей основания пирамиды, то есть образуется прямоугольный треугольник, где ребро является гипотенузой, а высота вторым катетом!!! Основаниями а и b (a>b).Боковые ребра наклонены к плоскости основания под углом 60,Определить объем усеченной пирамиды, решал , решал, там с арифметикой не получается, помогите?  Так, во-первых, проведи в верхнем и нижнем основании диагонали (d1=а√2 и d2=в√2), ну и подучим диагональное сечение- трапецию, при этом углы при основании равны 60*, тогда Н=хtg60=х√3, отсюда х=Н/√3 а в√2=а√2-2х=а2-2Н/√3 в=а-√2Н/√3 Н=(а-в)√3/√2 V=1/3Н(S+s+√Ss)=√3(a+b)(a2+b2+ab)/3√2=√6(a3-b3)/6 Найдите площади боковой и полной поверхностей правильной треугольной усеченной пирамиды со сторонами основании 10 и 4см и боковым ребром 5см В основании пирамиды лежит треугольник, у которого стороны равны 10 см. Параллельно плоскости основания проведена плоскость, которая отсекает у пирамиды треугольник со сторонами 4 см, этот треугольник тоже будет равносторонним. Начертим рисунок, чтобы лучше воспринимать объяснение. 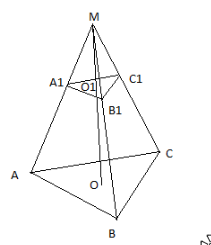 Итак, теперь мы видим усеченную пирамиду ACBA1B1C1, площадь боковой поверхности можно вычислить простым способом. Трапеция A1C1AC=C1B1CB=A1B1AB Зная стороны трапеции, мы легко найдем ее площадь, так как она равнобокая то найдем по формуле: Sтрап=(A1C1+AC)*H/2, где H - высота трапеции, в нашем случае определить высоту можно по формуле √(52-32)=√16=4 Sтрап=(4+10)*4/2=28 Sбок=28*3=84 Чтобы найти полную поверхность, нужно прибавить к боковой площади ее оснований. Sосн=(a2*√3)/4 Sосн1=(42*√3)/4=4√3 Sосн2=(102*√3)/4=25√3 Sполная=Sосн1+Sосн2+Sбок=4√3+25√3+84=29√3+84 В равнобедренном треугольнике боковая сторона равна 10 см., а основание 16 см., тогда высота опущенная на основание равна?  102-82=x2 x2=36 x=6 Численные значение объёма шара и площади поверхности шара равна. найти радиус шара? Vшара=Sшара Vшара=4πr3/3 Sшара=4πr2 4πr2=4πr3/3 r=3 Гипотенуза прямоугольного треугольника равна 18 см. чему равна медиана, проведённая к гипотенузе? Медиана - это линия, проведенная из вершины треугольника до противоположной стороны и делит ее пополам. 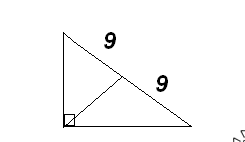 Медиана проведенная из прямого угла, равна половине гипотенузы. Через основание AD трапеции ABCD проведена плоскость а. Основание ВС нe лежит в плоскости α. Докажите, что прямая, проходящая через середины сторон АВ и CD, параллельна плоскости а. Все очень просто. Линия которая проходит через середины сторон АВ и CD называется средней линией, она параллельна обоим основаниям. Есть теорема о параллельности прямой и плоскости лежащей на прямой. Она говорит о том что любая плоскость лежащая на прямой, будет параллельна другой прямой параллельной данной. Проще говоря это и есть доказательство, почитайте теоремы о плоскостях и прямой. Дан треугольник ВСЕ. Плоскость, параллельная прямой СЕ, пересекает сторону BE в точке E1, а сторону ВС—в точке C1. Найдите длину отрезка ВС1, если C1Е1 :СЕ = 3:8, ВС = 28 см. Решается по подобию треугольников. Собственно BCE подобен BC1E1. Тогда составим простейшую пропорцию: 8 - 28 3 - x x=28*3/8=10.5 Точка Е не лежит в плоскости параллелограмма ABCD. Докажите, что прямая, проходящая через середины отрезков АЕ и BE, параллельна прямой CD. Треугольник ABE полученный из вершины E, средняя линия которого параллельна AB (средняя линия получается когда мы провели через середины отрезков АЕ и BE). Если AB параллельно средней линии, CD параллельно AB следовательно Средняя линия будет параллельна CD. В правильной четырехугольной усеченной пирамиде высота равна 2см,а стороны- 3см и 5см.Найти диагональ этой пирамиды. простая равнобедренная трапеция AB=3√2 CD=5√2 EF=AB, DE=FC=√2 BF=h=2 DF= 4√2 DBF: DB2=DF2+BF2=36 DB=6 Через сторону АС треугольника АВС проведена плоскость α(альфа). В принадлежит α(альфа). Докажите, что прямая, проходящая через АВ и ВС параллельна α(альфа). По условию сказано что сторона АС лежит на плоскости α (альфа), а это значит что точка A∈α, С∈α. Также тут говорится что B∈α а это значит что весь треугольник ABC построен на плоскости α. Следовательно любые прямые проведенные через две стороны будут принадлежать этой плоскости или будут ей параллельны. Дан треугольник МКР. Плоскость параллельная прямой МК пересекает МР в точке М1, РК в точке К1. Найти М1К1, если МР относится к М1Р как 12 к 5 (МР:М1Р = 12:5), а МК = 18 см Начнем с того что начертим рисунок.  Прямая M1K1 параллельна MK, это сделует из теоремы о плоскости и прямой, которая гласит: если прямая параллельная плоскости, то прямая построенная на этой плоскости будет параллельна первой прямой. Отсюда мы получим два подобных треугольника MKP и M1K1P Теперь дальше начнем размышлять исходя из подобия треугольников, мы можем записать следующее выражение: MK/M1K1=18/x ; где x - сторона M1K1 18/x=12/5 (согласно подобию по двум сторонам) x=7.5 Р лежит в плоскости трапеции АВСD. АD параллельна ВС. Доказать, что прямая, проходящая через середины РВ и РС параллельна Средней линии трапеции. Для начала вспомним что такое средняя линия, это линия которая соединяет половоны отрезков AB и DC. На рисунке я показал среднюю линию пунктиром.  Теперь мы поставили точку и провели линии к B и C. Получился треугольник, в котором половины сторон РВ и РС будут образовывать линию параллельную ВС, а как мы знаем средняя линия параллельна ВС, а значит и нашей прямой. точка P на рисунке лежит внутри трапеции, но если мы ее нарисуем за ее пределами, от этого не изменится решение! Середины сторон CD и BD треугольника BCD лежат в плоскости (альфа) а сторона ВС не лежит в этой плоскости. Докажите что прямая ВС и альфа параллельны. 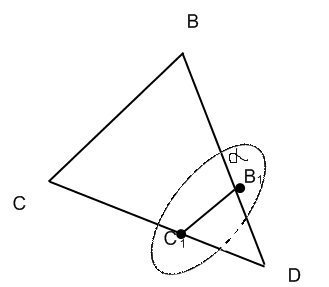 Прямая на рисунке C1B1 является средней линией треугольника BCD которая параллельна стороне CB. Если прямая СB паралельна прямой лежащей на плоскости альфа, то она будет параллельна самой плоскости. Основанием пирамиды является равносторонний треугольник, сторона которого равна 12 см. Каждое боковое ребро пирамиды образует с плоскостью основания угол 45 градусов. Найдите высоту пирамиды  ABC - равносторонний треугольник. BD является высотой равностороннего треугольника. Высота O1O, опущенная из вершины на основание ABC, падает в центр вписанного в основание круга. Если подумать то O1O = OD, так как угол OO1D равен 90 градусов, а угол O1DO равен 45 градусам. Найдем радиус вписанной окружности по формуле [√(3) * AB ]/6 [√(3)*12]/6=2√3 Основание пирамиды - ромб с диагоналями 6 м и 8 м, высота пирамиды проходит через точку пересечения диагоналей ромба и равна 1 м. Найдите боковую поверхность пирамиды.  На рисунке представлена пирамида ABCDS где S является вершиной и высота падает в центр O пересечения диагоналей основания ABCD. SK является апофемой. Для того чтобы найти площадь боковой поверхности необходимо сложить площади ΔABS, ΔADS, ΔDCS, ΔBCS. ΔABS=ΔDCS=ΔADS=ΔBCS, это следует из того что пирамида правильная, высота падает в центр пересечения диагоналей AC и BD, а стороны основания равны! Сначала найдем сторону основания ABCD, для этого вспомним что в ромбе половины диагоналей образуют прямоугольный треугольник. Отсюда AB=BC=DC=AD=√(42+32)=5 см. Так как треугольники ΔABS=ΔDCS=ΔADS=ΔBCS равны, то достаточно найти площадь одного из них и умножить все на 4. S(ΔDCS)=SK*DC=5*SK SK2=SO2+OK2 Точка K является центром описанной окружности вокруг треугольника COD. OK=радиусу этой окружности, и находится по формуле: S(ΔCOD)=3*4/2=6 OK=R=CO*OD*DC/4*S(ΔCOD)=4*3*5/4*6=60/24=2.5 SK2=12+2.52=1+6.25=7.25 SK=√7,25 S(ΔDCS)=SK*DC=5*√7,25 Sбок=5*4*√7,25=20*√7,25 Дано прямая четырехугольная пирамида. Диагональ основание 10см. боковое ребро 13 см. Найдите высоту пирамиды. Получается что у нас есть равнобедренный треугольник. Площадь его равна: √(p(p-a)(p-b)(p-c)), где p полупериметр равный 13+13+10=18 см. Теперь объясню зачем нам площадь такого треугольника понадобилась, дело в том что высоту можно будет найти исходя из формулы SΔ=a*h, где a - основание. √(p(p-a)(p-b)(p-c))=a*h √(18(18-10)(18-13)(18-13))=10*H H=60/10=6 см Основание пирамиды треугольник с катетами 6 и 8см. угол между боковой поверхностью и основанием составляет 60 градусов. Найдите высоту пирамиды. В основании этой пирамиды лежит прямоугольный треугольник. Найдем гипотенузу - √(6*6+8*8)=10 см.  Боковые грани одинаково наклонены к плоскости основания на угол 60 градусов, апофемы боковых граней равны, а это значит что основание высоты совпадает с центром вписанной окружности. Найдем радиус вписанной окружности а прямоугольный треугольник по формуле, можете записать пригодится: r= (a+b-c)/2, где a и b - катеты, c - гипотенуза. r=(6+8-10)/2=2 (один из катетов образованных прямоуг. треугольником с высотой h) Напротив угла 30 лежит сторона в 2 раза меньшая гипотенузе. Следовательно высота будет равна: h=√(4*4-2*2)=√12 В шаре радиуса 41 см на расстоянии 9 см от центра проведено сечение. Найдите площадь этого сечения)помогите не получается у меня с геометрией 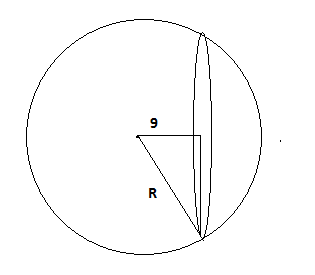 Итак сечением данным будет являться окружность, площадь которой равна Sсеч=πr2 Найди радиус такой окружности можно по теореме Пифагора, на рисунке показано как образуется прямоугольный треугольник. Итак r2=R2-92=1600 Sсеч=πr2=1600π |