задачи геометрия. Задачи по гиометрии. Задачи с решениями по геометрии Шар, радиус которого 13см пересечен плоскостью на расстоянии 12см от центра. Найдите площадь сечения
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
АВСА1В1С1 наклонная треугольная призма. двугранный угол при ребре ВВ1 равен 60 градусов, а расстояния от ребра ВВ1 до ребер АА1 и СС1 равны 1см и 2 см. Найдите площадь боковой поверхности призмы если ее высота равна 0,5 см а боковое ребро образует с основанием угол 30 градусов. Sбок=SAA1B1B+SBB1C1C+SAA1C1C AB=A1B1 , BC=B1C1 AA1=1, (по теореме: против угла 30 гр. лежит катет, равный половине гипотенузы) SAA1B1B=H*AB=0,5 кв.см SBB1C1C=H*BC=1 кв.см По теореме косинусов найдем сторону АС: AC=√(AB)Λ2+(BC)Λ2-2*AB*BC*cos60=√3 см SAA1C1C=H*AC=√3/2 кв.см Sбок=0,5+1+√3/2=(3+√3)/2 кв.см Отв: (3+√3)/2 кв.см АВСDА1В1С1D1 - прямоугольный параллелепипед, причем ВС=3а, СD=а,СС1=6а.Найдите тангенс угла между плоскостями ВС1D и АВС. Нам нужно найти тангенс угла между С1О и ОС : треуг АВС-прямоуг, АС=√(3а)Λ2+аΛ2=а√10см (по теореме Пифагора) ОС=0,5АС=(а√10)/2см , О-точка пересечения диагоналей основания; рассмотрим треуг.ОС1С-прямоуг. С1О=6а tgφ=C1C/OC=(6√10)/5 Основанием пирамиды является равносторонний треугольник. высота пирамиды равна 4 корня из 3.каждое боковое ребро образует с плоскостью основания угол 45 градусов. Найдите сторону основания пирамиды. Тут рисунок нужен. 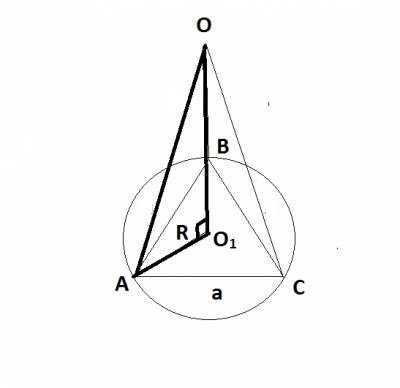 Получается что высота падает в центр равностороннего треугольника. Расстояние AO1 равно радиусу описанной окружности, а также равен высоте, так как угол составляет 45 градусов. Теперь вспомним формулу для нахождения стороны равностороннего треугольника из имеющейся описанной окружности. R=√(3)*a/3,где a - сторона основания. 4√(3) = √(3)*a/3 12=a, то есть a=12 В правильной четырехугольной пирамиде боковая поверхность равна 14,44 м в квадрате, а полная поверхность-17м в квадрате. Найдите сторону основания и высоту пирамиды. 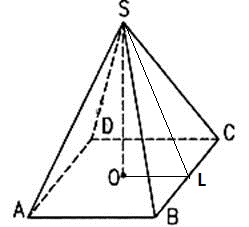 Sполн=Sосн+Sбок В основании ABCD лежит квадрат, так как она правильная четырехугольная пирамида. Sосн=a2=17-14.44 a2=2.56 a=1.6 SO - высота. Она найдется если найти SL и применить формулу Пифагора. Sбок=SL*a*4=14,44 SL*1.6*4=14,44 SL=3.61/1.6 Теперь чтобы найти высоту надо SL2=h2+OL2 (OL)2=(a/2)2=2.56/4 h2=(3.612/1.62)-(2.56/4) Стороны оснований правильной усеченной треугольной пирамиды 4 и 12 дм. боковая грань образует с большим основанием угол 60 градусов. Найдите высоту. 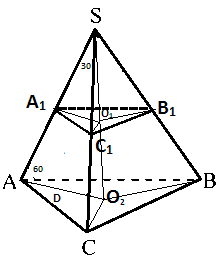 В пирамиде ABCS построим еще пирамиду A1B1C1S Так как пирамида правильная следует полагать что плоскости построенные на треугольниках ABC и A1B1C1 параллельны. А значит что пирамида ABCS подобна A1B1C1S. Тут идея простая если ∠BAC=∠ABS=60 градусов, то тогда получается что боковые грани AS,BS,CS пирамиды ABCS равны AB,BC,CA=12 дм. То же самое могу сказать про пирамиду A1B1C1S. Нам точно известно что A1B1,B1C1,C1A1=4 дм. (но это не понадобится) Итак для того чтобы найти высоту пирамиды ABCS - SO2 нужно обратить внимание на прямоугольный треугольник AO2S. ∠SAO2=60, а значит что угол ASO2=30. А напротив угла 30 градусов лежит сторона равная половине гипотенузы. AO2=12/2=6 Значит высота AO2 пирамиды ABCS = √(144-36)=√9*4*3=6√3 Теперь на чем основывается принцип подобия фигур? Если у нас пирамида ABCS подобная A1B1C1S имеет высоту равную 6√3, то другая будет иметь высоту во столько раз меньше, во сколько относятся стороны этих пирамид. Иначе говоря найдем коэффициент подобия фигур k=12/4=3 Значит что высота O1S=(6√3)/3=2√3 Получается что O1O2=6√3-2√3=4 Основанием пирамиды SABC служит треугольник, у которого АВ=ВС=20 с, АС=32 см; углы между плоскостью основания и каждой из боковых граней равны 45 (градусов). Найдите объем пирамиды 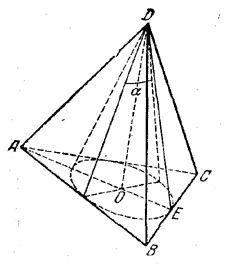 Пусть дана пирамида ABCD. В основание впишем окружность и найдем OE. ∠EOD=90, ∠OED=∠EDO=45 отсюда следует найдем EO найдем и высоту пирамиды. EO=Rвпис.окр=Sосн/p, где p - полупериметр. p=(40+32)/2=36 DO=Sосн/36 Потом по формуле V=(Sосн)2/3 Найдем площадь основания по формуле Sосн=a*h, где a-AC, h=12 (Правило идеальных треугольников в принципе если непонятно просто проведи высоту к стороне AC, затем найди эту высоту по формуле Пифагора, просто облегчают такие цифры решение как 20-16-12, 10-8-6, 5-4-3 это все треугольники прямоугольные с такими сторонами запутал наверное). Sосн=32*12=384 V=384*384/3=49152 Стороны прямоугольника относятся как 2:3.найдите отношение площадей основания тех цилиндров, боковая поверхность которых развертывается в такой прямоугольник. Довольно простая задача. Просто одна сторона у прямоугольника например 4π, а вторая значит будет равна 6π. При развертке цилиндра сторона которая будет равна длине окружности цилиндра. Т.е. 2πR=4π, отсюда R=2 S=4π теперь развернем по другому и получим 2πR=6π R=3, S=9π Получается что отношение площадей 9/4 Плоскость, паралл-ая оси цилиндра, пересекает основание цилиндра по хорде, составляющей с диагональю данного сечения угол бетта. Радиус осн.цилиндра, проведенный в один из концов хорды, образует с плоскостью сечения угол альфа. Высота цил.равна Н. Найти площ.осевого сечения. 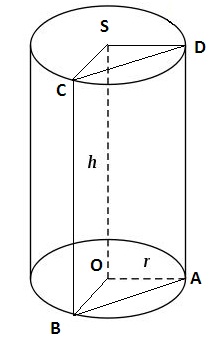 Сечение ABCD ∠DBA=β OA=OB=SC=SD=Rокр ∠SCB=α CD,BA – хорды Две параллельные плоскости α β пересекают сторону АВ треугольника АВС в точках D и D1,а сторону ВС-соответственно в точках Е и Е1. Найдите длину отрезка DЕ, если BD=12см,BD1=18, D1E1=54. 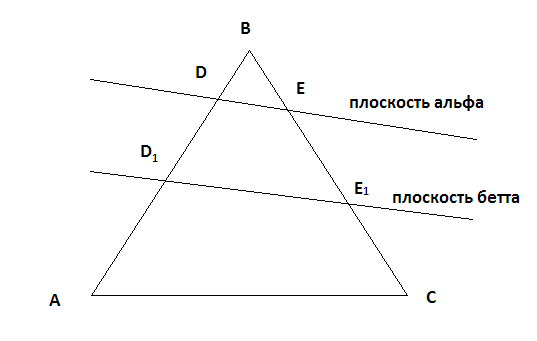 Никогда не забывайте. Что в результате пересечения двух параллельных плоскостей плоскостей, как показано на рисунке получаются два подобных треугольника BDE и BD1E1. А мы знаем уже что такое коэффициент подобия и поэтому легко найдем DЕ. k=18/12 k=D1E1/DE 18/12=54/DE DE=54*12/18=36 В основании наклонной призмы ромб с диагональю равной 24 см и стороной равной 37 см. Определите объём призмы, если перпендикулярное сечение, проходящее через большую диагональ ромба, имеет площадь равную 1400 см2.отв: 16800 см3 Большая диагональ равна 2* √(37*37-12*12)=2*35=70 H=1400/70=20 V=Sосн*H=(24*70/2)*20=16800 см3ъ Образующая конуса наклонена к плоскости основания под углом 30 градусов и равна 8. найти площадь осевого сечения конуса. 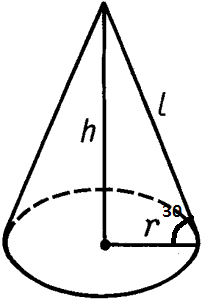 Отрезок, соединяющий вершину и границу основания, называется образующей конуса. Проще говоря l образующая. r - радиус. h - высота. Площадь осевого сечения равна h*d, где d=2r H=8/2=4 (Так как напротив угла 30 градусов лежит катет в два раза меньший гипотенузы l) Значит радиус равен √(64-16)=4√3 d=8√3 Sсеч=4*8√3=32√3 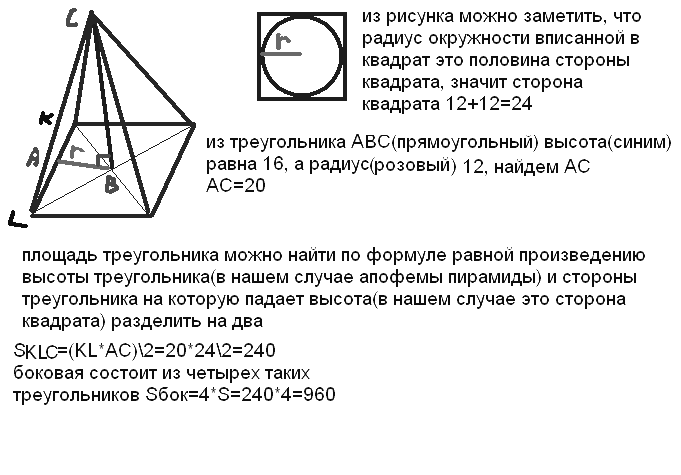 Высота правильной усеченной пирамиды равна 5 см. Стороны оснований составляют 8см. и 6см. Найдите боковое ребро пирамиды Боковое ребро можно найти. Для этого нужно найти радиус описанной окружности около каждого из оснований. Так как они являются равносторонними треугольниками сделать это будет не сложно. 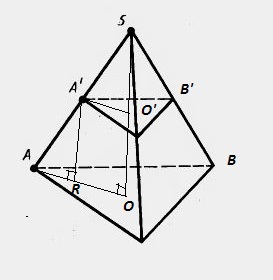 R=√(3)*a/3, где a - сторона треугольника. O'A'=R'=(6√3)/3 OA=R=(8√3)/3 A'R=H=5 AR=OA-O'A'=(2√3)/3 AA'R - прямоугольный с гипотенузой равной боковому ребру AA'. AA'=√[25+(4*3/9)]=√[25+4/3] дальше подстроить под ответ Длины высот треугольника равны 15, 21 и 35. Найти больший угол в градусах Наверное тут просто сделать так. Пусть всего в треугольнике сумма углов 180 градусов. Высоты относятся между с собой обратно пропорционально углам этого треугольника. То есть из вершины, которой проведена меньшая высота будет иметь больший угол. ha=15 hb=21 hc=35 a,b,c стороны треугольника. 15a=21b=35c=2S В конусе осевое сечение - правильный треугольник со стороной 2r. найти площадь сечения, проведенного через 2 образующие боковой поверхности, угол между которыми равен 30*.ответ:(r^2) 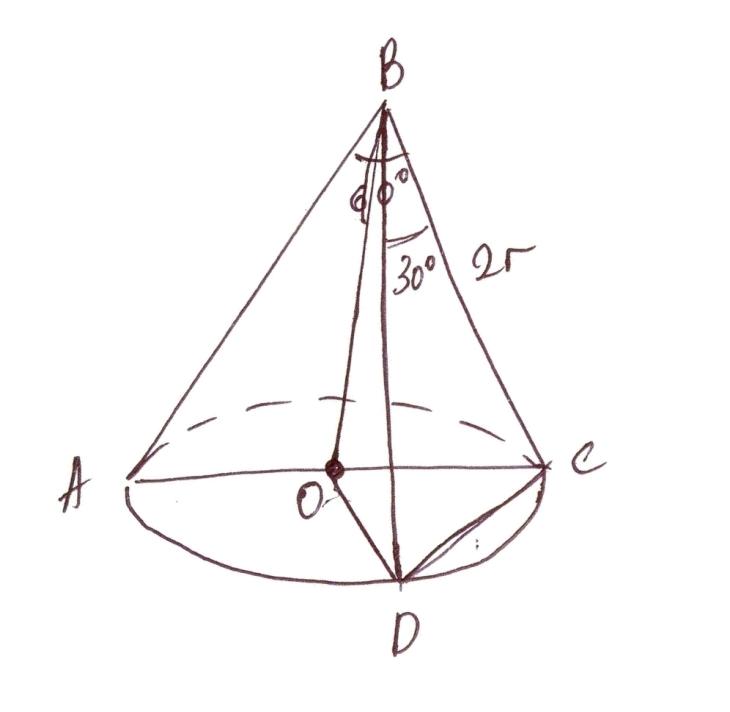 BC=2r BD=2r ∠DBC=30o S(BDC)=BC*BD*sin30/2 =2r*2r/4=r2 Высота конуса h, угол между высотой и образующей боковой поверхности равен 60*.найти площадь сечения, проведенного через 2 взаимно перпендикулярные образующие.ответ(2h^2) 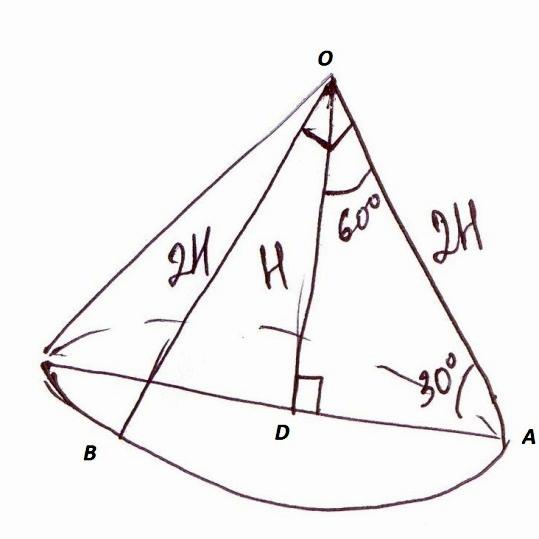 Если вспомнить то против угла 30 градусов лежит сторона в два раза меньшая гипотенузы. Значит образующая OA=OB равна 2H. Теперь по тому же принципу: SBOA=2H*2H*sin90o/2=2H2 Полукруг свернут в коническую поверхность. сколько градусов содержит угол между образующей и высотой конуса.  Пусть был круг радиусом R. Оторвали половину, свернули в конус. Получается что образующая DL стала равна R. А длина окружности при основании конуса стала равна дуге AB. дуга AB=2πR/2=πR Rкон=R/2 В два раза меньше гипотенузы, а значит равен угол 30 градусов. Прикрепления: 5768083.png(12Kb) Как доказать, что плоскость, касательная к конусу, перпендикулярна к плоскости, проходящей через образующую прикосновения и через ось конуса? У всякой плоскости, касательной к круговому конусу с вертикальной осью, горизонтальный след и образующая касания взаимно перпендикулярны. Высота конуса h, угол между высотой и образующей боковой поверхности равен 60 градусов .Найдите площадь сечения, проведенного через две взаимно перпендикулярные образующие!!!!!!! S=(1/2)h*c ( с-основание) Рассмотрим треуг., со сторонами-a, b, c: c=a1+b1 Угол между сторонами ( b, с)=180-(90+60)=30гр., тогда = (по теореме: против угла 30 градусов, лежит катет, =ый половине гипотенузы) b1=√(4hΛ2-hΛ2)=h√(3) ( по теореме Пифагора) b1/2=h/a1=b1/h=(h√(3))/h=√(3) (т.к. высота делит треуг. на два подобных треуг., то можно найти коэфф. подобия) h/a1=√(3) a1=h/√(3)=(h√(3))/3 c=(h√(3))/3+h√(3)=(4√(3)*h)/3 S=0,5*h*(4√(3)*h)/3=(2√(3)*hΛ2)/3 кв. ед. Высота конуса 6 см, а боковая поверхность 24Псм^2. определить объем конуса? Объем конуса составляет 48 см3. По формуле решил V=Sбок*H/3 Боковая поверхность конуса разрезана по его образующей и затем развернута так, что образовался круговой сектор. Определите радиус основания взятого конуса, если радиус полученного сектора равен 20см, а его центральный угол, составляет 45 , 60, 90сградусов. α - угол между радиусами. 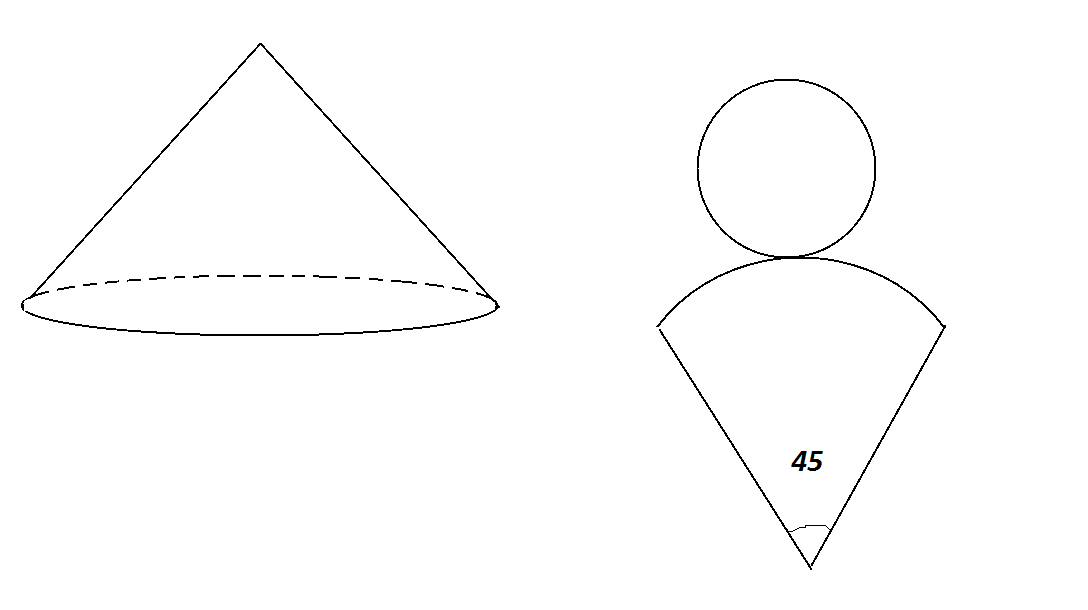 Я тут нарисовал что будет если разрезать такой конус. И как видишь длина такой дуги будет равна длине основания конуса и следуя из этого можно найти радиус основания конуса. Итак найдем длину дуги по формуле: L=2πR * (α/360o) 1) L=2π20**(45/360)=5π; 2πr=5π ⇒ r=2.5 (r - радиус основания) 2) L=2π*20*(60/360)=40π/6; 2πr=40π/6 ⇒ r=20/6 3) L=2π*20*(90/360)=10π 2πr=10π ⇒ r=5 Образующая конуса равна 20 см, площадь полной поверхности 400 кв.см. Найти угол развертки конуса. S=πRL+πR2=πR(R+ L), где L - образующая, r - радиус основания. А еще можно найти площадь по другому: S=πR2+Sсект Sсект - это и есть та развертка нашего конуса. Находится как Sсект=απR2/360 Где α- наш угол развертки. S=πR2[1+(α/360)] Площадь полной поверхности конуса равна S ,площадь осевого сечения q. Найти площ.основания конуса. Sполн=πR2+2πRH Sсеч=H*2R πR2=Sполн-2πRH 2πRH похоже на Sсеч только π не хватает. Добавим с двух сторон Sсеч*π=2πRH πR2=Sполн-Sсеч*π В шар вписана правильная четырёхугольная пирамида, все рёбра которой равны 12см. Вычислите радиус шара. Странно что ты не нашел решение, я уже решал эту задачу. Диагональ основания этой пирамиды будет равна диаметру шара. 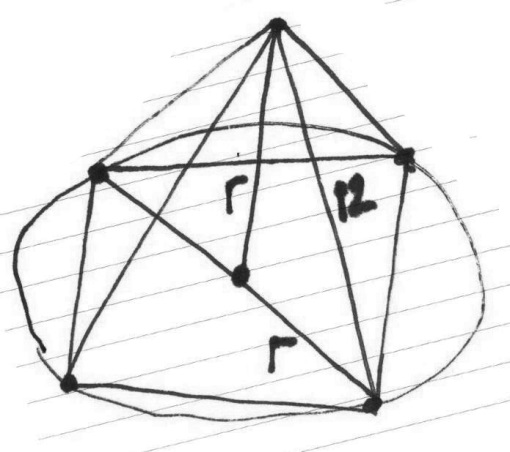 Центр шара лежит на высоте пирамиды и совпадает с центром окружности, вписанной в квадрат. 144=2r2 r=6√2 В конусе даны радиус основания R и высота H. Найдите ребро вписанного в него куба  OP=R SO=H O1P1=a, сторона куба вписанного в конус радиусом R и высотой H По подобию треугольников POS и P1O1S H /SO1 = R / P1O1 SO1=H-a P1O1 = a/√2. Является половиной диагонали основания куба и найдется так потому что угол у пересечения диагоналей равен 90 градусов. Теперь запишем это все как соотношение: H/(H-a)=R/(a/√2) Отсюда: Ha/√2 = RH – Ra Образующ. конуса 13 см, высота 12 см. Конус пересечен прямой, параллельной основанию; расстояние от нее до основания равно 6 см, а до высоты 2 см. Найдите отрезок этой прямой, заключенной внутри конуса. Радиус основания конуса равен 5, это стоит запомнить так как еще одна тройка Пифагора 5-12-13. 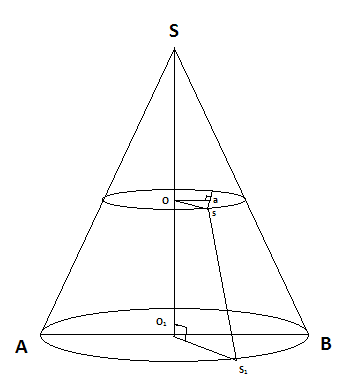 O1S1=Rкон По подобию k=SO1/SO=2, следовательно OS=R/2=2.5 2.52-22=a2, где a - длина нашего отрезка. Через точку О, лежащую между параллельными плоскостями альфа и бета, проведены прямые к и м. Прямая к пересекает плоскости альфа и бета в точках А1 и А2 соответственно, прямая м - в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1=12 см,В1О:ОВ2=3:4 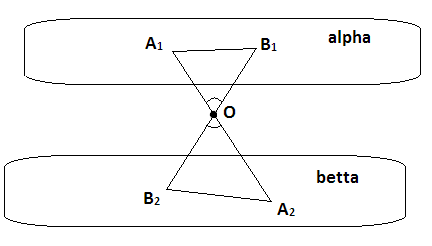 Тут все очень просто если вы знаете что они параллельны, ну плоскости, получается углы B2OA2 и B1OA1 равны между собой. А стороны A1B1 и A2B2 параллельны. Значит треугольники подобные и следовательно относиться стороны будут между собой В1О:ОВ2 = A1B1/A2B2 = 3/4 12/x = 3/4 x=4*12/3=16 В тетраэдре ДАВС угол ДВА=углуДВС=90 градусов, ДВ=6,АВ=ВС=8,АС=12. Постройте сечение тетраэдра плоскостью, проходящей через середину ДВ и параллельно плоскости АДС. Найдите площадь сечения. 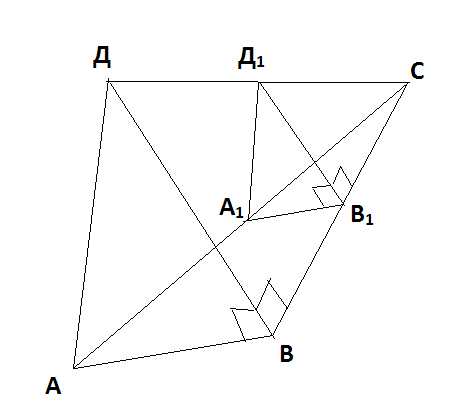 Практические идентичная задача, только тут всего лишь трудность построить такое сечение. Для начала выделите основные моменты. Именно в этой задаче еще раз придется вернуться к коэффициенту подобия k, который найдется из частного сторон подобных фигур. В общем это писалось неоднократно, и формулы простейшие. A1B1 - является средней линией равнобедренного треугольника ABC. Плоскости построенные на треугольниках ABД и A1B1Д1 параллельны. Следовательно треугольники ABД и A1B1Д1 подобные и притом все стороны A1B1Д1 вдвое меньше сторон ABД. Получается что Д1B1=ДB/2=3 A1B1=8/2=4 S(ΔA1B1Д1)=3*4/2=6 Все грани параллелепипеда АВСДА1В1С1Д1 прямоугольники, АД=4,ДС=8,СС1=6. Через середину ребра ДС параллельно плоскости АВ1С1 проведена плоскость .Найдите периметр сечения. 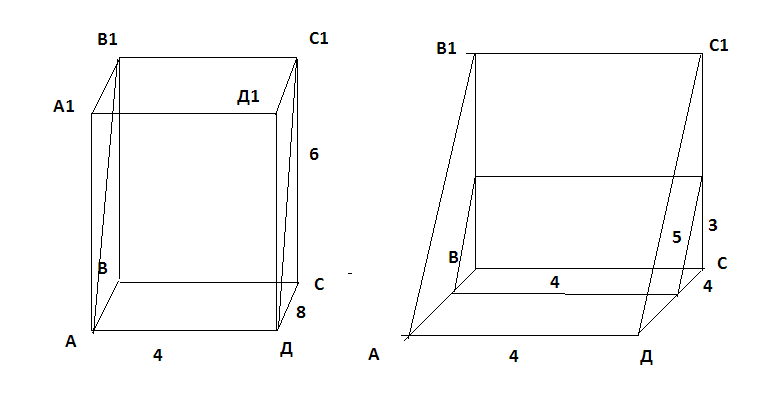 5*4=20 |
