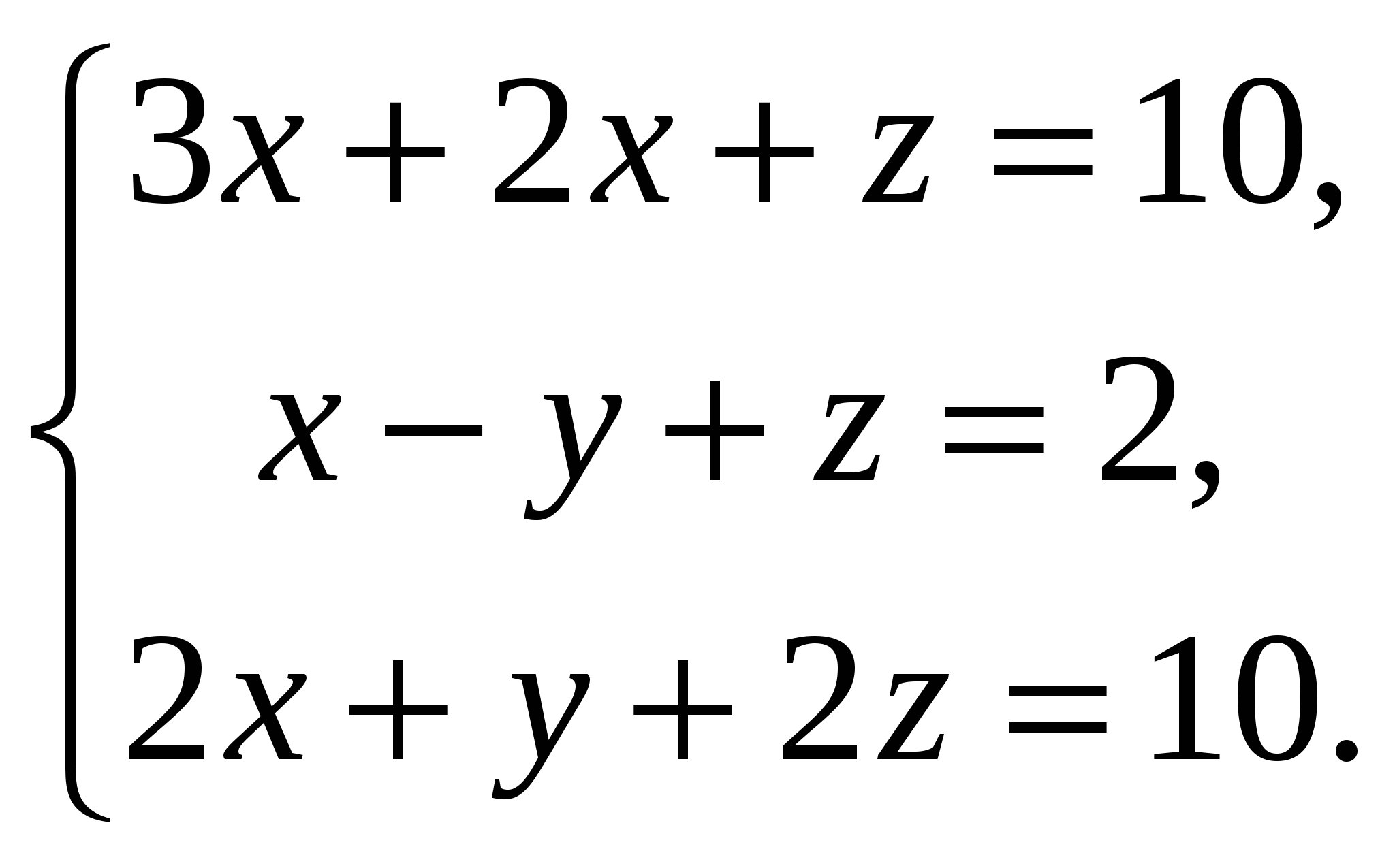вопросы на экзамен. Задачи и вопросы по курсу математики, 2014 г., первый семестр. ( лектор доц. Братчиков А. В.)
 Скачать 117 Kb. Скачать 117 Kb.
|
Задачи и вопросы по курсу математики , 2014 г., первый семестр . ( лектор доц. Братчиков А.В.)( три страницы )
Задача 24. Найти расстояние от точки М(0,1.-1) до плоскости 55x-22y-44z+88=0. Задача 25 Найти каноническое уравнение прямой, заданной системой уравнений 11x-66y+55z+99=0, 55x-22y-44z+88=0. Задача 26 Найти общее решение системы уравнений 11x-66y+55z+99=0, 55x-22y-44z+88=0. Задача 27. Найти центр и радиус окружности Задача 28. Вычислить векторное произведение вектора нормали к плоскости 11x +99y –111z-88=0 и направляющего вектора прямой (x-44)/33=(y-55)/22=(z-66)/77 Задача 29. Используя дифференциал, вычислить приближенно f (а+0,001) если известно значение f(a) (а- заданное число). Найти Задача 30 Найти точку пересечения прямой (задача 25) и плоскости x-y+z+9=0. Задача 31. Найти скалярное произведение векторов ортонормированном базисе Задача 32. Пусть ( лектор доц. Братчиков А.В.) ГЕОМЕТРИЧЕСКИЕ ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ. ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ. ДЕКАРТОВЫ КООРДИНАТЫ ВЕКТОРОВ И ТОЧЕК. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ. ОПРЕДЕЛИТЕЛИ 2-ГО И 3-ГО ПОРЯДКА. СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ. РАЗЛОЖЕНИЕ ОПРЕДЕЛИТЕЛЯ ПО СТРОКЕ ИЛИ СТОЛБЦУ. ОПРЕДЕЛИТЕЛИ n-ГО ПОРЯДКА. ОБРАТНАЯ МАТРИЦА. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. МАТРИЧНЫЙ СПОСОБ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. ПРАВИЛО КРАМЕРА. МЕТОД ГАУССА. ПРЯМАЯ НА ПЛОСКОСТИ. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ. ПРЯМАЯ В ПРОСТРАНСТВЕ. Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Координаты вектора. Метризация пространства. Скалярное произведение. Ортонормированный базис. Линейные операторы и действия над ними. Матрица линейного оператора. Собственные числа и собственные векторы матрицы. КОМПЛЕКСНЫЕ ЧИСЛА. ИЗОБРАЖЕНИЕ НА ПЛОСКОСТИ. МОДУЛЬ И АРГУМЕНТ. ТРИГОНОМЕТРИЧЕСКАЯ И ПОКАЗАТЕЛЬНАЯ ФОРМЫ КОМПЛЕКСНОГО ЧИСЛА. КОРЕНЬ ЦЕЛОЙ СТЕПЕНИ ИЗ КОМПЛЕКСНОГО ЧИСЛА. ПРЕДЕЛ ФУНКЦИИ.В ТОЧКЕ. СВОЙСТВА ФУНКЦИЙ ИМЕЮЩИХ ПРЕДЕЛ. ОДНОСТОРОННИЙ ПРЕДЕЛ ФУНКЦИИ. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ. 1-Й (с выводом) и 2-Й ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ. ТОЧКИ РАЗРЫВА. ПРОИЗВОДНАЯ ФУНКЦИИ. ЕЕ ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ. ДИФФЕРЕНЦИРОВАНИЕ ОБРАТНОЙ ФУНКЦИИ (НА ПРИМЕРЕ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ) . ТАБЛИЦА ПРОИЗВОДНЫХ. ДИФФЕРЕНЦИАЛ ФУНКЦИИ. ИНВАРИАНТНОСТЬ ДИФФЕРЕНЦИАЛА. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ (ФЕРМА,ЛАГРАНЖА, КОШИ) ПРАВИЛО ЛОПИТАЛЯ. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ [0/0], [∞/∞]. ЭКСТРЕМУМ ФУНКЦИИ. МОНОТОННОСТЬ НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ. ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ. ТОЧКИ ПЕРЕГИБА. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ. ЗНАТЬ МАТЕРИАЛ ВСЕХ ЛЕКЦИЙ И УМЕТЬ РЕШАТЬ ЗАДАЧИ РАССМОТРЕННЫЕ НА ПРАКТИЧЕСКИХ ЗАНЯТИЙ. |

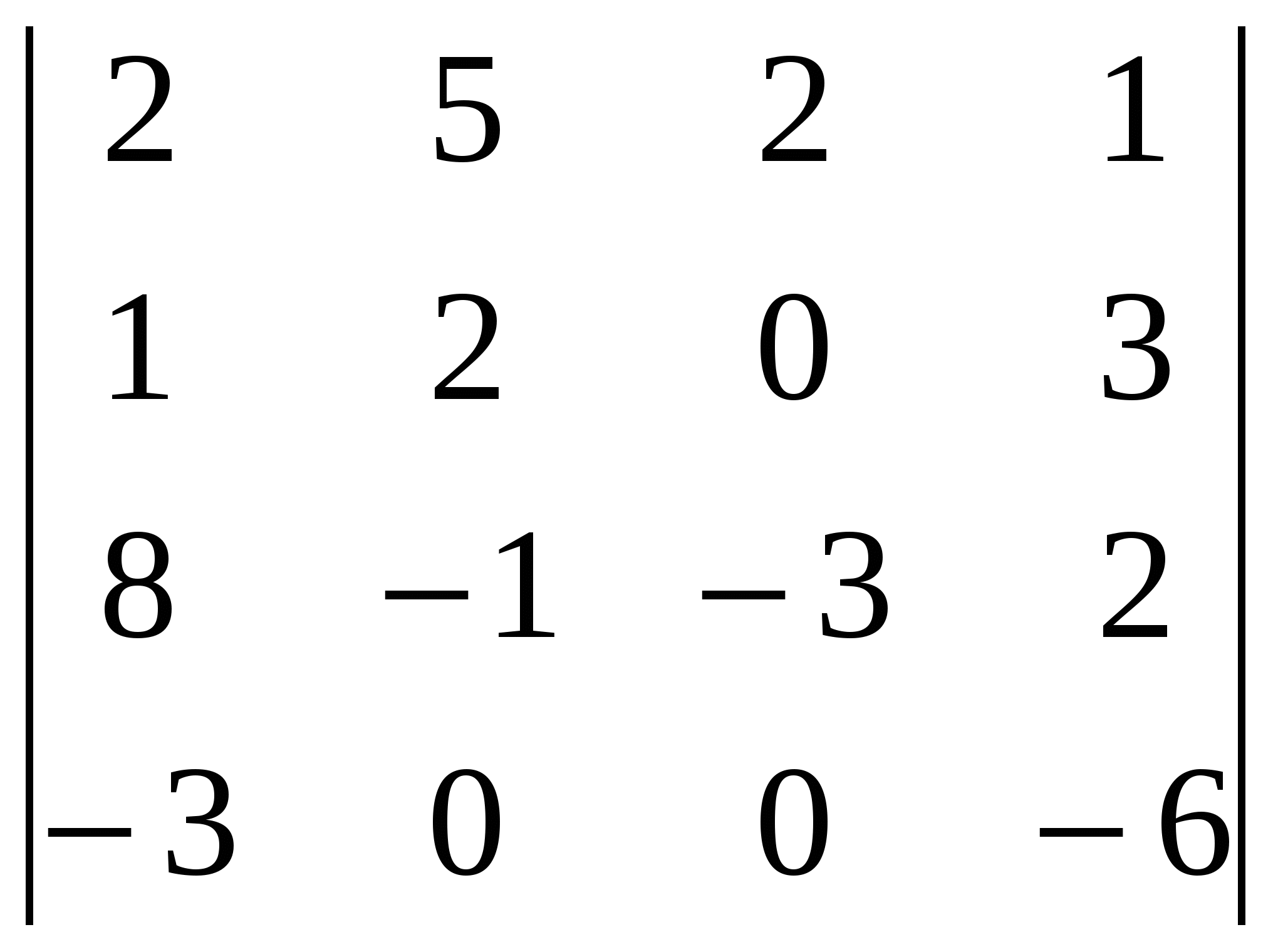 разложением по четвёртой строке.
разложением по четвёртой строке.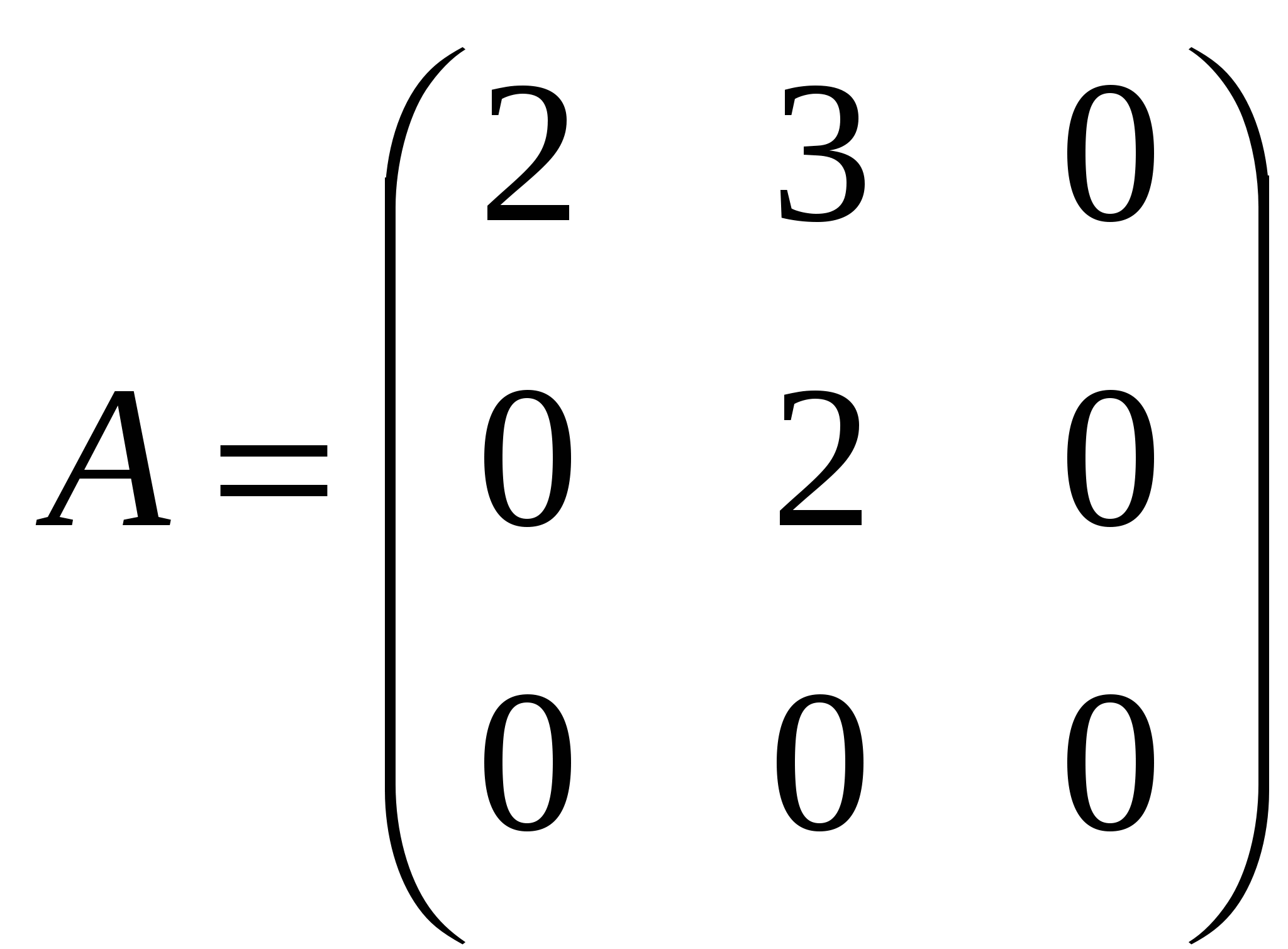 .
.