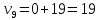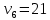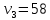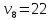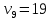идз №4. идз. Задачи индивидуального домашнего задания
 Скачать 271.36 Kb. Скачать 271.36 Kb.
|
ВЫПОЛНИЛ:
САНКТ-ПЕТЕРБУРГ
Задание: решить транспортную задачу в сетевой постановке методом потенциалов. Объемы производства и объемы потребления в транспортной, стоимости перевозки одной единицы однородного товара представлены на рисунке 1. 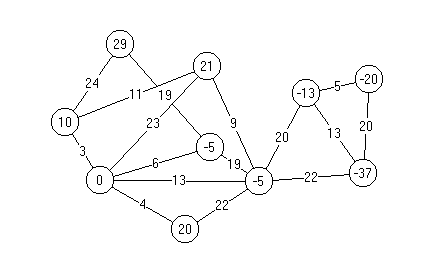 Решение: На рисунке 1 представлена транспортная сеть с десятью вершинами: пять пунктов производства, три пункта потребления и один перевалочный пункт. Представленная транспортная сеть является сбалансированной, так как суммарный объем пунктов равен нулю: ∑bi = 29+10+0-5-5+20-37-20-13+21 = 0 Построим начальный допустимый невырожденный поток по сети. Построение начального потока можно начать с любого пункта производства, например, как показано на рисунке 2.                   Рисунок 2 – Начальный поток по транспортной сети Построенный поток является допустимым невырожденным. Поток допустимый, так как выпускаемая продукция вывезена в полном объеме из пунктов производства, спрос полностью удовлетворен в пунктах потребления, а в перевалочных пунктах продукции не осталось. Поток невырожденный, так как перевозок получилось девять. Следует отметить, что при формировании начального потока по транспортной сети допустимое решение может оказаться вырожденным, то есть перевозок будет меньше, чем N-1. В этом случае одна или две вершины графа оказываются не задействованы перевозками, что приведет к их полному игнорированию в последующих итерациях. Поэтому вводят дополнительные перевозки, которые, во-первых, позволят быть решению невырожденным, а, во-вторых, свяжут все вершины графа. В прямоугольниках записаны объемы перевозимого продукта по коммуникациям. Значение целевой функции построенного потока будет равно: L1 = 10·3 + 29·19 + 21·9 + 19·24 + 33·20 + 5·20 + 37·22 + 22·20+10·13 = 3370 у.ед. Проверим начальный поток на оптимальность. Для этого пронумеруем вершины сети и рассчитаем потенциалы вершин в соответствии с правилом, представленным на рисунке 3, полагая, что   Рисунок 3 – Правило расчета потенциалов Для расчета потенциалов следует занумеровать вершины графа в произвольном порядке. Но далее от итерации к итерации эту нумерацию не менять. На рисунке 4 представлена транспортная сеть с рассчитанными потенциалами вершин.  Рисунок 4 – Транспортная сеть с рассчитанными потенциалами в первой итерации
Проверим построенный поток на оптимальность. Критерий оптимальности, следующий: поток через сеть оптимален тогда и только тогда, когда для всех коммуникаций выполнено следующее условие:  Невыполнение критерия оптимальности приводит к возникновению «невязок».  При проверке потока на оптимальность по формуле (1), становится очевидным, что критерий выполняется всегда на коммуникациях с введенными по ним перевозками. Поэтому стоит проверять выполнение критерия на тех коммуникациях, по которым не введены перевозки: (2;8) |29 - 22| = 7 <11 (1;8) |0 - 22| = 22 <24 (2;7) |29 – 25| = 4 <23 (7;9) |25 - 19| = 6 = 6 (7;6) |25 – 16| = 9> 4 – критерий не выполнен (3;5) |58 – 60| = 2 <13 (4;5) |63 – 60| = 3 <20 Имеется одна невязка на коммуникации (7;6), что говорит о существовании потока, доставляющего меньшее значение целевой функции. Величина «невязки» рассчитывается по формуле (2) и равна 9-4 = 5. «Невязка» единственная поэтому новую перевозку следует ввести по коммуникации (7;6).                                  Рисунок 5 – Новый поток по транспортной сети Значение целевой функции нового потока по сети будет равно: L2 =10·3 + 19·29 + 21·9 + 24·19 + 30·13 + 20·4 + 22·37 + 33·20+5·20 = 3270 у.ед.
(1;8) |0 - 22| = 22 <24 (1;8) |29 - 22| = 7 <11 (7;9) |25 – 19| = 6=6 (6;10) |21 - 38| = 17<22 (3;5) |58 – 60| = 2<13 (4;5) |63 – 60| = 3 <20 (2;7) |29 – 25| = 4 <23 В рассмотренном примере решение, полученное на второй итерации, оказалось оптимальным. Затраты на перевозку продукта составят 3270 у.ед. Ответ: минимальные затраты на перевозку однородного товара составляют 3270 у.ед., оптимальный план перевозок представлен на рисунке 5. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||