Задачи к контрольным заданиям. Задача см1

• Название: Задачи к контрольным заданиям. Задача см1
• Дата: 16.11.2022
• Размер: 3.87 Mb.
• Имя файла: Mekhanika_Metod_ukaz_B-EE_Chuba_Aleksandr_Iurevich_11633253.doc
• Тип: Задача; #791339

ВВЕДЕНИЕ
Внешние нагрузки, действующие на элементы сооружений, подразделяют на сосредоточенные и распределённые, статистические и динамические.

Статистические нагружают конструкции постепенно и меняются они во времени постоянно.

Динамические нагрузки изменяются значительно за малый промежуток времени.

Методы расчета элементов конструкций излагаются на основе следующих допущений: материал тела имеет сплошное строение; материал тела однороден и изотропен.

Для успешного изучения сопротивления материалов и выполнения контрольной работы, необходимо изучить следующие разделы:

1. Растяжение (сжатие).

2. Сдвиг и кручение.

3. Изгиб.

4. Напряжённое состояние в точке.

5. Гипотезы прочности.

6. Устойчивость элементов конструкции.

Каждый студент решает задачи входящие в состав контрольных работ по данным выбранным в соответствии со своим шифром. Каждая задача контрольной работы приведена в десяти типах и десяти вариантах.

Студент обязан взять тип схемы, который соответствует последней цифре шифра и из таблицы тот вариант с цифровыми данными, который соответствует предыдущей цифре шифра. Например, шифр 187892 - схема вторая девятого варианта.
Задачи к контрольным заданиям.

Задача 1.(СМ-1) Абсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой - 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке толчке. Требуется:

1) найти усилия и напряжения в стержнях, выразив их через силу F;

2) найти допускаемую нагрузку F_доп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ]=160 Мпа,(16кН/см²).

Данные взять из таблицы 1.

Таблица 1

Варианты	Данные величины					Варианты	Данные величины
	А, см2	а, м	b, м	с, м	Угол α, рад		А, см2	а, м	b, м	с, м	Угол α, рад
1.	10	2.1	3,1	1,0	π/4	6.	12	2,6	3,6	1,2	π/4
2.	10	2.2	3,2	1,0	π/4	7.	13	2,7	3,7	1,3	π/4
3.	11	2,3	3,3	1,1	π/4	8.	13	2,8	3,8	1,3	π/4
4.	11	2,4	3,4	1,1	π/4	9.	14	2,9	3,9	1,4	π/4
5.	12	2,5	3,5	1,2	π/4	10.	14	3,0	4,0	1.4	π/4

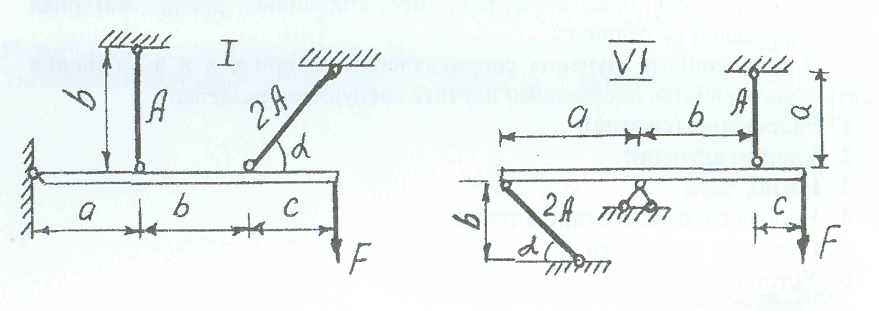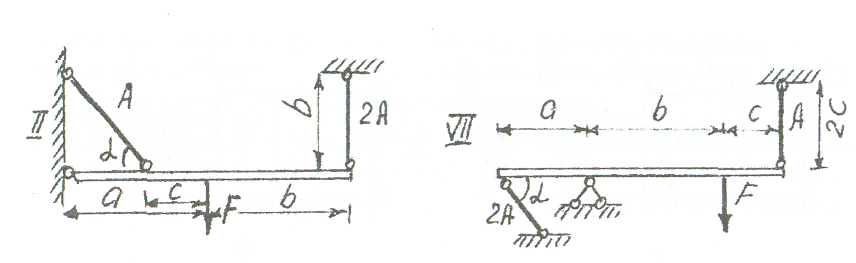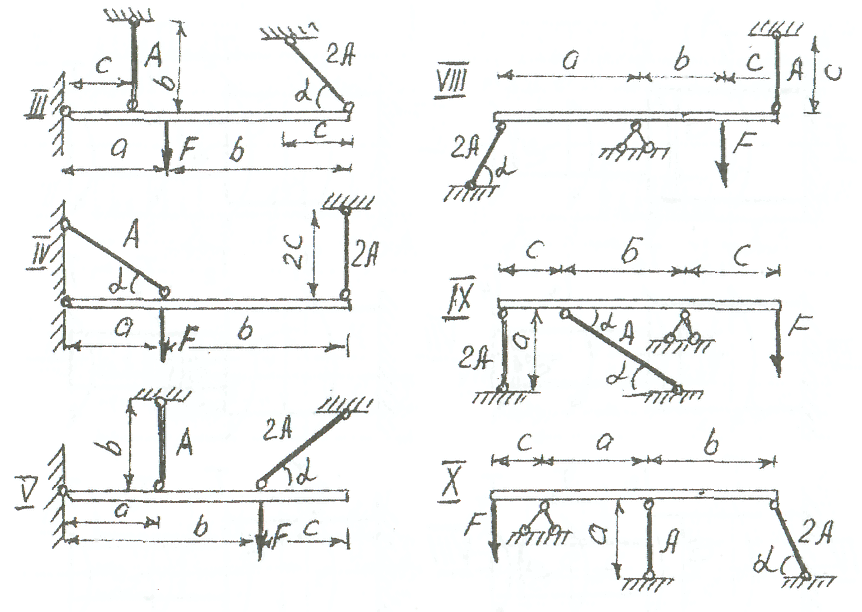Рис. 1
Указания. Для определения двух неизвестных усилий в двух неизвестных стержнях следует составить одно уравнение статики и одно уравнение деформаций.

Задача 2. (СМ-5) К стальному ступенчатому валу, имеющему сплошное поперечное сечение, приложены четыре момента (рис. 2). Левый конец вала жестко закреплен в опере, а правый конец - свободен и его торец имеет угловые перемещения относительно левого конца.

Требуется: 1) построить эпюру крутящих моментов по длине вала; 2) при заданном значении допускаемого напряжения на кручение определить диаметры d; и d₂ вала из расчета на прочность, полученные значения округлить; 3) построить эпюру действительных напряжений кручения по длине вала; 4) построить эпюру углов закручивания, приняв G≈0,4Е, (2*10⁴кН/см²). Данные взять из таблицы 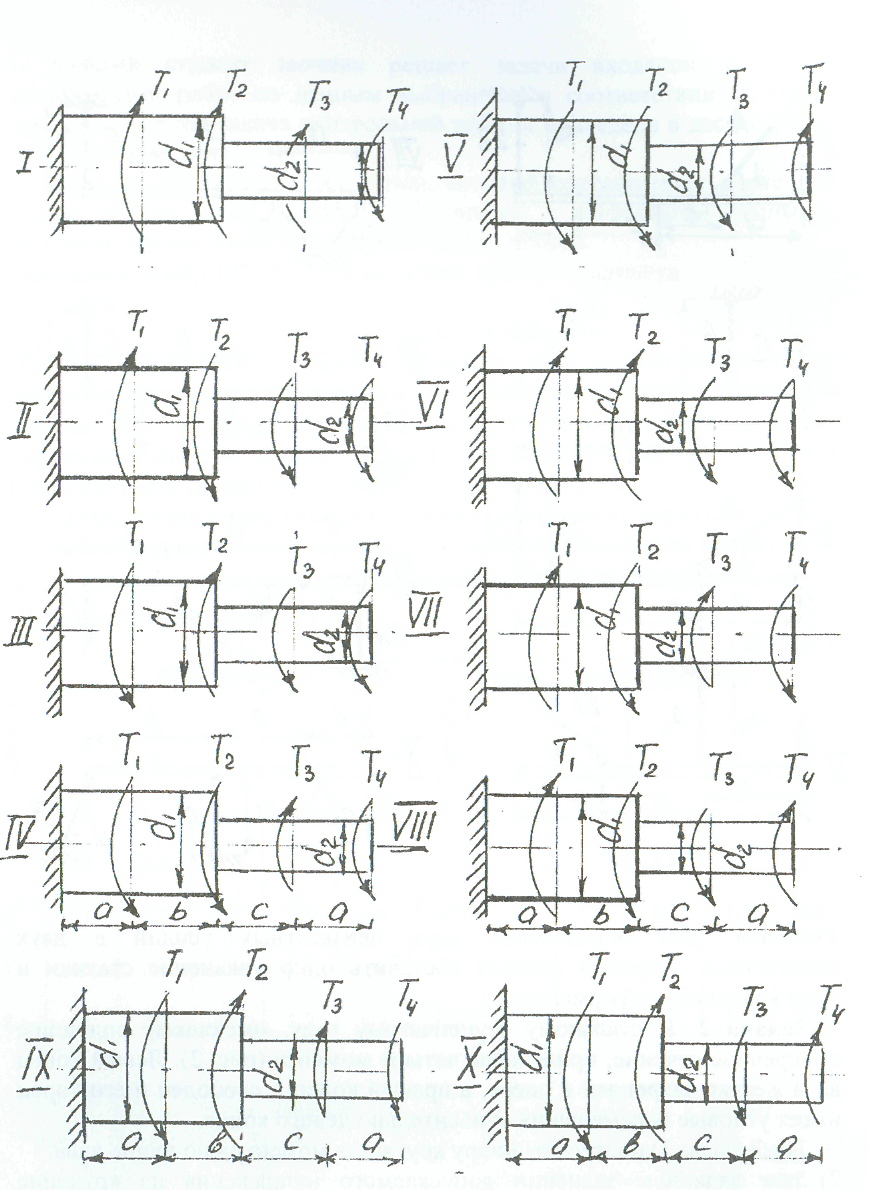2.

Рис. 2

Задана 3. (СМ-4) Для заданной схемы балки (рис.3) требуется построить эпюру поперечных сил и эпюру изгибающих моментов, найти максимальный изгибающий момент М_макс и по нему подобрать стальную двутавровую балку с указанием ее номера по ГОСТ 8239-72.

Допускаемое напряжение на изгиб принимать [σ]= 150Мпа.(15кН/см²). Данные для расчета взять из таблицы 3.

Некоторые значения моментов сопротивления сечения при изгибе W_x для балок двутаврового сечения (ГОСТ 8239-72) приведены (табл.3).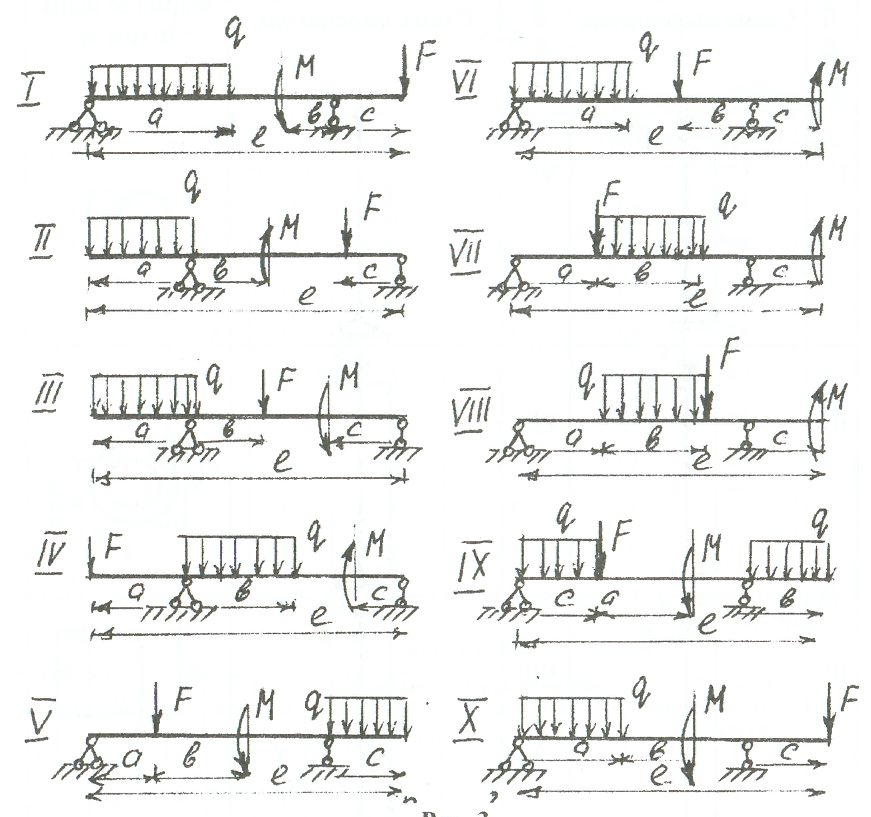



Рис.3
Задача 4. (СМ-6) Стальной стержень длиной L сжимается силой F (рис. 4). Стержень имеет различные схемы закрепления концов (два типа) и различные формы поперечного сечения (пять видов). Всего десять типов задач. Для схем I -V, коэффициент приведения длины μ = 2 / 3, для схем VI- X, μ = 1. Требуется:

1) найти размеры поперечного сечения при допускаемом напряжении [σ]= 160 Мпа (16кН/см²) (расчет производить последовательными приближениями, предварительно приняв величину коэффициента φ =0,5);

2) найти числовое значение критической силы и коэффициент запаса устойчивости. Данные взять из таблицы 4.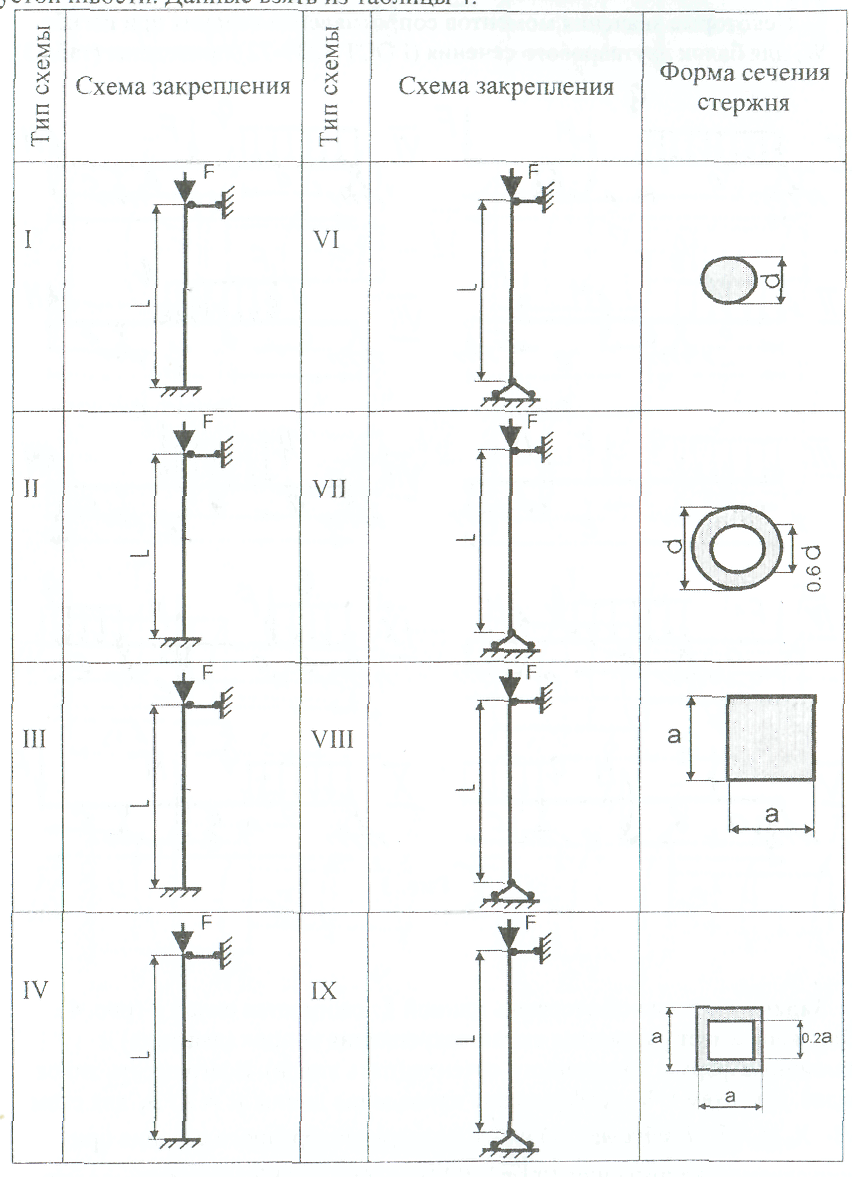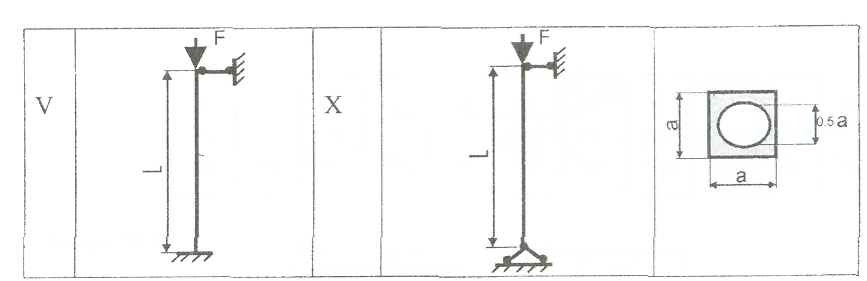





Рис.4

Таблица 2

Вариант	Расстояния, м				Моменты, кН*м				[τ],МПа
	а		b	с	T1	T2	T3	T4
1	1.0		1,0	1,0	5,1	2,1	1,1	0,1	30
2	1,1		1,1	1,1	5,2	2,2	1,2	0,2	30
3	1,2		1,2	1,2	5,3	2,3	1,3	0,3	35
4	1,3		1,3	1,3	5,4	2,4	1,4	0,4	35
5	1,4		1,4	1,4	5,5	2.5	1,5	0,5	40
6	1,5		1.5	1,5	5,6	2,6	1,6	0,6	40
7	1,6		1,6	1,6	5,7	2,7	1J	0,7	45
8	1,7		1,7	1,7	5,8	2,8	1.8	0,8	45
9	1,8		1,8	1,8	5,9	2,9	1,9	0,9	50
10	1,9		1,9	1,9	6,0	3,0	2,0	1.0	50

Таблица 3

Варианты	Данные величин
	а, м	b, м	с, м	1, м	Изгибающий момент М, кН* м	Сосредоточенная сила F, кН	Равномерно распределяемая нагрузка q, кН/м
1	2,0	3,2	1,8	10	7	20		22
2	2.2	3,4	1,9	10	7	19		21
3	2,4	3,6	2,0	11	8	18		20
4	2,6	3,8	2,1	11	8	16		19
5	2,8	4,0	2,2	12	9	15		18
6	3,0	4,2	2,3	12	9	14		17
7	3,2	4.4	2,4	13	10	13		16
8	3,4	4,6	2,5	13	10	12		15
9	3,6	4,8	2,6	14	11	11		14
10	3,8	5,0	2,7	14	11	10		13

Номер балки	10	12	14	16	18	20	22	24	27	30
Wx, см3	39,7	38,4	81,7	109	143	184	232	289	371	472

Таблица 4

Варианты	Данные величины
	F, кН	1. м
1 2 3 4 5 6 7 8 9 10	80 160 240 320 400 480 560 640 720 800	2,0 2,1 2,2 2.3 2,4 2,3 2,2 2,1 2.0 1.9

Примеры решения задач:

Задача №1

Абсолютно жесткий горизонтальный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров. Найти допускаемую нагрузку.

Дано:

А=10^-3 м² , с=1,0 м, а =2,2 м , α=45° , в =3,2 м.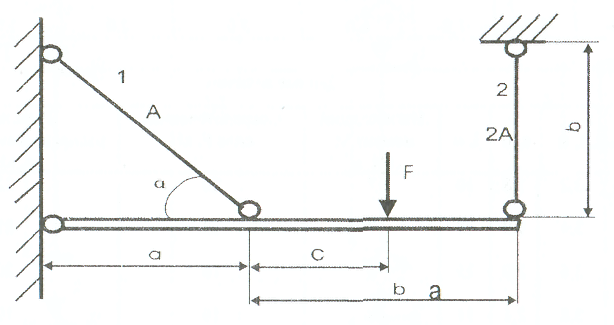



Решение: 1.

Найдем усилия и напряжения в стержнях, выразив их через F. Представим силовую схему и схему деформации системы. Из уравнения равновесия ΣМ₀ =0 (1).
N₂ *5,4-F*3,2 + N_l *sin45⁰*2,2 = 0 (1)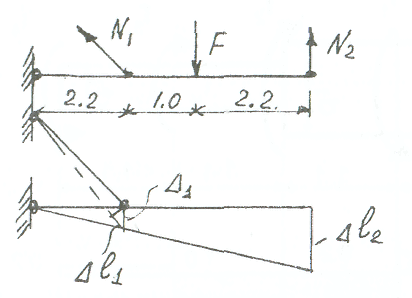



и условия совместности деформаций



используя закон Гука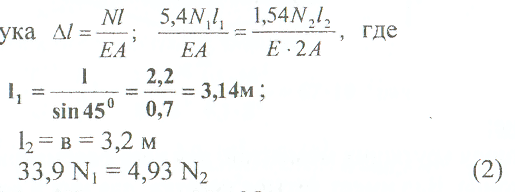

Решая совместно (1) и (2) находим N₁N₂: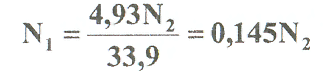



подставляем в (1)



Отсюда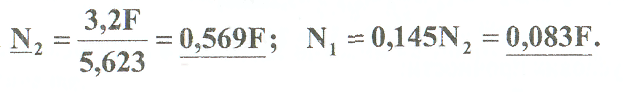

Находим напряжения в стержнях: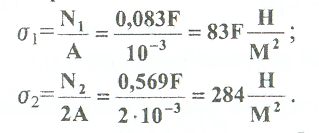



2.Найдём допускаемую нагрузку F_доп приравняв большее из напряжений в двух стержнях допускаемому напряжению[σ]=160 Мпа(16кН/см²). σ₂ =[σ]284 F_доп = 160-10⁶ F_доп =563,3KH (3)
Задача № 2

К стальному валу приложены четыре момента. Дано: а=1Лм; с=1,1м; Т₂ = 2,2кНм ; Т₄ = 0,2 кНм;

b = 1,1м; Т₁=5,2кНм; Т₃=1,2кНм; [τ] = 3 кН/см².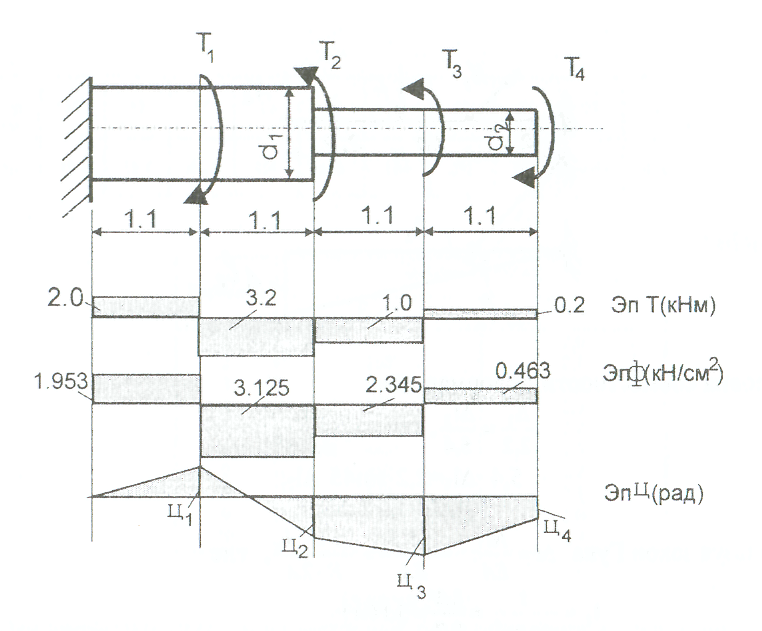

Решение: 1). Строим эпюру крутящих моментов, для чего рассматриваем вал со свободного конца. Вал имеет четыре участка, для них и составляем уравнение равновесия.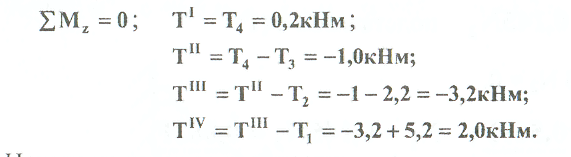

2). Исходя из условия прочности: Т„

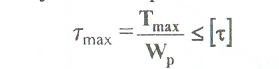(1), где

T_max - максимальный крутящий момент;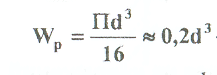
- полярный момент сопротивления.

Находим диаметры: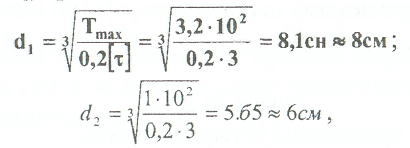



т.е. для первого и второго d₂⁼ 6см, для третьего и четвёртого d₁ = 8см. 3). Строим эпюру касательных напряжений: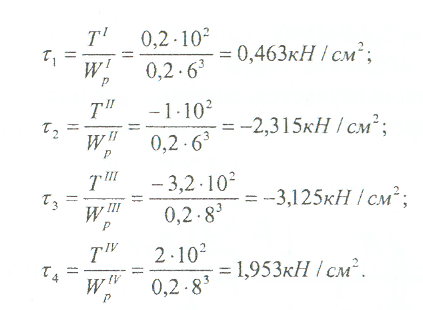



4). Строим эпюру углов закручивания приняв G = 0,4Е=8*10³ кН/см²

(2),

где Т - крутящий момент на участке,

G - модуль упругости при сдвиге,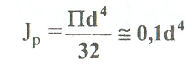

- полярный момент инерции.

Угол поворота начинаем определять от заделки.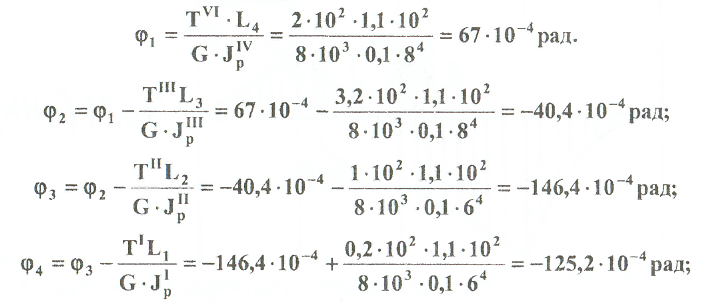

Полученные углы в масштабе наносим на эпюру ф, считая начало отсчёта в заделке.
Задача № 3

Для заданной схемы требуется подобрать стальную двутавровую балку.

Дано: а=2,2м, в=3,4м, с=1,9м, L=10,0м, М=7кНм, F=19kH,

q=21кН/м.

Решение:

1). Определяем реакции в опорах А и В из ур-й равновесия балки. Составим ΣМ_А=0.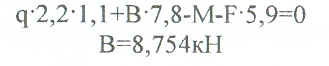



Составим: ΣМв⁼0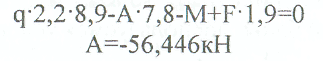



Проверяем правильность определения реакции:

A-q-2,2-F+B=0

56,446-46,2-19+8,754=0

Балка имеет четыре характерных участка, составим для них уравнения для определения поперечной Q силы и изгибающего момента М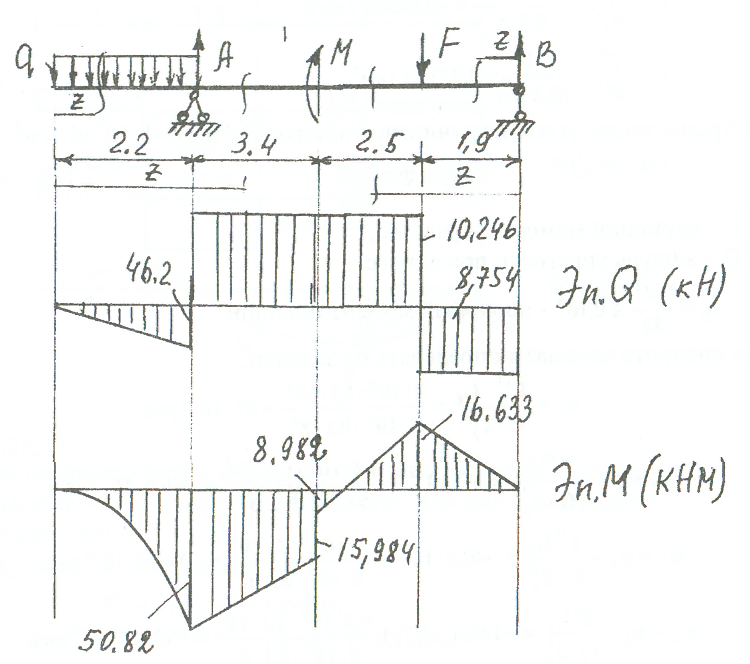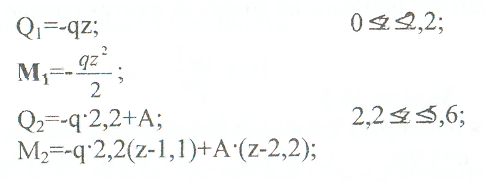


Q₁=-qz; 0 <z<2,2;
Q₂=-q-2,2+A; 2,2:Ј

M₂=-q-2,2(z-l,l)+A-(z-2,2);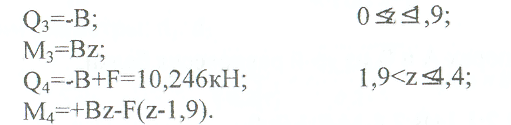



Q₃=-B; 0<£<1,9;

M₃-Bz;

Q₄=-B+F=10,246kH; 1,9

M,=+Bz-F(z-1,9).

После подстановки значений z полученные величины откладываем на эпюре «М», «Q».

Опасное сечение на левой опоре М_mах=50,82кНм. Для подбора двутавровой балки воспользуемся условием прочности (1).

Где [σ]=15кН/см из него находим момент сопротивления: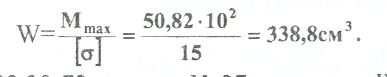



Выбираем по ГОСТ 82 39-72 двутавр № 27 имеющим W=371 см'. Определяем напряжение в нём (1).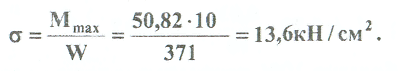



Отклонение 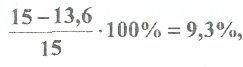что допустимо.
Задача № 4

Стальной стержень снимается силой F. Найти размеры поперечного сечения.

Дано: F=160кН, А=2,1м, [σ]=16кН/см².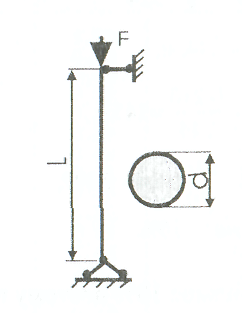



Решение:

1). Найдём размеры поперечного сечения по формуле (1)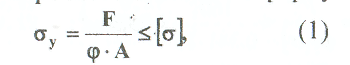



Где φ- коэффициент снижения допускаемого напряжения.

А- площадь поперечного сечения стержня.

Предварительно задаёмся φ=0,5 по (1) получаем: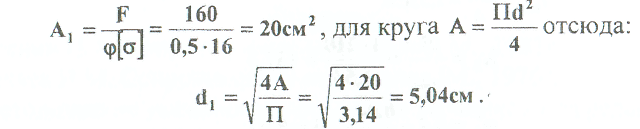

Определяем гибкость стержня по формуле (2)



где μ- коэффициент учитывающий способ закрепления концов.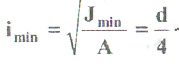

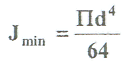- минимальный радиус инерции,
- минимальный момент инерции.

получим 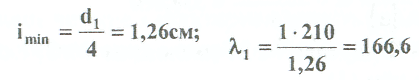по таблице 5

отыскиваем для λ₁, φ₁;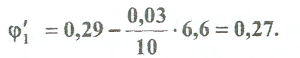

Разница между φ₁ и φ₁^/больше 10% поэтому повторим расчёт

2).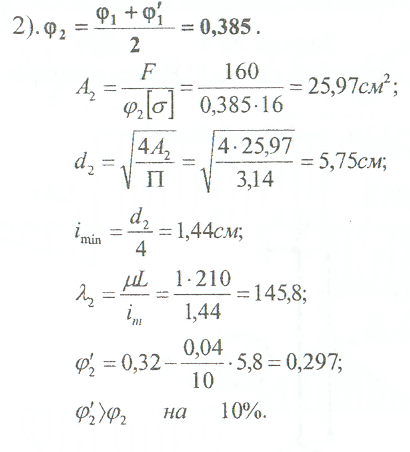

3). Разница между φ₂ и φ₂^/больше 10% поэтому повторим расчёт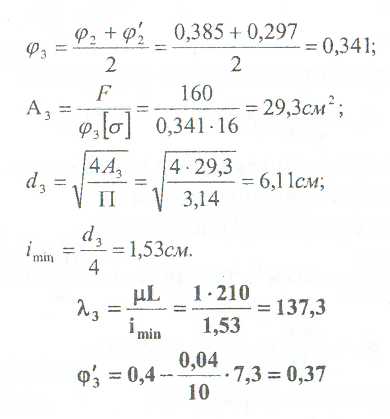



Определяем действительное нормальное напряжение: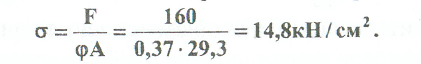

Недонапряжения 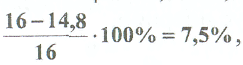что допустимо.

Так как λ₃ > λ_пр 137,3>100, то для определения критической силы используем формулу Эйлера.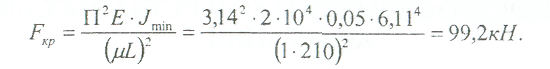



Коэффициент запаса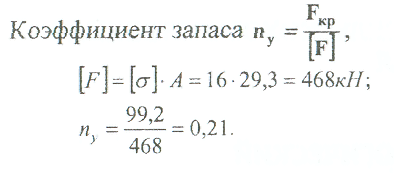
Таблица 5

Гибкость X	Стали: Ст. 1, Ст. 2, Ст 3, Ст. 4	Сталь Ст. 5	Сталь повышен­ного качества	Чугун	Дерево
0	1,00	1,00	1,00	1,00	1,00
10	0.99	0,98	0,97	0,97	0,99
20	0,96	0,95	0,95	0,91	0,97
30	0,94	0,92	0,91	0,81	0,93
40	0,92	0,89	0,87	0,69	0,87
50	0,89	0,86	0,83	0,57	0,80
60	0,86	0,82	0,79	0,44	0,71
70	0,81	0,76	0,72	0,34	0,60
80	0,75	0,70	0,65	0,26	0,48
90	0,69	0,62	0,55	0,20	0,38
100	0,60	0,51	0,43	0,16	0,31
110	0,52	0,43	0,35	—	0,25
120	0,45	0,37	0.30	—	0,22
130	0,40	0,33	0,26	—.	0,18
140	0,36	0,29	0,23	—	0,16
150	0,32	0,26	0,21	—	0,14
160	0,29	0,24	0,19	—	0,12
170	0.26	0.21	0,17	—	0,11
180	0,23	0,19	0,15	—	0,10
190	0.21	0,17	0.14	■—	0,09
200	0.19	0,16	0,13	—	0,08

Литература :

1. Стёпин П.А. Сопротивление материалов. М., 1983г.

2. Беляев Н.М. Сопротивление материалов. М, 1976г.

3. Методические указания для студентов заочников под редакцией П.Г. Гузенкова. М., 1984г.

4. Феодосьев В.И. Сопротивление материалов. М., 1974г.