Задачи приводящие к диф уравнению. Задачи, приводящие к диф уравнению. Задачи, приводящие к дифференциальному уравнению

• Название: Задачи, приводящие к дифференциальному уравнению
• Анкор: Задачи приводящие к диф уравнению
• Дата: 23.12.2021
• Размер: 305.5 Kb.
• Имя файла: Задачи, приводящие к диф уравнению.doc
• Тип: Реферат; #315984

ГАПОУ Орский индустриальный колледж г. Орска Оренбургской области

РЕФЕРАТ
На тему:
Задачи, приводящие к дифференциальному уравнению

Выполнил:

студент 2 курса

группы ИСа

Купцов Д. А.

Проверил:

преподаватель

Ибрачева Э. И.

Орск, 2021

СОДЕРЖАНИЕ

Введение………………………………………………………………………..2

1.Дифференциальные уравнения первого порядка

с разделяющимися переменными……………………………………3

2.Линейные дифференциальные уравнения первого …………..6

порядка……………………………………………………………….

3.Дифференциальные уравнения второго порядка…………..9

ВВЕДЕНИЕ

Математическое описание самых разнообразных явлений, происходящих в природе, часто приводит к уравнениям, связывающим независимую переменную, искомую функцию (одной переменной) и производные этой функции. Такого рода уравнения называют обыкновенными дифференциальными уравнениями. (В дальнейшем будем называть их дифференциальными уравнениями). Если в дифференциальное уравнение входит только независимая переменная, функция и её первая производная, то уравнение называется дифференциальным уравнением первого порядка.

В общем виде его можно записать так:

если оно решается относительно производной, то его можно записать так:

Если дифференциальное уравнение содержит ещё и производную второго порядка от искомой функции, то оно на- зывается дифференциальным уравнением второго порядка:



Основную трудность при решении задач, приводящих к дифференциальным уравнениям, представляет составление самих дифференциальных уравнений. Здесь нет универсального метода. Каждая задача требует индивидуального подхода, основанного на глубоком понимании соответствующего закона физики, химии, зоологии, биологии и умение переводить эти задачи на математический язык.


1. Дифференциальные уравнения первого порядка с разделяющимися переменными.
Задача 1. Найти закон движения свободно падающего в пусто-

те тела, если пройденный путь начинает отсчитываться от момента времени t = 0 и начальная скорость падения равна нулю. Скорость в этом случае выражается, как известно, формулой .
Решение.

Скорость переменного движения есть производная по времени. Поэтому =gt (1.1)

Из этого уравнения следует, что функция s есть первообразная функции gt. Следовательно, или (1.2)

Для определения произвольной постоянной С используем то условие, что начало отсчёта пути совпадает с началом отсчёта времени, то есть при t = 0 s = 0. Подставляя эти значения в равенство (1.2), находим 0 = 0+С, то есть С = 0, и следовательно, окончательно получаем .

Задача 2. (Об охлаждении тела). Скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Температура воздуха равна 20⁰С. Известно, что в течение 20 минут тело охлаждается от 100 до 60⁰С. Определить закон изменения температуры тела в зависимости от времени t.
Решение.

Согласно условию задачи имеем или

(1.3)

где k>0 – коэффициент пропорциональности и x = - 20.

Разделяя в уравнении (1.3) переменные и затем, интегрируя, получаем

,

что после потенцирования даёт .

Для определения С используем начальное условие x = 80 при

t =0: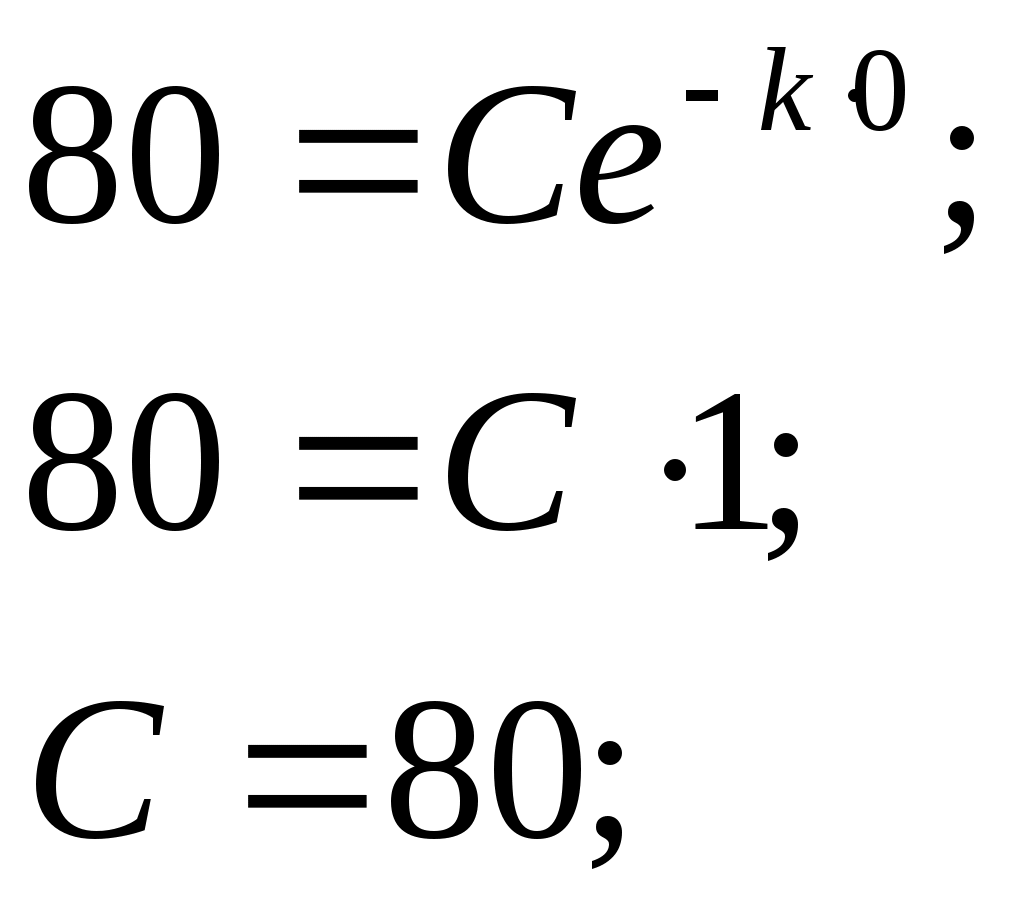



Следовательно, или откуда

Коэффициент пропорциональности k определяем из дополни - тельного условия: при t = 20, = 60. Отсюда 60=20+80 или

= и, следовательно, .

Итак, искомая функция .

Задача 3. (О движении моторной лодки). Моторная лодка движется в спокойной воде со скоростью . На полном ходу её мотор выключается и через 40 с после этого скорость лодки уменьшается до Сопротивление воды пропорционально скорости движения лодки.

Определить скорость движения лодки через 2 мин. после остановки мотора.
Решение.

На движущуюся лодку действует сила сопротивления воды

,

где >0 – коэффициент пропорциональности.

С другой стороны по второму закону Ньютона

и, значит, или .

Решим это дифференциальное уравнение, разделяя переменные и интегрируя, получим: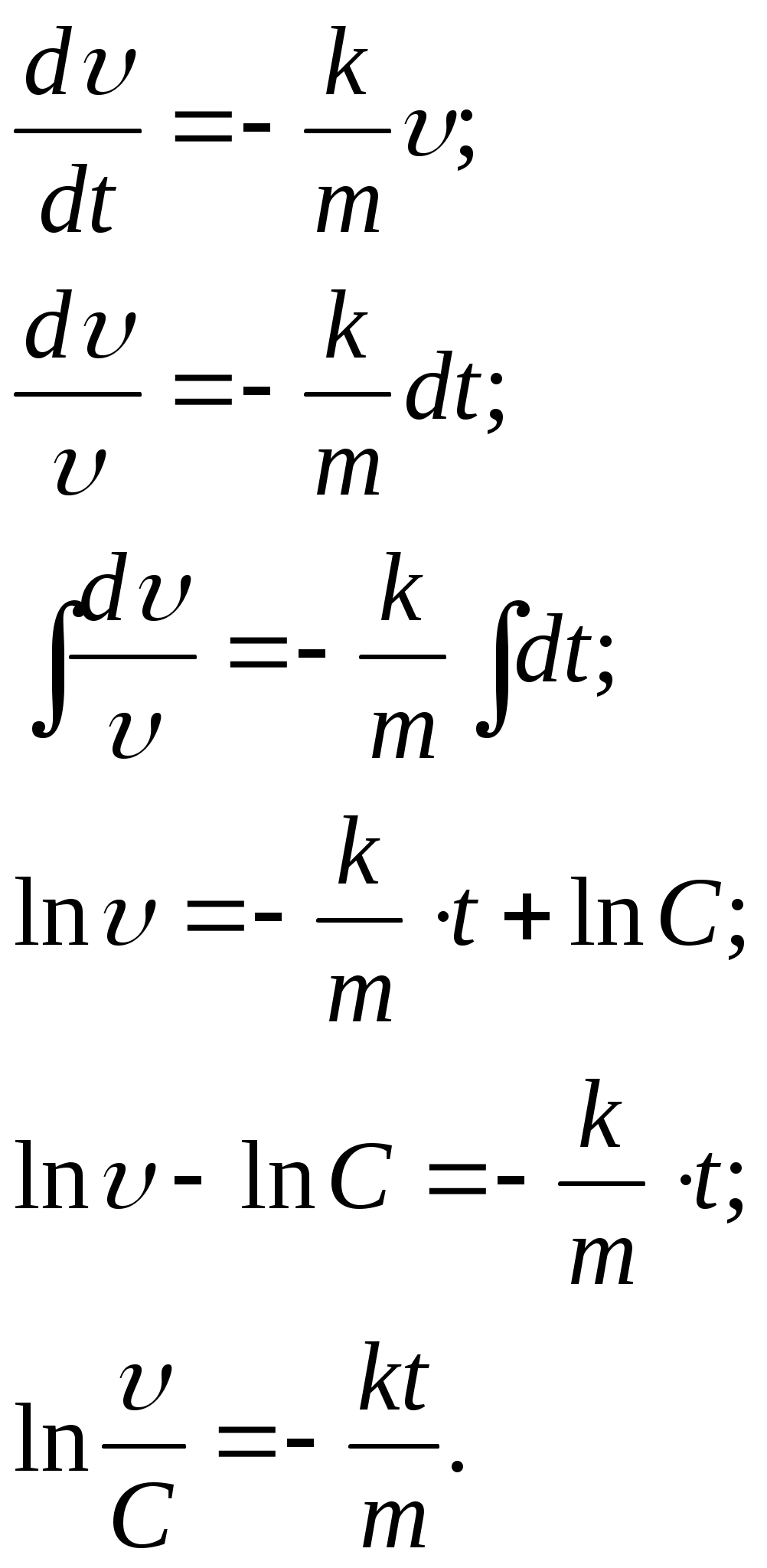



После потенцирования получаем: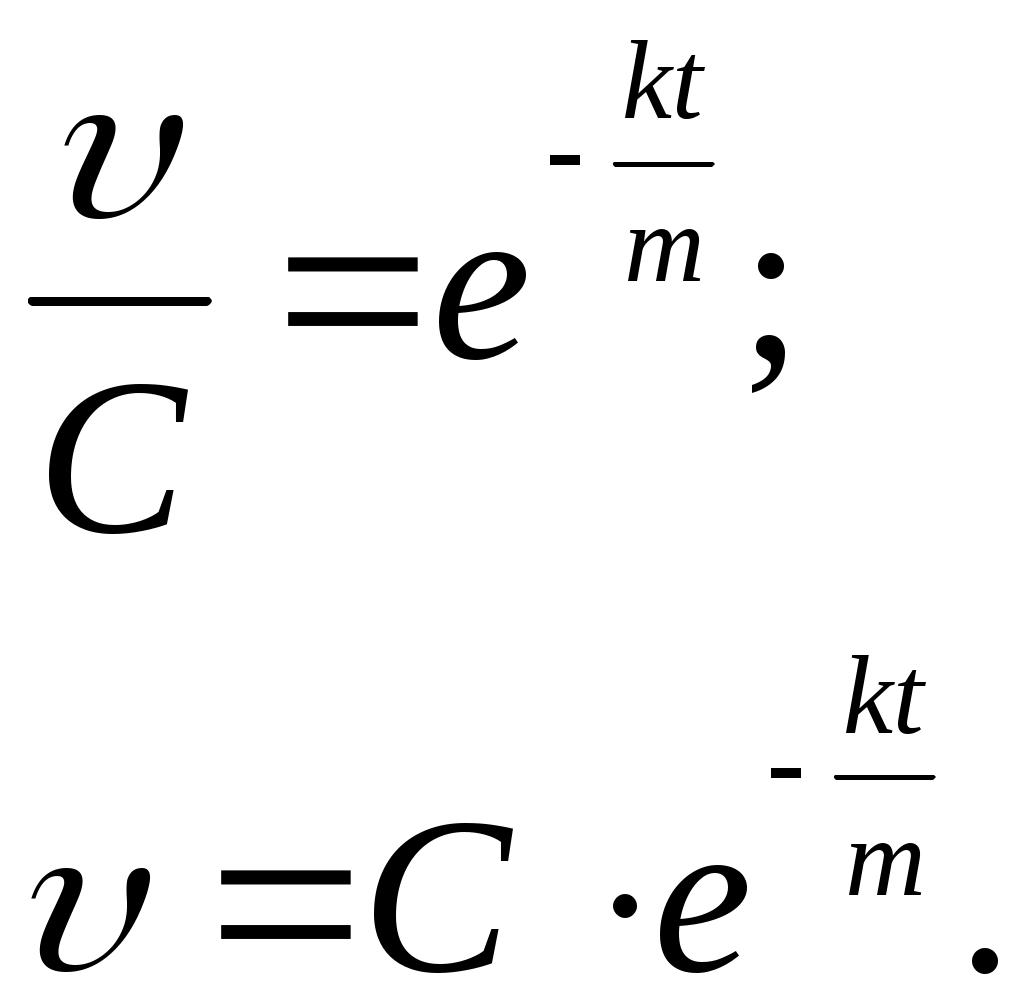



Найдём С, используя начальное условие 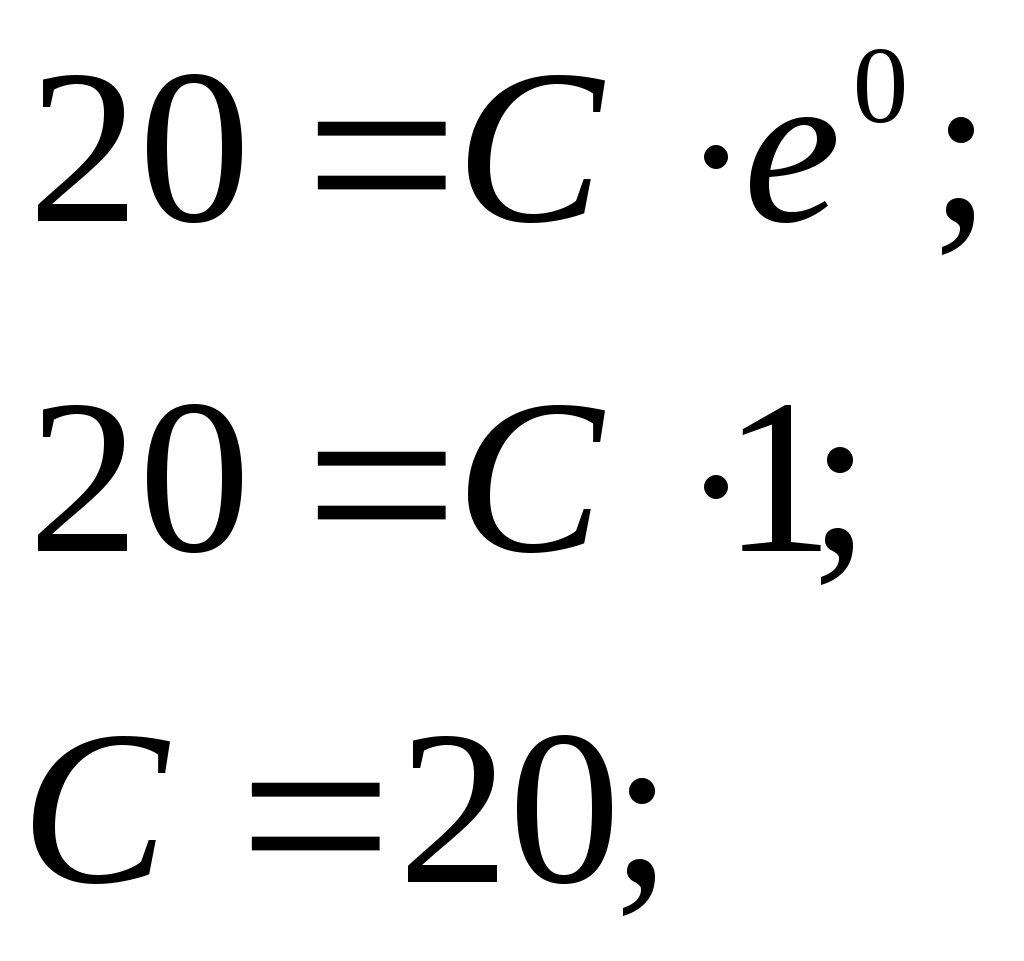при t = 0:



Поэтому .

Теперь, используя дополнительное условие – при t = 40c = - получаем или

Следовательно, .

Отсюда искомая скорость равна:



Задача 4. (Заряд конденсатора). Конденсатор ёмкостью С включается в цепь с напряжением U и сопротивлением R. Определить заряд конденсатора в момент времени t после включения.

Решение.
Сила I электрического тока представляет собой производную от количества электричества q, прошедшего через проводник, по времени t В момент t заряд конденсатора q и сила тока в цепи действует электродвижущая сила Е, равная разности между напряжением цепи U и напряжением конденсатора то есть

Согласно закону Ома

Поэтому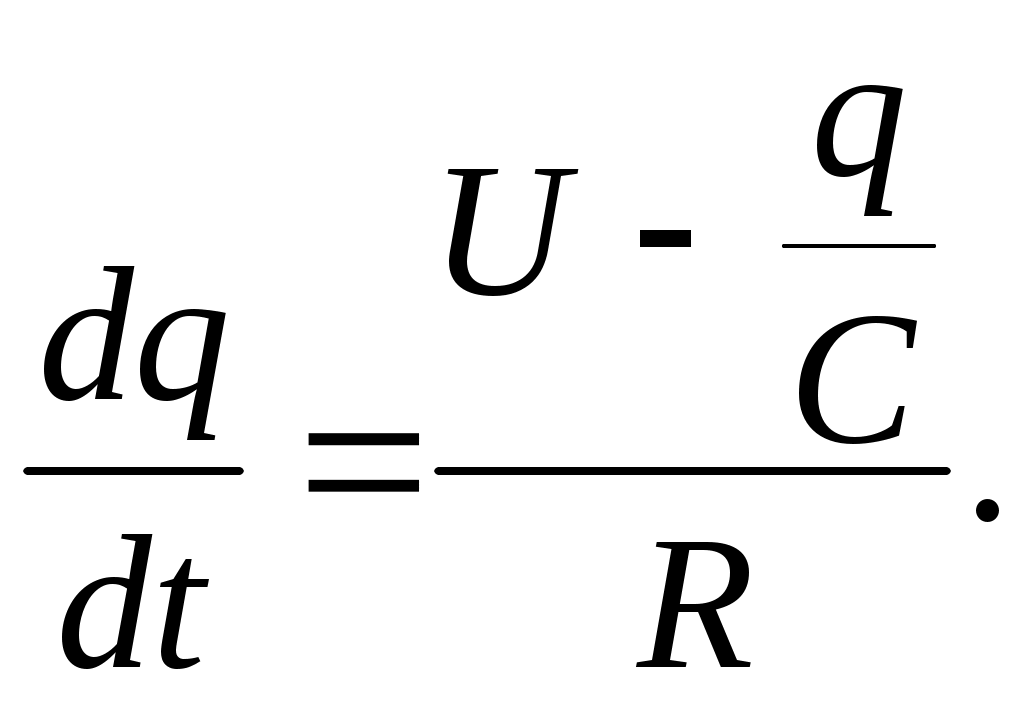

Отсюда

или ,

то есть, имеем дифференциальное уравнение с разделяющимися переменными.

Решим его: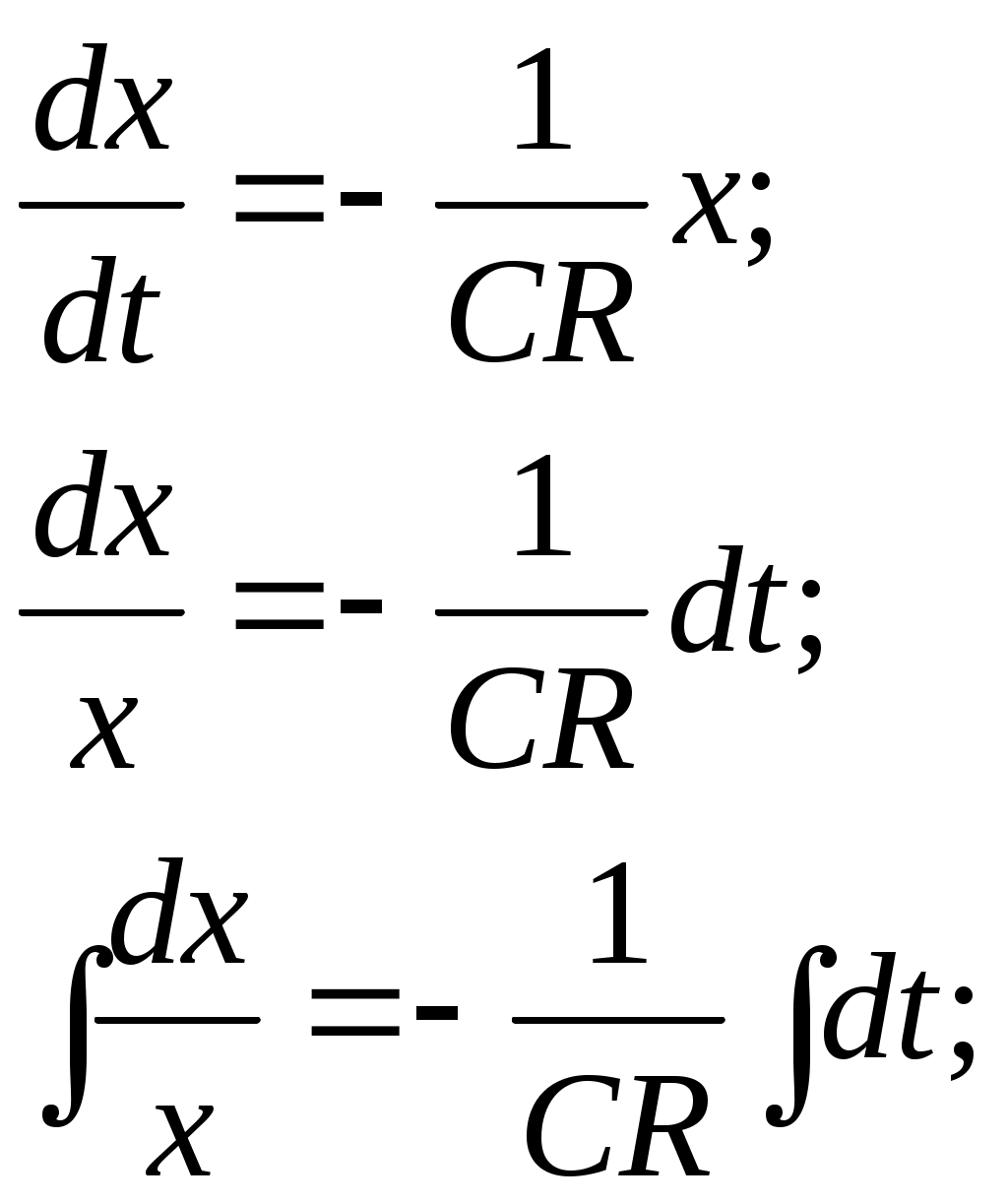







используя начальное условие x = СU при t=0, получим: или

Откуда

2. Линейные дифференциальные уравнения первого

порядка.

Задача №1.

Скорость v, путь s и время t связаны уравнением . Найти закон движения, если при t = 0 s = 2.
Решение:

Так как , то подставляя это значение v в данное уравнение, получаем дифференциальное уравнение движения:



или - это линейное дифференциальное уравнение первого порядка.

Решим его методом Бернулли, применив подстановку , где , ; , получаем

Сгруппировав члены, содержащие u и вынеся за скобки общий множитель, получим



Выражение в скобках приравняем к нулю: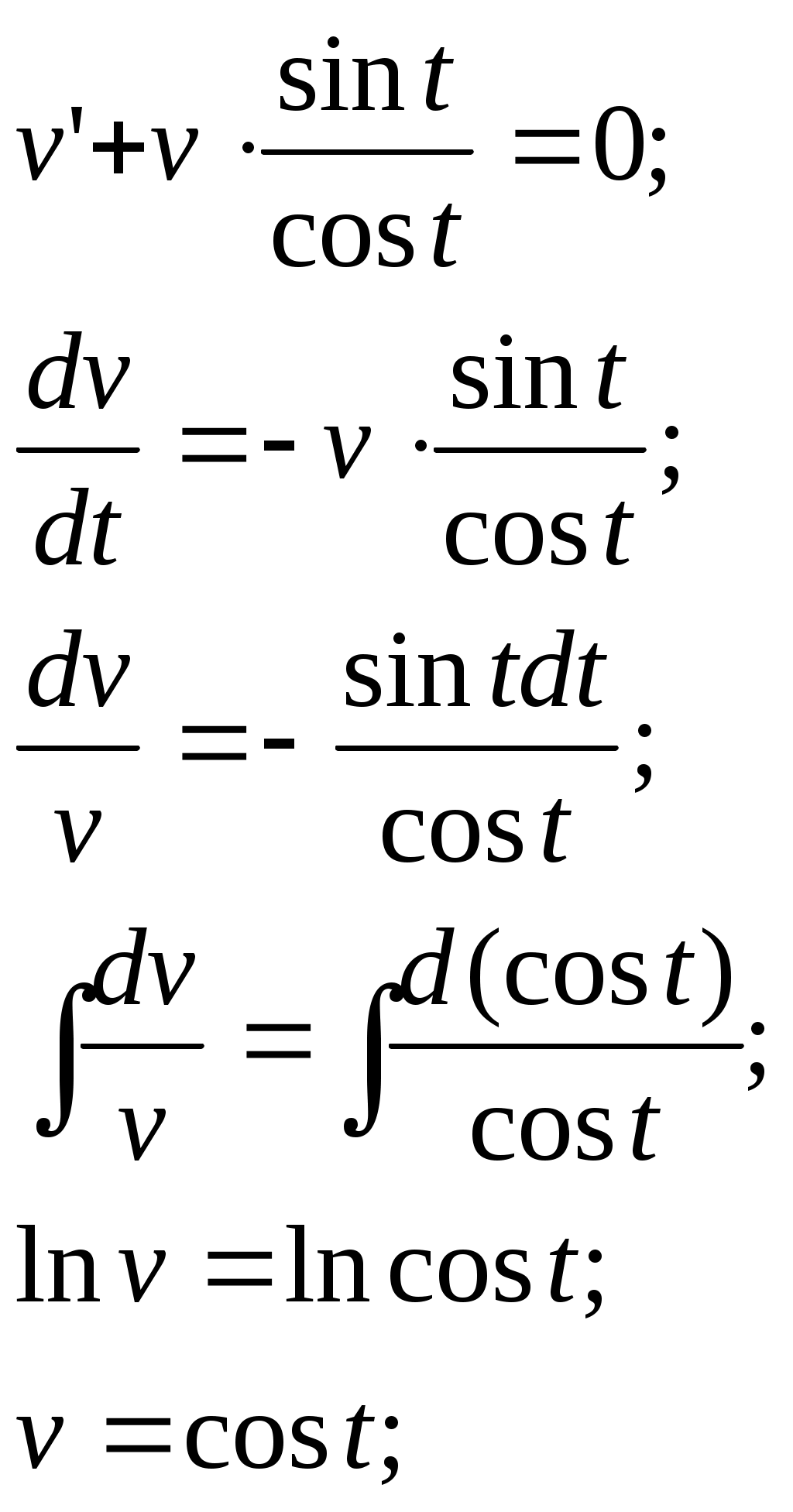



Для отыскания u имеем уравнение: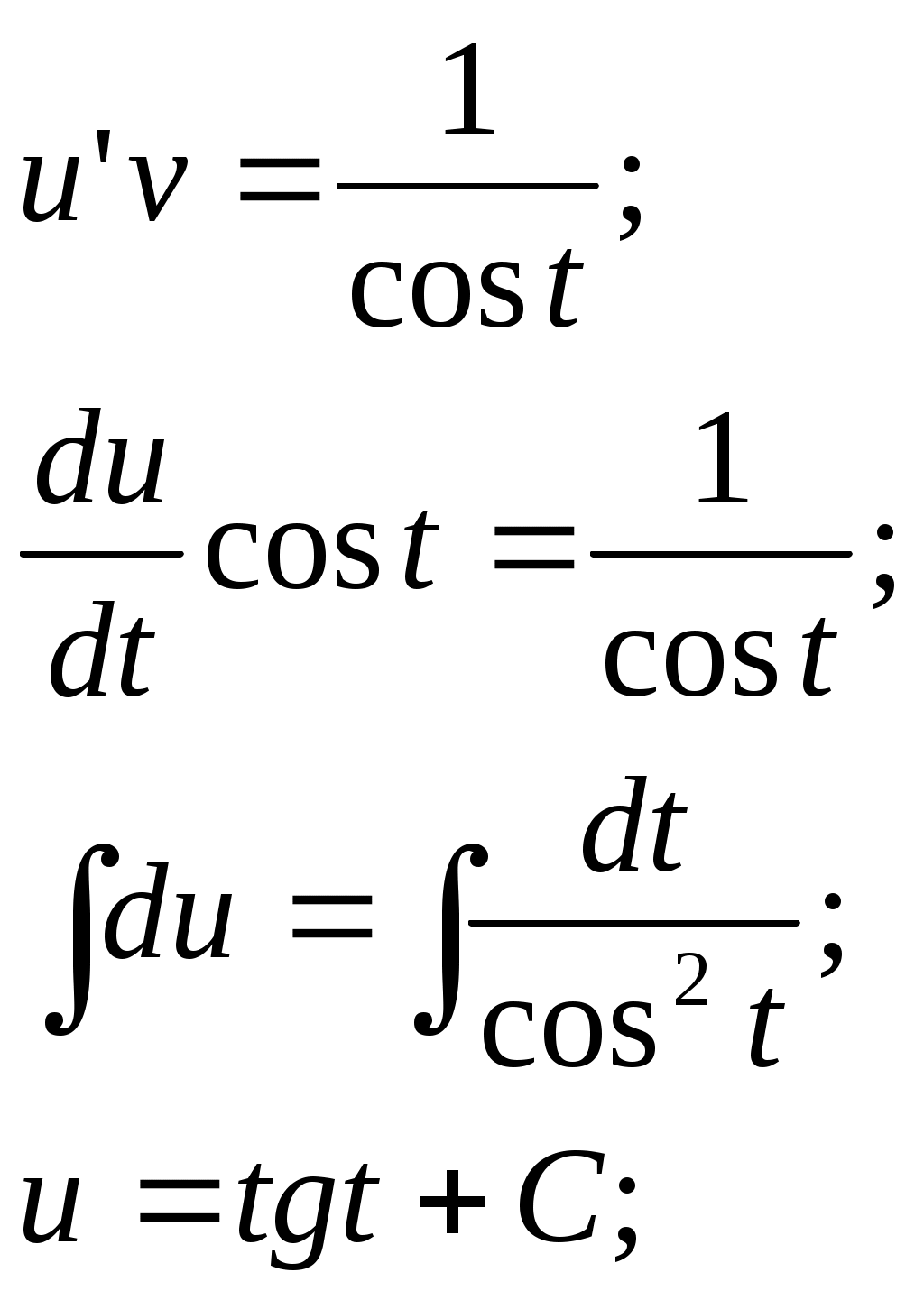





По условию при t=0 s=2 и поэтому С=2. Таким образом, искомый закон движения .
Задача2.

В помещении для крупного рогатого скота работают 2 вентилятора, каждый из которых в минуту доставляет по 60м³ чистого воздуха, содержащего 0,01% углекислоты. Полагая, что в коровнике объёмом 1600м³ с начальным содержанием углекислоты в 0,2% находится 120 коров, каждая из которых выдыхает в минуту 0,1м³ воздуха с 5% углекислоты, определить наличие углекислоты в 1м³ воздуха после двухчасового содержания животных в помещении.
Решение.

Пусть содержание углекислоты в 1м³ воздуха в момент времени t есть y(t) (в дальнейшем y). Скорость изменения концентрации равна приращению углекислоты у, делённому на соответствующий промежуток времени t; у определяется углекислотой:

1. 
   выделяемой при дыхании 120 животных,
   

2. 
   вводимой вентилятором на каждый кубометр,
   

3. 
   удаляемой за счёт работы вентиляторов
   

Следовательно,



Как видим, скорость изменения содержания углекислоты пропорциональна у. Перейдя к пределу при , имеем:

. Полу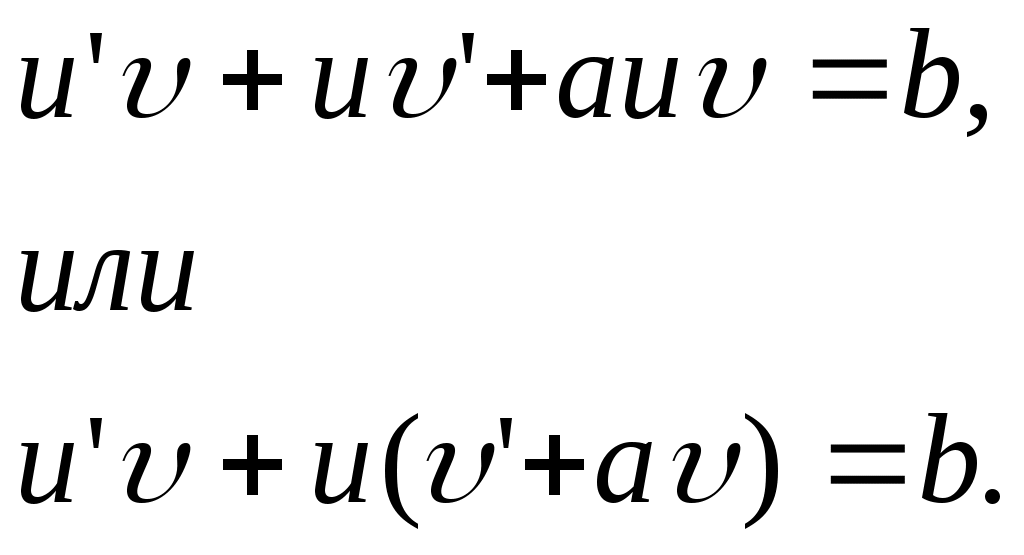чено линейное дифференциальное уравнение. Находим его решение. Имеем:

Обозначим тогда Примем следующее обозначение: и подставим в последнее уравнение. В результате получим:



Положим Тогда, учитывая, что , имеем





Определим произвольную постоянную С. При t = 0 согласно условию задачи у = 0,002.

Окончательно имеем:



Если t = 120, то у 0,00517, так как второй член очень мал



Таким образом, количество углекислоты в 1м³ (концентрация) увеличится в раза и в дальнейшем увеличиваться уже не будет благодаря работе вентиляторов.
3.Дифференциальные уравнения второго порядка.
Задача 1.

Тело движется прямолинейно с ускорением

Найти закон движения тела, если в начальный момент движения, пройденный путь и скорость равны нулю.
Решение.
Решая данное уравнение, как уравнение типа , получаем

Теперь, используя начальные условия s(0) = 0, , находим: С₂ = 0, С₁ = 0.

Следовательно,
Задача 2.

Материальная точка массой m движется по прямой линии к центру О, притягивающему её силой , где r – расстояние от точки до центра. Движение начинается с состояния покоя при r=a. Найти время, за которое точка достигает центра.


Решение.

По условию задачи в любой момент времени t на точку действует сила . (Иначе сила = масса ускорение). Ускорение равно . Получаем дифференциальное уравнение: или - дифференциальное уравнение второго порядка, не содержащее независимой переменной и производной первого порядка искомой функции.

Обозначим 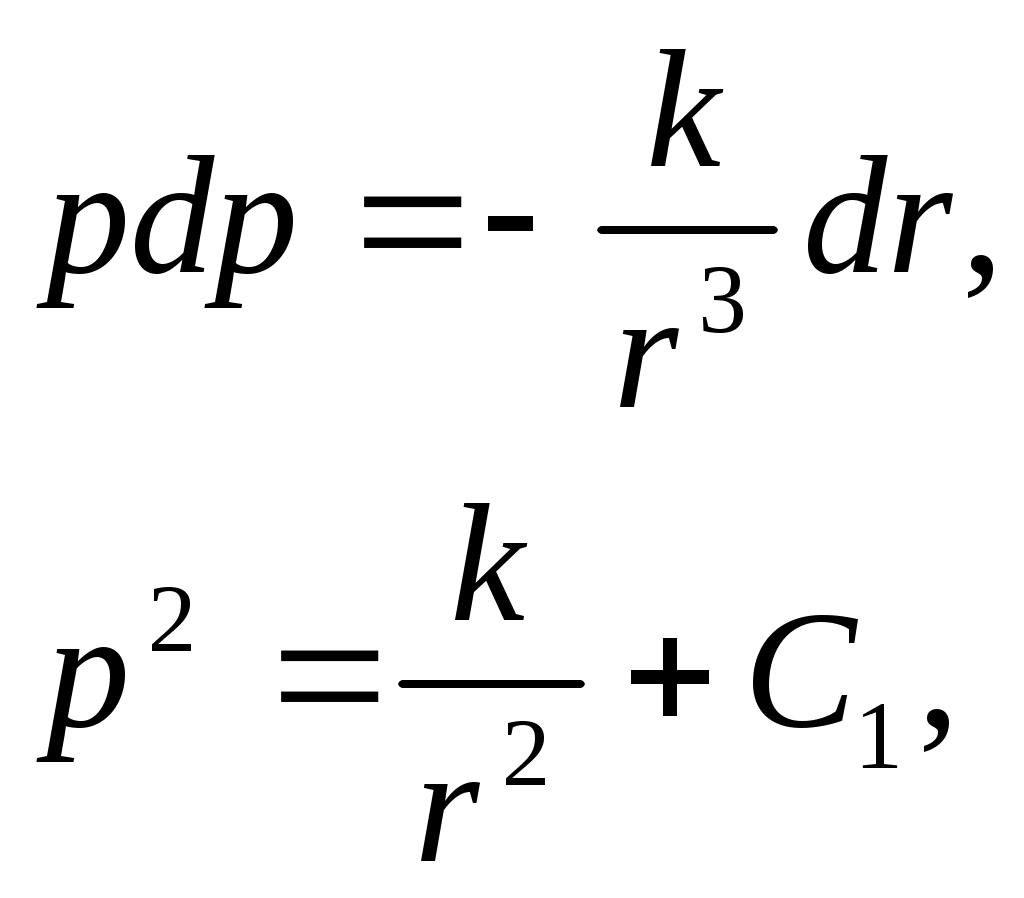. Тогда и последнее уравнение перепишем в виде дифференциальное уравнение с разделяющимися переменными. Разделяя переменные и интегрируя будем иметь:



Откуда (перед радикалом ставится знак минус, так как по смыслу задачи функция r убывает и ).

Или

Разделяя переменные в последнем уравнении и затем интегрируя, получаем: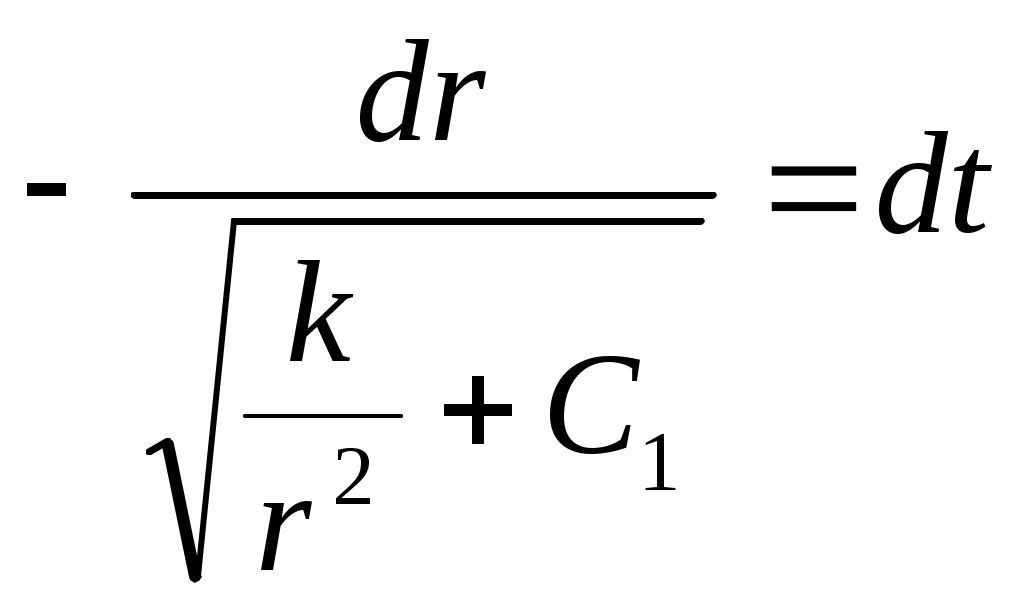

или

Используя начальные условия, имеем: при t = 0, r = a, .

Получим:

Откуда: .

Поэтому: .

Когда точка достигнет центра О, расстояние r = 0 и искомое время .