Тема урока. Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла
 Скачать 68.57 Kb. Скачать 68.57 Kb.
|
|
Тема урока: «Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла» Цель: рассмотреть типичные задачи, связанные с определенным интегралом, и его понятие. Сообщение темы и цели уроков Изучение нового материала Типичные задачи Задача 1. Площадь криволинейной трапеции. В курсе геометрии были получены формулы для вычисления площадей простейших фигур (треугольники и некоторые многоугольники) и объемов тел (призмы, пирамиды, цилиндры, конусы, шары). В то же время круг таких задач намного разнообразнее, и необходимо рассмотреть общий подход к подобным задачам. 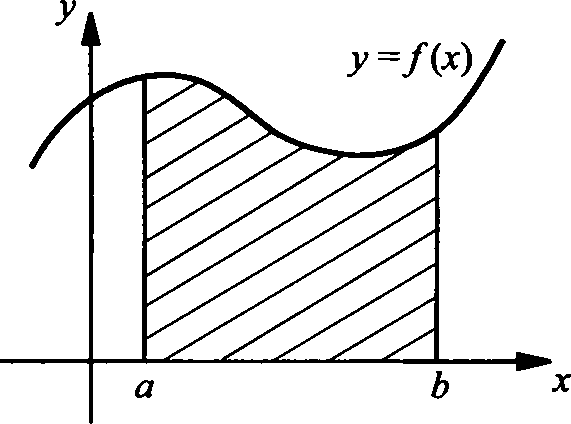 Сначала рассмотрим понятие криволинейной трапеции. Пусть на отрезке [a; b] оси абсцисс задана непрерывная функция f(x), не меняющая на нем знака. Фигуру, ограниченную графиком этой функцией, отрезком [а; b] ипрямыми Сначала рассмотрим понятие криволинейной трапеции. Пусть на отрезке [a; b] оси абсцисс задана непрерывная функция f(x), не меняющая на нем знака. Фигуру, ограниченную графиком этой функцией, отрезком [а; b] ипрямыми 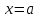 и и 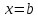 называют криволинейной трапецией. называют криволинейной трапецией.Было бы заманчиво научиться вычислять пощади криволинейных тралений в случае произвольных функций 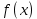 . .Разобьем отрезок [а; b]на n равных частей точками x1, x2, … xn. Построим прямоугольник со сторонами xk+1 –xk и f(xk). 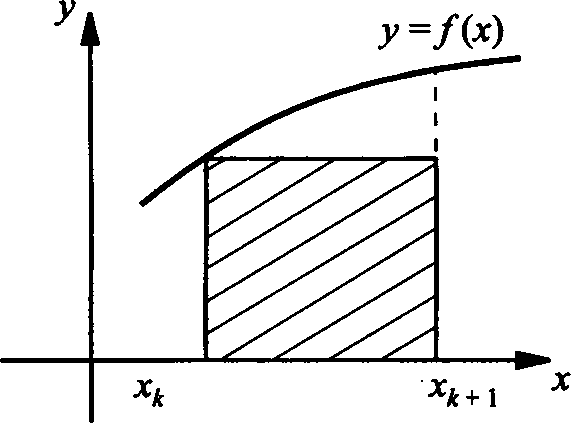 Площадь такого прямоугольника равна Площадь такого прямоугольника равна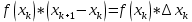 (где (где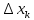 – длина отрезка [xk+1; xk], т.е. – длина отрезка [xk+1; xk], т.е.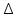 xk= xk+1 - xk). Если такую процедуру проделать для всех значений х (х = 0, 1, 2, ..., n — 1), то площадь криволинейной трапеции S можно приближенно оценить площадью ступенчатой фигуры. xk= xk+1 - xk). Если такую процедуру проделать для всех значений х (х = 0, 1, 2, ..., n — 1), то площадь криволинейной трапеции S можно приближенно оценить площадью ступенчатой фигуры.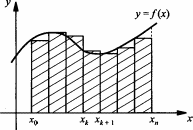 |
