дискретка. диск.математика. Задайте всеми известными способами соответствие между множествами
 Скачать 111.79 Kb. Скачать 111.79 Kb.
|
|
Задайте всеми известными способами соответствие между множествами  «число х является делителем числа у «число х является делителем числа упри помощи графа 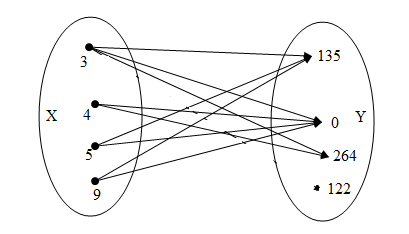 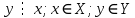 Перечислением пар элементов находящихся в данном соответствии  При помощи графика, так как между парами чисел принадлежащих подмножеству декартова произведения  и точками плоскости существует взаимно однозначное соответствие и точками плоскости существует взаимно однозначное соответствие При помощи таблицы
Пусть Х множество действительных чисел, У – множество точек координатной прямой. Соответствие между ними таково: действительному числу сопоставляется точка координатной прямой. Является ли это соответствие взаимно однозначным? Каждому действительному числу соответствует единственная точка на прямой и каждой точке на прямой соответствует единственное действительное число. Данное соответствие взаимно однозначно Выяснить какие из следующих отношений обладают свойством транзитивности, антиранзитивности, не обладает ни тем ни другим свойством R – быть больше в 3 раза на множестве N Транзитивность:  это ложь,данное отношение антитранзитивно это ложь,данное отношение антитранзитивноЖить на одном этаже на множестве людей Отношение транзитивно так как если один челове живет с други на одном этаже, а другой человек живет с третьим на одном этаже, значит первый с третьим также живут на одном этаже Иметь общую площадь на множестве множеств Данное отношение не обладает ни транзитивность ни антитранзитивностью так как иметь общую площадь могут только совпадающие элементы Среди графов укажите графы отношений  Рефлексивного и транзитивного а);б) Рефлексивного и симметричного а);в) Антисиметричного и транзитивного б) Рефлексивного, симметричного и транзитивного а) На множестве 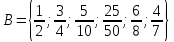 задано отношение « дробь х равна дроби у» Объясните, почему данное отношение является отношением эквивалентности, запишите классы эквивалентности задано отношение « дробь х равна дроби у» Объясните, почему данное отношение является отношением эквивалентности, запишите классы эквивалентностиОтношение В рефлексивно так как любая дробь равна себе самой, семметрично так как если дробь х равна броби у то и наобарот тоже верно, транзитивно так как если дробь х равна дроби у, а дробь у равна дроби z , значит дробь х равна дроби z. Значит о тношение В является отношением эквивалентности Выделим классы эквивалентности 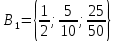 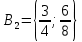  Графы отношений P, Q и M приведены на рисунке.  Определите свойства данных отношений. Определите свойства данных отношений и укажите среди них Отношение эквивалентности Порядка а) 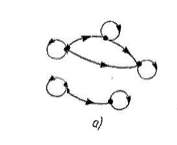 Отношение рефлексивно так как у каждой вершины есть петля ( верно 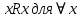 ) )Отношение не симметрично (стрелка от вершины к вершине идет только в одну сторону) Отношение транзитивно  Значит это отношение нестрогого порядка б)  Рефлексивно( у каждой вершины есть петля) Симметрично ( между кажой парой вершин существуют стрелки и в ту и в другую сторону) Транзитивно ( 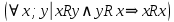 Это отношение эквивалентности в)  Отношение антирефлексивно Не симметрично Не транзитивно ( есть стрелка от 2 к 3 вершине и от 3 к 4, но нет дороги от 2 к 4) В начальном курсе математики на множестве натуральных чисел рассматривается отношения «меньше», «меньше на 5», «меньше в 3 раза», «непосредственно предшествует». Какие из них упорядочивают множество натуральных чисел Отношение «меньше» антирефлексивно, антисимметрично и транзитивно значит оно является отношением строгого порядка и значит оно упорядочивает множество N Отношение «меньше на 5» не транзитивно, например 8 меньше 13 на 5, а 3 меньше 8 на 5, но 3 меньше 13 на 10. Это не отношение порядка Аналагочно отношение «меньше в 3 раза» оно тоже не обладает свойством транзитивности и значит не является отношением порядка Отношение «непосредственно предшествует» тоже не транзитивно, например: 3 непосредственно предшествуе 4, а 2 непосредственно предшествует 3, но 2 не предшествствует непосредственно 4. Это тоже не является отношением порядка Являются сложение, умножение, вычитание и деление алгебраическими операциями на множестве М если:  На множестве М задана алгебраическая операция если каждой паре их множества элементов из множества М соответствует единственный элемент из этого множества. 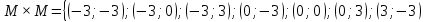 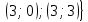 Умножение на множестве М  Алгебраическая операция умножения не задана на множестве М Сложение на множестве М 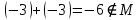 Алгебраическая операция сложения не задана на множестве М Вычитание на множестве М 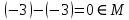   Алгебраическая операция вычитания не задана на множестве М Деление на множестве М 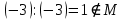 Алгебраическая операция деления не задана на множестве М б) множество нечетных натуральных чисел Умножение на множестве М При умножении любого нечетного натурального числа на нечетное натуральное число получается также нечетное натуральное число, значит алгебраическая операция умножения задана на множестве М Сложение на множестве М При сложении двух нечетных чисел получается четное число которое не принадлежит множеству М, а значит алгебраическая операция сложения не задана на множестве М Вычитание на множестве М При вычитании двух нечетных чисел получается четное число, а может получиться и отрицательное которое не является натуральным и не принадлежит множеству М. Алгебраическая операция вычитания не задана на множестве М Деление на множестве М При делении нечетных чисел может получиться дробное число которое не является натуральным а значит не принадлежит множеству М. Алгебраическая операция деления не задана на множестве М в) множество четных натуральных чисел Умножение на множестве М При умножении любого четного натурального числа на четное натуральное число получается также четное натуральное число, значит алгебраическая операция умножения задана на множестве М Сложение на множестве М При сложении двух четных чисел получается четное число которое принадлежит множеству М, а значит алгебраическая операция сложения задана на множестве М Вычитание на множестве М При вычитании двух четных чисел получается четное число, но может получиться и отрицательное которое не является натуральным и не принадлежит множеству М. Алгебраическая операция вычитания не задана на множестве М Деление на множестве М При делении четных чисел может получиться нечетное число которое не принадлежит множеству М. Алгебраическая операция деления не задана на множестве М Применяя дистрибутивный закон умножения относительно сложения и вычитания, найдите значение выражения Алгебраическая операция 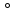 называется дистрибутивной относительно алгебраической операции *, если для называется дистрибутивной относительно алгебраической операции *, если для  выполняются равенства выполняются равенства  Опираясь на этот закон получим:  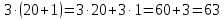  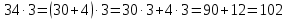 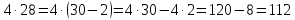 Найдите рациональное число, симметричное относительно умножения числу: Нейтральным элементом относительно операции умножения является 1 а)  симетричным относительно операции умножения для числа 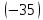 будет число будет число  б) 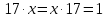 симетричным относительно операции умножения для числа  будет число будет число 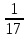 в) 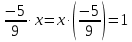 симетричным относительно операции умножения для числа 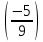 будет число будет число 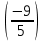 г)  симетричным относительно операции умножения для числа  будет число будет число  Образует ли группу множество: Всех целых чисел кратных 7 относительно сложения Множество состоит из элементов  и т.д. Результат сложения дает число кратное 7 . Множество образует группу и т.д. Результат сложения дает число кратное 7 . Множество образует группуВсех целых чисел вида 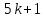 относительно умножения относительно умноженияМножество состоит из элементов вида  при умножении чисел множества получится число последней цифрой которого будет 6 или 1значит результат тоже будет принадлежать данному множеству. Данное множество образует группу. при умножении чисел множества получится число последней цифрой которого будет 6 или 1значит результат тоже будет принадлежать данному множеству. Данное множество образует группу.Пусть множество Х состоит из чисел 1,2,3,4,5 сумма чисел  определяется как остаток от деления определяется как остаток от деления  на 6, а их произведение как остаток от деления на 6, а их произведение как остаток от деления  на 6. Докажите, что Х является кольцом относительно этих операций и что в нем есть не нулевые элементы, произведение которых равно нулю на 6. Докажите, что Х является кольцом относительно этих операций и что в нем есть не нулевые элементы, произведение которых равно нулюОперация сложения коммутативна  Операция сложения ассоциативна   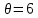  Для каждого элемента существует противоположный ему элемент 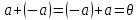 Операция умножения на множестве Х ассоциативна 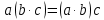 Данные операции связаны законами дистрибутивности Произведение чисел 2 и 3 дает 6 остаток от деления на 6 будет 0 Прочитайте записи  Приведите примеры множеств А и В удовлетворяющих этим условиям. Приведите примеры множеств А и В удовлетворяющих этим условиям. - множество А содержит 6 элементов - множество А содержит 6 элементов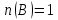 - множество В содержит 1 элемент - множество В содержит 1 элемент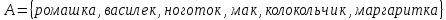 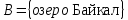 13.2 Придумайте множества C и D для которых выполняются условия а)    б)    Используя определение произведения целых неотрицательных чисел, покажите, что   Возьмем множесто А, содержащее 5 элементов Возьмем множесто А, содержащее 5 элементов 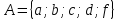 и множество В в котором два элемента, и множество В в котором два элемента, 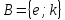 . Найдем декартово произведение множеств А и В . Найдем декартово произведение множеств А и В Оно содержит 10 элементов , значит   Возьмем множесто А, содержащее 1 элемент Возьмем множесто А, содержащее 1 элемент  и множество В в котором 7 элементов, и множество В в котором 7 элементов, 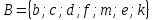 . Найдем декартово произведение множеств А и В . Найдем декартово произведение множеств А и В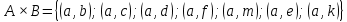 Оно содержит 7 элементов , значит  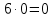 Возьмем множесто А, содержащее 6 элементов Возьмем множесто А, содержащее 6 элементов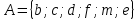 и множество В в котором нет элементов, и множество В в котором нет элементов, 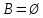 . Найдем декартово произведение множеств А и В . Найдем декартово произведение множеств А и В значит значит 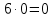 Используя определение частного целых неотрицательных чисел покажите, что  Возьмем множесто А, содержащее 12 элементов 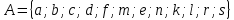 Разобьем множество А на 3 попарно Разобьем множество А на 3 попарнонепересекающихся равномощных подмножества 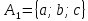  таких множеств 4, значит таких множеств 4, значит  Возьмем множесто А, содержащее 6 элементов  множество разбивается на 6 непересекающихся множеств множество разбивается на 6 непересекающихся множеств   , значит , значит  Дайте теоретическо-множественное обоснование выбора действий при решении задач Оля собрала грибы: 3 белых и 2 подосиновика. Сколько грибов собрала Оля Задача на одно действие  . У нас два множества в первом 3 элемента, во втором 2 Результирующее множество является объединением первых двух, значит число элементов находят сложением . У нас два множества в первом 3 элемента, во втором 2 Результирующее множество является объединением первых двух, значит число элементов находят сложением  У кати было 3 шара, а у Тани на 1 больше. Сколько шаров было у Тани В первом множестве 3 элемента, а во втором не знаем сколько но знаем , что на 1 больше. Значит присутствует множество содержащее 1 элемент. Искомое множество нахожим сложением то есть у Тани  шара шараНа станцию прибыло 7 вагонов с углем . Три вагона разгрузили . Сколько вагонов осталось разгрузить? Рассматриваем множество А в котором 7 элементов, затем из него выделена 2 подмножества причем в одном из них В- 3 элемента. Значит множество С – число не разгруженых вагонов является дополнение множества В до множества А. Значит число элементов множества С находят вычитанием 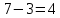 неразгруженных вагона неразгруженных вагонаВ зоопарке 6 медведей, а верблюдов на два меньше. Сколько верблюдов в зоопарке? Рассматриваем множество медведей А в котором 6 элементов, а множество В содержит на 2 элемента меньше , значит присутствует множество С содержащее 2 элемена которое является дополнением множества В до множества А . Значит множество В находим вычитанием 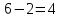 верблюдов верблюдовУченица прочита в первый день 9 страниц книги, а во второй в два раза больше, чем в первый. Сколько страниц книги прочитала ученица во второй день? В первом множестве А 9 элементов, а во вторм В не знаем сколько но в два раза больше, то есть оно является объединением двух множеств, каждое из которых содержит столькоже элементов сколько в множестве А, значит число элементов в множестве В находим умножением.  страниц книги прочитала ученица во второй день страниц книги прочитала ученица во второй деньДля уроков труда девочка принесла 6 листов красной бумаги, это в два раза меньше чем зеленой. Сколько листов зеленой бумаги принесла девочка? Значит, зеленой бумаги в двое больше то есть множество листов зеленой бумаги А является объединением двух множеств содедержащих по 6 элементов , значит множество А находим умножением  листов зеленой бумаги принесла девочка листов зеленой бумаги принесла девочка6 кусков сахара разложили в стаканы с чаем , по два куска в каждый. На сколько стаканов чая хватило сахара? Множество В содержащее 6 элементов разбивается на 2 равночисленных множества. Число элементов в каждом таком подмножестве находят делением  стакана чая стакана чаяУ Коли 12 кроликов, а у вовы в 4 раза меньше , чем у Коли. Сколько кроликов у Вовы Множество В содержащее 12 элементов разбивается на 4 равночисленных множества. Число элементов в каждом таком подмножестве находят делением  кролика у Вовы кролика у Вовы |
