Модуль 1 Мокрецов Олег Александрович. Задание 1 (2 балла)
 Скачать 4.42 Mb.
|
|
Модуль «Специфика предметного содержания» Модуль 1. Мокрецов Олег Александрович Задание 1 (2 балла) а) Решите уравнение 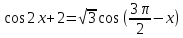 . б) Укажите корни этого уравнения, принадлежащие отрезку 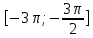 . Задание 2 (2 балла) Решите неравенство: 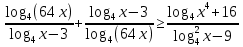 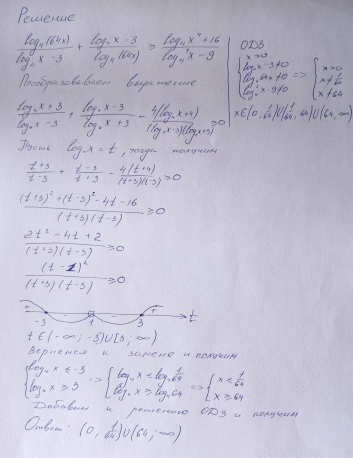 Задание 3 (2 балла) Лев взял кредит в банке на срок 40 месяцев. По договору Лев должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется p% этой суммы, затем следует платеж Льва. а) Ежемесячные платежи подбираются таким образом, чтобы долг уменьшался равномерно. б) Известно, что наибольший платеж Льва был в 25 раз меньше первоначальной суммы долга. Найдите p.  Задание 4 (3 балла) В правильной треугольной пирамиде SABC сторона AB равна 6, а боковое ребро SA равно 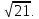 На ребрах AB и SB отмечены точки M и K соответственно, причем AM =4, SK : KB =1 : 3.а) Докажите, что плоскость CKM перпендикулярна плоскости АВС. б) Найдите объем пирамиды BCKM. 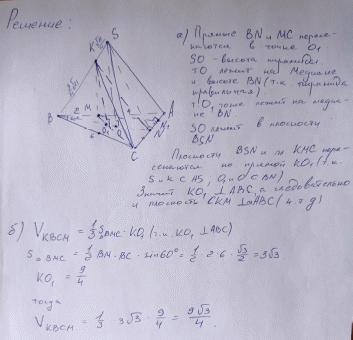 Задание 5 (3 балла) В прямоугольном треугольнике ABC точка М лежит на катете АС, а точка N лежит на продолжении катета ВС за точку С, причем СМ = ВС и CN = АС. а) Отрезки CP и CQ – медианы треугольников АВС и NCM соответственно. Докажите, что прямые CP и CQ перпендикулярны. б) Прямые MN и AB пересекаются в точке К, а прямые BM и AN – в точке L. Найдите KL, если ВС = 1, а АС = 5. 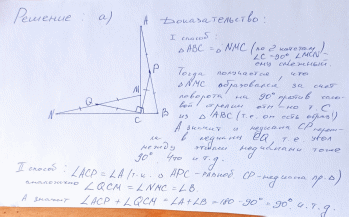  |