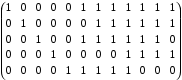|
Дискретка. Задание 1 Докажите тождества, используя только определения операций над множествами. 1 2 то невозможно будет определить кортеж, принадлежащий а значит, доказать соотношение становится невозможно. Задание 2

                
Задание 1:
Докажите тождества, используя только определения операций над множествами.
1) 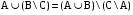
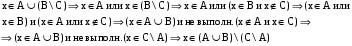 2) 2)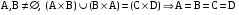 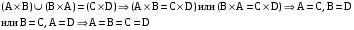 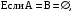 то невозможно будет определить кортеж, принадлежащий то невозможно будет определить кортеж, принадлежащий 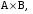 а значит, доказать соотношение становится невозможно. а значит, доказать соотношение становится невозможно.
Задание 2:
Докажите утверждение.
(0,1] [0, 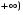
Для доказательства эквивалентности необходимо построить биекцию между этими интервалами. Этой биекцией будет функция:
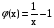
Так как между точками интервалов существует взаимно-однозначное соответствие, то (0,1]
[0,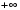 ). ).
Задание 3:
Докажите методом математической индукции, что 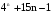 кратно 9 для всех кратно 9 для всех 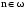 . .
Найдем базис индукции:
n=0
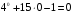 – кратно 9 – кратно 9
Предположим, что 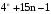 кратно 9 для некоторого n. кратно 9 для некоторого n.
Докажем, что 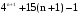 также кратно 9. также кратно 9.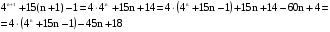
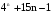 – кратно 9 по предположению индукции – кратно 9 по предположению индукции
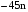 – кратно 9. – кратно 9.
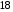 – кратно 9. – кратно 9.
Значит, так как справедливость утверждения доказана для n+1, то верно утверждение, что 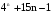 кратно 9 для всех кратно 9 для всех 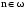 . .
Задание 4:
A={a,b,c}, B={1,2,3,4}, 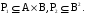 Изобразите Изобразите 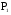 , , 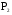 графически. Найдите [ графически. Найдите [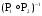 ]. Проверьте с помощью матрицы [ ]. Проверьте с помощью матрицы [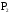 ], является ли отношение ], является ли отношение 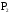 рефлексивным, симметричным, антисимметричным, транзитивным? рефлексивным, симметричным, антисимметричным, транзитивным?
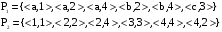
1
2
3
4
a
b
c
4
4
3
1
2
1
2
3
[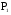 ]= ]=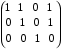 [ [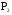 ]= ]=
[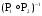 ]= ]=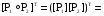 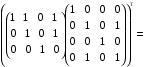 
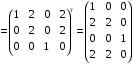
1) [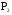 ]= ]= – по диагонали нет нулей – по диагонали нет нулей 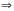 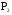 – рефлексивно. – рефлексивно.
2) 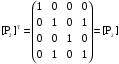 – поэтому – поэтому 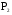 – симметрично. – симметрично.
3)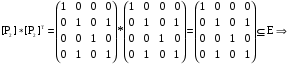 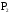 – неантисимметрично. – неантисимметрично.
4)
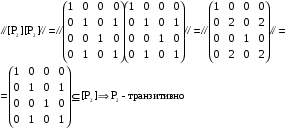 
Задание 5:
Найдите область определения, область значений отношения P. Является ли отношение P рефлексивным, симметричным, антисимметричным, транзитивным?
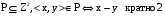
Область определения:
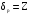
Область значений:
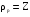
1) 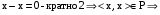 P – рефлексивно. P – рефлексивно.
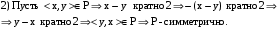
3) Так как 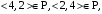 но но 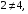 поэтому P – неантисимметрично. поэтому P – неантисимметрично.
4) 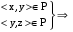 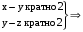 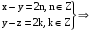 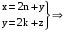
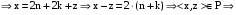 P – транзитивно. P – транзитивно.
Задание 6:
Является ли алгеброй следующий набор B=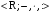 ? ?
Так как 0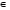 R, но при делении на ноль выходим за границы множества R, поэтому операция деления не замкнута на множестве R. Значит, набор B= R, но при делении на ноль выходим за границы множества R, поэтому операция деления не замкнута на множестве R. Значит, набор B=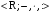 не является алгеброй. не является алгеброй.
Задание 7:
Постройте подсистему B(X), если B=<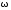 ;+, ;+,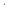 >, X={2} >, X={2}
Подставим элементы из X в термы из B.
2+2+2+…=2n, n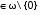
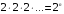 , n , n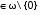
Получим, что B(X)=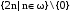 . .
Задание 8:
Используя многомодульную арифметику с вектором оснований 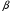 , вычислить , вычислить 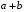 , , 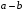 , , 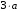 , , 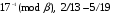 . Каков знак числа . Каков знак числа 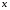 ? ?
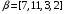 , , 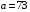 , , 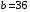 , , 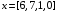
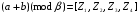
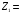 (73 (mod 7) + 36 (mod 7))(mod 7) = (3 + 1)(mod 7) = 4 (73 (mod 7) + 36 (mod 7))(mod 7) = (3 + 1)(mod 7) = 4
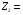 (73 (mod 11) + 36 (mod 11))(mod 11) = (7 + 3)(mod 11) = 10 (73 (mod 11) + 36 (mod 11))(mod 11) = (7 + 3)(mod 11) = 10
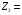 (73 (mod 3) + 36 (mod 3))(mod 3) = (1 + 0)(mod 3) = 1 (73 (mod 3) + 36 (mod 3))(mod 3) = (1 + 0)(mod 3) = 1
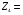 (73 (mod 2) + 36 (mod 2))(mod 2) = (1 + 0)(mod 2) = 1 (73 (mod 2) + 36 (mod 2))(mod 2) = (1 + 0)(mod 2) = 1
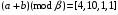
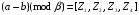
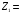 (73 (mod 7) – 36 (mod 7))(mod 7) = (3 – 1)(mod 7) = 2 (73 (mod 7) – 36 (mod 7))(mod 7) = (3 – 1)(mod 7) = 2
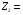 (73 (mod 11) – 36 (mod 11))(mod 11) = (7 – 3)(mod 11) = 4 (73 (mod 11) – 36 (mod 11))(mod 11) = (7 – 3)(mod 11) = 4
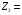 (73 (mod 3) – 36 (mod 3))(mod 3) = (1 – 0)(mod 3) = 1 (73 (mod 3) – 36 (mod 3))(mod 3) = (1 – 0)(mod 3) = 1
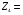 (73 (mod 2) – 36 (mod 2))(mod 2) = (1 – 0)(mod 2) = 1 (73 (mod 2) – 36 (mod 2))(mod 2) = (1 – 0)(mod 2) = 1
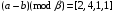
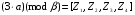
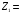 ( (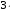 73) (mod 7) = 2 73) (mod 7) = 2
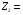 ( (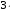 73) (mod 11) = 10 73) (mod 11) = 10
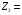 ( (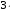 73) (mod 3) = 0 73) (mod 3) = 0
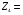 ( (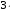 73) (mod 2) = 1 73) (mod 2) = 1
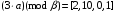
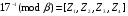
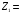 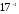 (mod 7) = 5 (mod 7) = 5 (mod 7) = 5 (mod 7) = 5
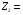 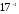 (mod 11) = 2 (mod 11) = 2 (mod 11) = 2 (mod 11) = 2
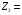 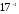 (mod 3) = 2 (mod 3) = 2 (mod 3) = 2 (mod 3) = 2
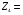 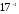 (mod 2) = 1 (mod 2) = 1 (mod 2) = 1 (mod 2) = 1
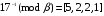
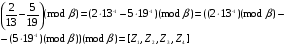
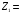 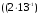 (mod 7) (mod 7) 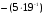 (mod 7))(mod 7) = (( (mod 7))(mod 7) = ((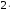 6)(mod 7) – 6)(mod 7) –
– 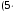 3)(mod 7))(mod 7) = (5 – 1)(mod 7) = 4 3)(mod 7))(mod 7) = (5 – 1)(mod 7) = 4
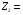 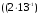 (mod 11) (mod 11) 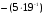 (mod 11))(mod 11) = (( (mod 11))(mod 11) = ((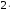 6)(mod 11) – 6)(mod 11) –
– 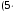 7)(mod 11))(mod 11) = (1 – 2)(mod 11) = 10 7)(mod 11))(mod 11) = (1 – 2)(mod 11) = 10
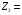 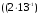 (mod 3) (mod 3) 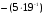 (mod 3))(mod 3) = (( (mod 3))(mod 3) = ((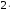 1)(mod 3) – 1)(mod 3) –
– 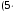 1)(mod 3))(mod 3) = (2 – 2)(mod 3) = 0 1)(mod 3))(mod 3) = (2 – 2)(mod 3) = 0
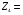 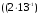 (mod 2) (mod 2) 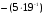 (mod 2))(mod 2) = (( (mod 2))(mod 2) = ((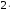 1)(mod 2) – 1)(mod 2) –
– 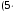 1)(mod 2))(mod 2) = (0 – 1)(mod 2) = 1 1)(mod 2))(mod 2) = (0 – 1)(mod 2) = 1
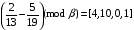
Определим знак числа 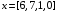
Очевидно, что 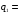 6 6
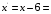 [0, 1, 1, 0] или [0, 1, 1, 0] или 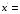 [1, 1, 0] [1, 1, 0]
Вектор оснований сокращаем до 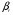 = [11, 3, 2] = [11, 3, 2]
Для вычисления 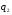 вычислим вычислим
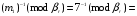 [8, 1, 1] [8, 1, 1]
Умножим 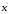 на этот элемент, в результате получим [8, 1, 0] на этот элемент, в результате получим [8, 1, 0]
Таким образом, 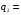 8 8
Вычитая 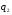 из последнего выражения, получаем из последнего выражения, получаем 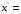 [0, 2, 0] или [0, 2, 0] или 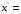 [2, 0] [2, 0]
Вектор оснований 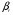 = [3, 2] = [3, 2]
Вычисляем 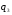
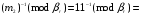 [2, 1] [2, 1]
Умножаем 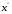 на полученный элемент, в результате получаем [4, 0] на полученный элемент, в результате получаем [4, 0]
Поэтому 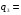 4 4
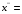 [0, 0] или [0, 0] или 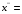 [0] для вектора оснований [0] для вектора оснований 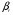 = [2] = [2]
Находим 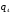
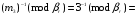 [1] [1]
При умножении на 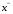 получаем [0] получаем [0]
Отсюда следует, что 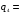 0 0
Поэтому число x – положительное.
Задание 9:
Даны графы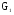 и и 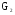 . Найдите . Найдите 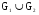 , , 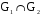 , , 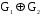 , , 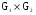 . Для графа . Для графа 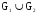 найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1. найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.
3
2
1
4
3
2
1

(4,3)
(3,3)
(2,3)
(1,3)
(4,2)
(3,2)
(2,2)
(1,2)
(1,1)
(2,1)
(3,1)
(4,1)
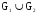
3
2
1
4
3
2
1
4
3
2
1
Рассмотрим граф  : :
Матрица смежности A=
4
1
3
2

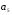
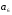
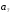
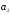
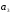
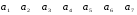
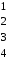 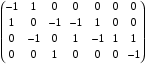 – матрица инцидентности – матрица инцидентности
B=E+A+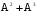 = = 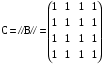
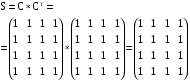 – матрица сильных компонент. – матрица сильных компонент.
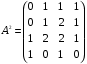 – матрица маршрутов длины 2. – матрица маршрутов длины 2.
Маршруты длины 2, исходящие из вершины 1:
(1;3;2), (1;3;3), (1;3;4).
Задание 10:
Найдите матрицы фундаментальных циклов, фундаментальных разрезов, радиус и диаметр, минимальное множество покрывающих цепей графа G. Является ли изображенный граф эйлеровым? Является ли изображенный граф планарным?
3
4
2
1
5
6
7
8
Получим остов графа. Для этого удалим из графа 12–8+1=5 ребер.
1
1
2
4
5
6
7
8
2
3
4
5
6
7
8
9
10
11
12
3
Матрица фундаментальных циклов:
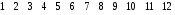
 C= C= 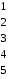 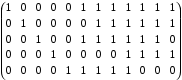
Матрица фундаментальных разрезов:
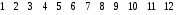
K= 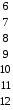 
Диаметр d(G)=3
Радиус r(G)=2
Минимальное множество покрывающих цепей графа – 2.
3,2,1,5,3,4,6,5,4,8,1
6,7,8
Граф не является эйлеровым, так как степени не всех его вершин четные.
Граф планарный.
1
3
2
4
5
6
7
8 |
|
|
 Скачать 241.68 Kb.
Скачать 241.68 Kb.

















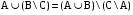
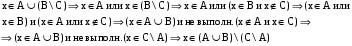 2)
2)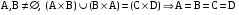
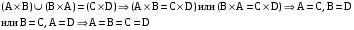
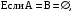 то невозможно будет определить кортеж, принадлежащий
то невозможно будет определить кортеж, принадлежащий 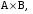 а значит, доказать соотношение становится невозможно.
а значит, доказать соотношение становится невозможно. 
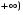
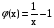
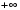 ).
).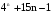 кратно 9 для всех
кратно 9 для всех 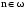 .
.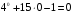 – кратно 9
– кратно 9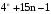 кратно 9 для некоторого n.
кратно 9 для некоторого n.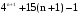 также кратно 9.
также кратно 9.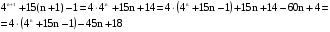
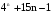 – кратно 9 по предположению индукции
– кратно 9 по предположению индукции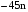 – кратно 9.
– кратно 9.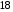 – кратно 9.
– кратно 9.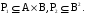 Изобразите
Изобразите 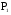 ,
, 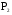 графически. Найдите [
графически. Найдите [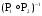 ]. Проверьте с помощью матрицы [
]. Проверьте с помощью матрицы [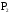 ], является ли отношение
], является ли отношение 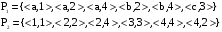
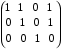 [
[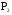 ]=
]=
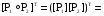
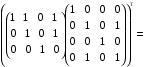

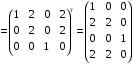
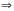
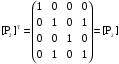 – поэтому
– поэтому 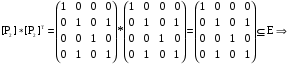
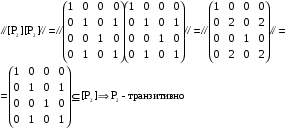
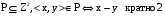
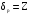
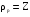
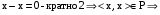 P – рефлексивно.
P – рефлексивно.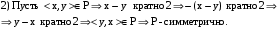
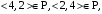 но
но 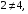 поэтому P – неантисимметрично.
поэтому P – неантисимметрично.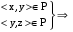
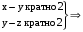
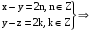
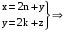
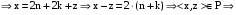 P – транзитивно.
P – транзитивно.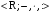 ?
?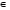 R, но при делении на ноль выходим за границы множества R, поэтому операция деления не замкнута на множестве R. Значит, набор B=
R, но при делении на ноль выходим за границы множества R, поэтому операция деления не замкнута на множестве R. Значит, набор B=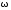 ;+,
;+,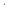 >, X={2}
>, X={2}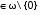
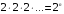 , n
, n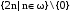 .
.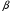 , вычислить
, вычислить 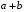 ,
, 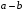 ,
, 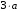 ,
, 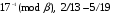 . Каков знак числа
. Каков знак числа 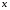 ?
?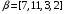 ,
, 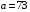 ,
, 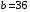 ,
, 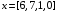
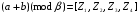
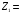 (73 (mod 7) + 36 (mod 7))(mod 7) = (3 + 1)(mod 7) = 4
(73 (mod 7) + 36 (mod 7))(mod 7) = (3 + 1)(mod 7) = 4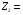 (73 (mod 11) + 36 (mod 11))(mod 11) = (7 + 3)(mod 11) = 10
(73 (mod 11) + 36 (mod 11))(mod 11) = (7 + 3)(mod 11) = 10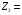 (73 (mod 3) + 36 (mod 3))(mod 3) = (1 + 0)(mod 3) = 1
(73 (mod 3) + 36 (mod 3))(mod 3) = (1 + 0)(mod 3) = 1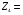 (73 (mod 2) + 36 (mod 2))(mod 2) = (1 + 0)(mod 2) = 1
(73 (mod 2) + 36 (mod 2))(mod 2) = (1 + 0)(mod 2) = 1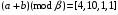
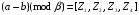
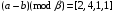
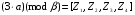
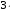 73) (mod 7) = 2
73) (mod 7) = 2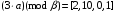
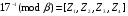
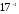 (mod 7) = 5 (mod 7) = 5
(mod 7) = 5 (mod 7) = 5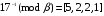
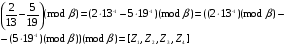
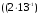 (mod 7)
(mod 7) 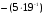 (mod 7))(mod 7) = ((
(mod 7))(mod 7) = ((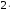 6)(mod 7) –
6)(mod 7) – 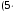 3)(mod 7))(mod 7) = (5 – 1)(mod 7) = 4
3)(mod 7))(mod 7) = (5 – 1)(mod 7) = 4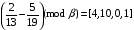
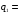 6
6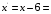 [0, 1, 1, 0] или
[0, 1, 1, 0] или 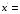 [1, 1, 0]
[1, 1, 0]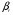 = [11, 3, 2]
= [11, 3, 2]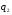 вычислим
вычислим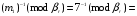 [8, 1, 1]
[8, 1, 1]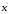 на этот элемент, в результате получим [8, 1, 0]
на этот элемент, в результате получим [8, 1, 0]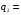 8
8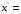 [0, 2, 0] или
[0, 2, 0] или 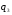
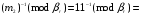 [2, 1]
[2, 1]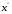 на полученный элемент, в результате получаем [4, 0]
на полученный элемент, в результате получаем [4, 0]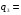 4
4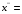 [0, 0] или
[0, 0] или 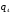
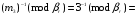 [1]
[1]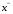 получаем [0]
получаем [0]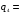 0
0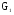 и
и 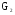 . Найдите
. Найдите 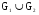 ,
, 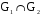 ,
, 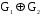 ,
, 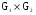 . Для графа
. Для графа 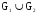 найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.
найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.


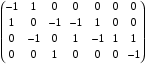 – матрица инцидентности
– матрица инцидентности 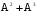 =
=
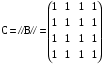
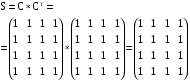 – матрица сильных компонент.
– матрица сильных компонент.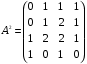 – матрица маршрутов длины 2.
– матрица маршрутов длины 2.