математика. Контрольная работа № 1. Задание 1 Определить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. Решение
 Скачать 89.95 Kb.
|
|
Задание 1 Определить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. 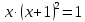 Решение Сначала нужно отделить решения. Удобно записать уравнение в виде 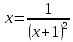 и построить графики двух элементарных функций 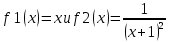 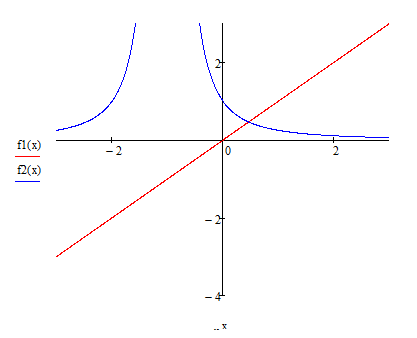 Из графика следует, что корень один: x * ∈ [0;1]. Представим уравнение в форме: x = x - λ(x*(x+1)2-1) Найдем максимальное значение производной от функции f(x) = x*(x+1)2-1 max(x•(2•x+2)+(x+1)2) ≈ 8 Значение λ = 1/(8) ≈ 0.125 Таким образом, решаем следующее уравнение: x-0.125*(x*(x+1)2-1) = 0 F(0)=-1; F(1)=3 Поскольку F(0)*F(1)<0 (т.е. значения функции на его концах имеют противоположные знаки), то корень лежит в пределах [0;1]. Остальные расчеты сведем в таблицу.
Ответ: x = 0.46359395923842; F(x) = -0.00693 Сходимость:  Задание 2 Отделить корни уравнения графически и уточнить один из них методом касательных с точностью до 0,001 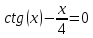 Решение Сначала нужно отделить решения. Удобно записать уравнение в виде 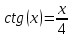 и построить графики двух элементарных функций 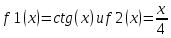 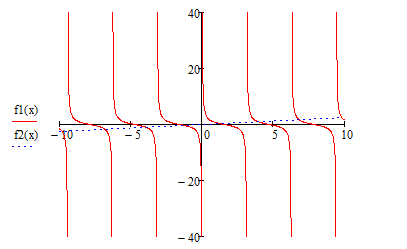 Из графика следует, что корень множество, возьмем: x * ∈ [0;1]. Сначала нужно выбрать начальное приближение. 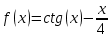 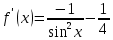 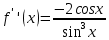 Вычислим несколько приближений: 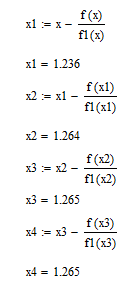 Решение получено за 4 итерации, так как поправка стала меньше заданной точности: 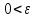 Задание 3 Методом итераций решить систему линейныx уравнений с точностью до 0,001. 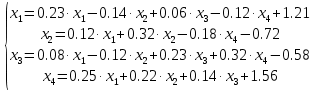 Решение Приведем к виду: x1=-5.261 - (-0.61x2+0.26x3-0.52x4) x2=2.25 - (0.38x1-0.56x4) x3=2.522 - (0.35x1-0.52x2+1.39x4) На главной диагонали матрицы присутствует нулевой элемент. Его необходимо исключить. Вычисления заканчиваются по критерию:  где  a = 0.348+0.522+1.391 = 2.2609  Поскольку 2.2609>1, то скорость итерационного процесса будет низкой. Необходимо сделать так, чтобы a → 0. Руководствуясь этим соображением, целесообразно сделать диагональное преобладание возможно более значительным (например, умножить какую-нибудь строку на коэффициент и прибавить к другой). Покажем вычисления на примере нескольких итераций. N=1 x1=-5.261 - 0*(-0.609) - 0*0.261 - 0*(-0.522)=-5.261 x2=2.25 - 0*0.375 - 0*0 - 0*(-0.563)=2.25 x3=2.522 - 0*0.348 - 0*(-0.522) - 0*1.391=2.522 x4=-1.56 - 0*0.25 - 0*0.22 - 0*0.14=-1.56 N=2 x1=-5.261 - 2.25*(-0.609) - 2.522*0.261 - (-1.56)*(-0.522)=-5.363 x2=2.25 - (-5.261)*0.375 - 2.522*0 - (-1.56)*(-0.563)=3.345 x3=2.522 - (-5.261)*0.348 - 2.25*(-0.522) - (-1.56)*1.391=7.696 x4=-1.56 - (-5.261)*0.25 - 2.25*0.22 - 2.522*0.14=-1.093 N=3 x1=-5.261 - 3.345*(-0.609) - 7.696*0.261 - (-1.093)*(-0.522)=-5.802 x2=2.25 - (-5.363)*0.375 - 7.696*0 - (-1.093)*(-0.563)=3.646 x3=2.522 - (-5.363)*0.348 - 3.345*(-0.522) - (-1.093)*1.391=7.653 x4=-1.56 - (-5.363)*0.25 - 3.345*0.22 - 7.696*0.14=-2.033 Остальные расчеты сведем в таблицу.
Для оценки погрешности вычисляем коэффициент α:  max[|x20,x21|] = ρ(x20, x21) = |-2.029 - (-2.028)| = 0.000908 Вычисляем погрешность:  Задание 4 Методом Гаусса-Зейделя решить с точностью 0,001 систему линейных уравнений, приведя ее к виду, удобному для итераций. 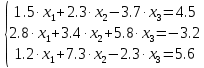 Решение Приведем к виду: x1=-1.143 - (1.21x2+2.07x3) x2=0.767 - (0.16x1-0.32x3) x3=-1.216 - (-0.41x1-0.62x2) Покажем вычисления на примере нескольких итераций. N=1 x1=-1.143 - 0*1.214 - 0*2.071=-1.143 x2=0.767 - (-1.143)*0.164 - 0*(-0.315)=0.955 x3=-1.216 - (-1.143)*(-0.405) - 0.955*(-0.622)=-1.086 N=2 x1=-1.143 - 0.955*1.214 - (-1.086)*2.071=-0.0531 x2=0.767 - (-0.0531)*0.164 - (-1.086)*(-0.315)=0.434 x3=-1.216 - (-0.0531)*(-0.405) - 0.434*(-0.622)=-0.968 N=3 x1=-1.143 - 0.434*1.214 - (-0.968)*2.071=0.336 x2=0.767 - 0.336*0.164 - (-0.968)*(-0.315)=0.407 x3=-1.216 - 0.336*(-0.405) - 0.407*(-0.622)=-0.827 Остальные расчеты сведем в таблицу.
Для оценки погрешности вычисляем коэффициент α:  max[|x9,x10|] = ρ(x9, x10) = |-0.88 - (-0.88)| = 0.000131 Вычисляем погрешность:  |