Стат радиотехника и радиоавтоматика. Задания 10.53, 12.53. Задание 10. 53 На вход радиотехнического устройства, состоящего из последовательно соединенных дифференцирующих устройств и сумматора (рис.
 Скачать 141.48 Kb. Скачать 141.48 Kb.
|
|
Задание 10.53 На вход радиотехнического устройства, состоящего из последовательно соединенных дифференцирующих устройств и сумматора (рис. 1), воздействует стационарный случайный процесс 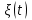 с нулевым математическим ожиданием с нулевым математическим ожиданием 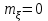 и корреляционной функцией и корреляционной функцией 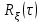 . .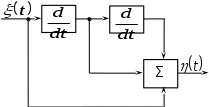 Рис. 1 – Последовательное соединение дифференцирующих устройств и сумматора Определить корреляционную функцию 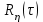 процесса процесса 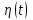 на выходе сумматора. на выходе сумматора.Решение Рассмотрим систему, описываемую линейным дифференциальным уравнением с постоянными или зависящими от времени коэффициентами: 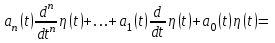 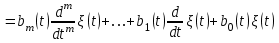 . (1) . (1)Здесь 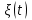 ‑ процесс на входе системы, характеризуемый математическим ожиданием ‑ процесс на входе системы, характеризуемый математическим ожиданием 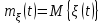 и корреляционной функцией: и корреляционной функцией: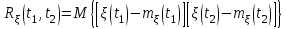 . .Вводя оператор 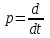 и операторы и операторы 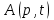 и и 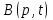 , определяемые равенствами: , определяемые равенствами: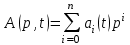 и и 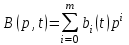 , (2) , (2)дифференциальное уравнение (1) можно привести к следующему операторному соотношению: 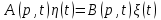 . (3) . (3)Из (3) формально следует равенство, определяющее сигнал на выходе системы в явном виде: 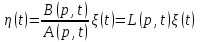 . (4) . (4)Оператор 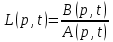 (5) (5)называется линейным однородным оператором системы. Динамическая система с оператором (5) линейна, так как при решении дифференциального уравнения (1) применим принцип суперпозиции. Линейным неоднородным оператором 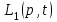 называется сумма линейного однородного оператора и некоторой заданной функции называется сумма линейного однородного оператора и некоторой заданной функции 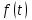 : :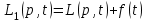 . (6) . (6)Путем вычитания из (6) функции 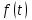 любой неоднородный оператор может быть приведен к однородному. Из (4) можно получить следующие соотношения, определяющие математические ожидания и корреляционные функции процессов на выходе линейных систем через их операторы и статистические характеристики входных процессов: любой неоднородный оператор может быть приведен к однородному. Из (4) можно получить следующие соотношения, определяющие математические ожидания и корреляционные функции процессов на выходе линейных систем через их операторы и статистические характеристики входных процессов: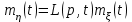 , (7) , (7)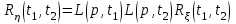 . (8) . (8)Как видно из рис. 2, случайный процесс 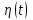 на выходе сумматора связан с воздействием на выходе сумматора связан с воздействием 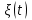 следующим образом: следующим образом: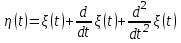 . (9) . (9)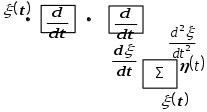 Рис. 2 – Последовательное соединение дифференцирующих устройств и сумматора Применяя формулу (8), имеем: 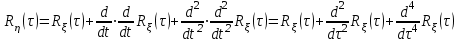 . .Задание 12.53 На рис. 1 приведена упрощенная схема двухканального коррелятора. На один из его входов поступает колебание 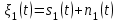 , ,а на другой 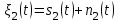 , ,Здесь 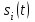 ‑ гармонические колебания частоты ‑ гармонические колебания частоты 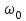 с различными амплитудами и начальными фазами: с различными амплитудами и начальными фазами: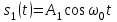 , , 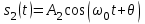 ; ;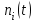 ‑ квазигармонические флуктуации: ‑ квазигармонические флуктуации: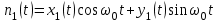 , ,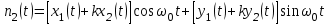 . . Рис. 1 – Двухканальный коррелятор с фильтром нижних частот Квадратурные составляющие 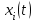 и и 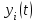 являются независимыми стационарными случайными процессами с нулевыми математическими ожиданиями и дисперсиями являются независимыми стационарными случайными процессами с нулевыми математическими ожиданиями и дисперсиями 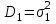 для для 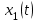 , , 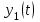 и и 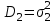 для для 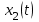 , , 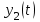 . Коэффициент . Коэффициент 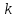 определяет степень коррелированности флуктуации определяет степень коррелированности флуктуации 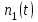 и и 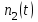 : :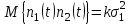 . .Определить математическое ожидание 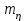 и дисперсию и дисперсию 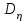 процесса процесса 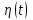 на выходе фильтра нижних частот, а далее вычислить плотность распределения вероятностей на выходе фильтра нижних частот, а далее вычислить плотность распределения вероятностей 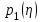 процесса процесса 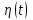 на выходе фильтра нижних частот для частного случая воздействия на коррелятор идентичных колебаний на выходе фильтра нижних частот для частного случая воздействия на коррелятор идентичных колебаний 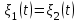 , т. е. при , т. е. при 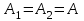 , , 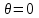 , , 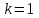 и и 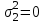 . .Решить эту задачу для случая отсутствия шума 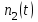 на втором входе коррелятора. на втором входе коррелятора.Решение Запишем сигнал на выходе умножителя: 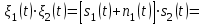 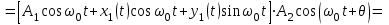 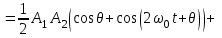 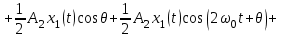 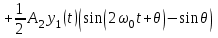 . (1) . (1)Здесь последнее слагаемое считалось следующим образом: 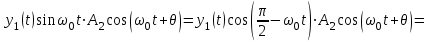 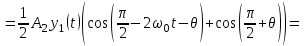 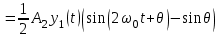 . .ФНЧ (полагаем, что это математический фильтр, т. е. идеальный), не пропустит на выход слагаемые, содержащие 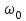 . .Тогда сигнал на выходе коррелятора имеет вид: 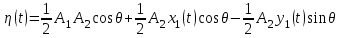 . (2) . (2)В выражении (2) нас интересует только первое слагаемое, поскольку остальные два в силу того, что гармонические колебания и квазигармонические флуктуации независимы, а значит мат. ожидание остальных слагаемых равно нулю. Запишем: 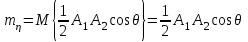 . .Найдем дисперсию 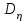 процесса процесса 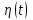 на выходе ФНЧ. Учитывая, что на выходе ФНЧ. Учитывая, что 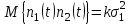 , запишем: , запишем: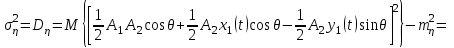 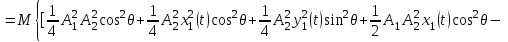 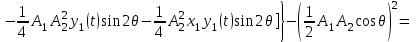 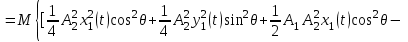 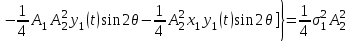 . .Плотность распределения вероятностей 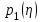 процесса процесса 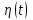 на выходе фильтра нижних частот для нормального закона и частного случая воздействия на коррелятор идентичных колебаний на выходе фильтра нижних частот для нормального закона и частного случая воздействия на коррелятор идентичных колебаний 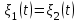 , т. е. при , т. е. при 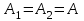 , , 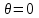 , , 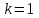 и и 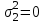 получим: получим: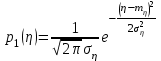 , (3) , (3)где 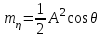 , , 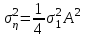 . . |
