РГЗ по МСиС. Задание 2 (2, С. 11) По выходным осциллограммам периодических сигналов, наблюдаемых на выходе исследуемого устройства, требуется выполнить следующие задания
 Скачать 88.25 Kb. Скачать 88.25 Kb.
|
|
Задание №2 ([2], С.11) По выходным осциллограммам периодических сигналов, наблюдаемых на выходе исследуемого устройства, требуется выполнить следующие задания: Построить в соответствии с исходными данными в линейном масштабе график исследуемого сигнала и произвести его аналитическое описание. Найти пиковое Um, среднее Uср, средневыпрямленное Uср.в и среднеквадратическое U значение напряжения наблюдаемого сигнала. Провести аналитическое описание переменной составляющей сигнала и построить ее график в том же масштабе, что и график исходного сигнала, и сравнить их. Найти пиковое  , среднее , среднее ,, средневыпрямленное ,, средневыпрямленное и среднеквадратическое и среднеквадратическое  значение напряжения переменной составляющей заданного выходного сигнала. значение напряжения переменной составляющей заданного выходного сигнала. Определить коэффициенты амплитуды Ka, формы Kф и усреднения Ky всего исследуемого сигнала и коэффициента амплитуды Ka, формы Kф и усреднения Ky его переменной составляющей. Найти показания вольтметров с различными типами преобразователей с закрытым (З) или открытым (О) входом в соответствии с заданием, если вольтметры проградуированы в среднеквадратических значениях для гармонического сигнала. Оценить пределы допускаемых абсолютной и относительной погрешностей показаний вольтметров, определенных в п.6 задания, если используемые измерительные приборы имеют класс точности  и конечное значение шкалы (предел измерения) Uк. и конечное значение шкалы (предел измерения) Uк.Оформить результаты измерений напряжений вольтметрами в соответствии с нормативными документами в двух вариантах: 1) с указанием границ абсолютной погрешности (расширенной неопределенности); 2) с указанием границ относительной погрешности, если измерения проведены в нормальных условиях. Исходные данные: (М =  ; N = ; N = ) )Таблица 1.1 – Исходные данные
Сигнал:  Решение: 1. Цель: построить в соответствии с исходными данными в линейном масштабе график исследуемого сигнала и произвести его аналитическое описание.  Рисунок 1.1. График исследуемого сигнала Сигнал, представленный на рисунке 1.1 можно описать следующим образом:  2. Цель: найти пиковое  , среднее , среднее 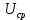 , средневыпрямленное , средневыпрямленное 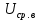 и среднеквадратическое и среднеквадратическое  значения напряжения наблюдаемого сигнала. значения напряжения наблюдаемого сигнала.Пиковое значение – наибольшее или наименьшее значение сигнала за время измерения: 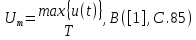 Где 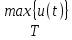 - операция нахождение максимального значения сигнала - операция нахождение максимального значения сигнала  на интервале измерения Т. на интервале измерения Т.Согласно варианту задания, за период Т=  мкс пиковое значение мкс пиковое значение  ; ; Среднее за время измерения T значение определяется выражением:     Рисунок 1.2. График модуля исследуемого сигнала за время измерения Средневыпрямленное за время измерения значение определяется выражением:    Среднеквадратическое за время измерения значение определяется выражением:    3. Цель: произвести аналитическое описание переменой составляющей сигнала и построить ее график в том же масштабе, что и график исходного сигнала, и сравнить их. Для того, чтобы вычислить переменную составляющую сигнала  нужно из сигнала вычесть среднее значение напряжения нужно из сигнала вычесть среднее значение напряжения 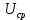 : :  Таким образом, получим аналитическое описание переменной составляющей выходного сигнала:  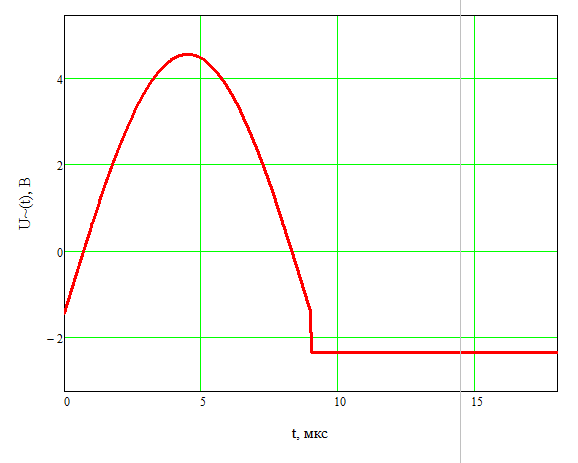 Рисунок 1.3. График переменной составляющей сигнала График переменной составляющей сигнала (Рисунок 1.3) смещается по оси напряжения вниз на размер среднего значения напряжения  . .4. Цель: найти пиковое  , среднее , среднее  , средневыпрямленное , средневыпрямленное  и среднеквадратическое и среднеквадратическое  значения напряжения переменной составляющей заданного выходного сигнала. значения напряжения переменной составляющей заданного выходного сигнала.Пиковое значение напряжения переменной составляющей заданного выходного сигнала: 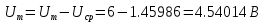 Среднее значение напряжения переменной составляющей заданного выходного сигнала  за время T определяется выражением: за время T определяется выражением:    Рисунок 1.4. График модуля переменной составляющей исследуемого сигнала за время измерения Средневыпрямленное значение напряжения переменной составляющей заданного выходного сигнала  за время измерения определяется выражением: за время измерения определяется выражением:   Среднеквадратическое значение напряжения переменной составляющей заданного выходного сигнала  за время измерения значения определяется выражением: за время измерения значения определяется выражением: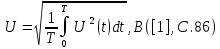  5. Цель: определить коэффициенты амплитуды 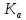 , формы , формы  и усреднения и усреднения 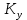 всего исследуемого сигнала и коэффициенты амплитуды всего исследуемого сигнала и коэффициенты амплитуды  , формы , формы  и усреднения и усреднения  его переменной составляющей. его переменной составляющей.Коэффициент амплитуды исследуемого сигнала определяется выражением:  Где  – пиковое значение ; – пиковое значение ;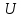 – среднеквадратическое значение. – среднеквадратическое значение. Коэффициент формы исследуемого сигнала определяется выражением:  Где 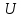 – среднеквадратическое значение ; – среднеквадратическое значение ; 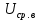 – средневыпрямленное значение. – средневыпрямленное значение.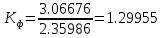 Коэффициент усреднения исследуемого сигнала определяется выражением: 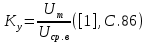 Где  – пиковое значение ; – пиковое значение ; 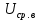 – средневыпрямленное значение. – средневыпрямленное значение.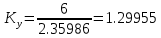 Для этих коэффициентов справедливо неравенство:   Коэффициент амплитуды переменной составляющей исследуемого сигнала определяется выражением:  Где  – пиковое значение переменной составляющей сигнала; – пиковое значение переменной составляющей сигнала; – среднеквадратическое значение переменной составляющей сигнала. – среднеквадратическое значение переменной составляющей сигнала.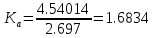 Коэффициент формы переменной составляющей исследуемого сигнала определяется выражением: 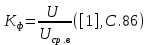 Где  – среднеквадратическое значение переменной составляющей сигнала ; – среднеквадратическое значение переменной составляющей сигнала ;  – средневыпрямленное значение переменной составляющей сигнала. – средневыпрямленное значение переменной составляющей сигнала. Коэффициент усреднения переменной составляющей исследуемого сигнала определяется выражением:  Где  – пиковое значение переменной составляющей сигнала; – пиковое значение переменной составляющей сигнала;  – средневыпрямленное значение переменной составляющей сигнала. – средневыпрямленное значение переменной составляющей сигнала. Для этих коэффициентов справедливо неравенство:   6. Цель: найти показания вольтметров с различными типами преобразователей с закрытым или открытым входом в соответствии с заданием, если вольтметры проградуированы в среднеквадратических значениях для гармонического сигнала. Показания пикового вольтметра с закрытым входом При закрытом входе вольтметр измеряет только переменную составляющую сигнала.  Где 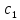 – градуировочный коэффициент для данного вольтметра – градуировочный коэффициент для данного вольтметра  , тогда: , тогда: Показания вольтметра с преобразователем среднеквадратического значения с открытым входом Показания вольтметра определяются формулой:  Где  – градуировочный коэффициент для данного вольтметра – градуировочный коэффициент для данного вольтметра  ([2], С.33), тогда: ([2], С.33), тогда: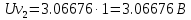 Показания вольтметра с преобразователем средневыпрямленных значений с открытым входом  Где  – градуировочный коэффициент для данного вольтметра – градуировочный коэффициент для данного вольтметра , тогда: , тогда: Показания вольтметра с преобразователем среднеквадратического значения с закрытым входом Показания вольтметра определяются формулой:  Где  – градуировочный коэффициент для данного вольтметра – градуировочный коэффициент для данного вольтметра тогда: тогда: 7. Цель: оценить пределы допускаемых абсолютной и относительной погрешностей (расширенных неопределенностей) показаний вольтметров, определенных в пункте 6 задания, если используемые измерительные приборы имеют класс точности  и конечное значение шкалы (предел измерения) и конечное значение шкалы (предел измерения)  , указанные в исходных данных. , указанные в исходных данных.Исходные данные:  , ,  % %Предел допускаемой абсолютной погрешности показаний вольтметров: 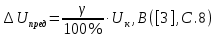  Предел допускаемой относительной погрешности показания вольтметра Uv1:   Погрешность округления составляет:  Погрешность округления не превышает 5%. Предел допускаемой относительной погрешности показания вольтметра Uv2:  Погрешность округления составляет:  Погрешность округления не превышает 5%. Предел допускаемой относительной погрешности показания вольтметра Uv3:  Погрешность округления составляет:  Погрешность округления не превышает 5%. Предел допускаемой относительной погрешности показания вольтметра Uv4:  Погрешность округления составляет:  Погрешность округления не превышает 5%. 8. Цель: оформить результаты измерений напряжения вольтметрами в соответствии с нормативными документами в двух вариантах: 1) с указанием границ абсолютной погрешности (расширенной неопределенности); 2) с указанием границ относительной погрешности, если измерения проведены в нормальных условиях.  ; ; ; ; P=0,997; условия измерения нормальные;  ; ; ; ; P=0,997; условия измерения нормальные;  ; ; ; ; P=0,997; условия измерения нормальные;  ; ; ; ; P=0,997; условия измерения нормальные; Список использованной литературы. Метрология, стандартизация и измерения в технике связи. Под редакцией Б.Г. Хромого, М., Радио и Связь, 1986г. Методические указания по выполнению индивидуального задания по курсам: метрология, стандартизация и сертификация; метрология и электрорадио измерения в телекоммуникационных системах; метрология и радиоизмерения; метрология, стандартизация и технические измерения. И.Н. Запасный, В.И. Сметанин, Новосибирск, 2012г Оценка инструментальных погрешностей при экспериментальных исследованиях. Методическое пособие под редакцией Н.И. Горлова, И.Н. Запасного, В.И. Сметанина, Новосибирск, 2015г. | ||||||||||||||||||||||||

 , мкс
, мкс