задание 2. Задание 2 Организация и методология сложных систем. Моделирование работы систем массового обслуживания Цель работы
 Скачать 123.33 Kb. Скачать 123.33 Kb.
|
|
Задание 2 «Организация и методология сложных систем. Моделирование работы систем массового обслуживания» Цель работы: Изучить методику моделирования систем массового обслуживания, оценить основные характеристики эффективности функционирования СМО. Задание: Изучить теоретический материал, приведенный в лекции. Кратко дать понятия «входной поток», «механизм обслуживания», «очередь заявок», «каналы». Оценить основные характеристики эффективности функционирования СМО, решив предложенные задания по варианту. Лабораторную работу оформить в виде отчета 14pt, 1.5 интервал, выравнивание по ширине. В отчете указать название, цели и задачи лабораторной работы, ход работы, полученные выводы. Ход выполнения работы: Обслуживаемый объект в теории систем массового обслуживания называется требованием или заявкой. В общем случае под требованием (заявкой) обычно понимают запрос на удовлетворение некоторой потребности. Роль требований или заявок выполняют клиенты, посетители, покупатели, документы, товары, суда и т.д. Средства, обслуживающие требования (заявки), называются обслуживающими устройствами или каналами обслуживания. Роль каналов обслуживания играют кассиры, специалисты, каналы телефонной связи, товароведы, компьютеры, мастера-ремонтники, погрузочно-разгрузочные точки на базах и складах и т.д. Требования (заявки) поступают в систему массового обслуживания (СМО) обычно не регулярно, а случайно, образуя так называемый случайный поток требований (заявок). Обслуживание заявок, вообще говоря, также продолжается какое-то случайное время. Случайный характер потока заявок и времени обслуживания приводит к тому, что СМО оказывается загруженной неравномерно: в какие-то периоды времени скапливается очень большое количество заявок (либо они становятся в очередь, либо покидают СМО необслуженными), в другие же периоды СМО работает с недогрузом или простаивает. Предметом теории массового обслуживания является установление зависимостей между характером потока заявок, числом каналов обслуживания, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Основной задачей теории массового обслуживания является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Задачи теории массового обслуживания носят оптимизационный характер и в конечном итоге включают экономический аспект по определению такого варианта системы, при котором будет обеспечен минимум суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на обслуживание и от простоев каналов обслуживания. В качестве показателей эффективности работы СМО используются: - абсолютная пропускная способность системы (А), т.е. среднее число заявок, обслуживаемых в единицу времени; -относительная пропускная способность (Q), т.е. средняя доля поступивших заявок, обслуживаемых системой; -вероятность отказа (Рот), т.е. вероятность того, что заявка покинет СМО не обслуженной; - среднее число занятых каналов (£); - среднее число заявок в СМО ( L c.); - среднее время пребывания заявки в системе (Тс); - среднее число заявок в очереди (4 ) - длина очереди; - среднее число заявок в системе (Lсист); - среднее время пребывания заявки в очереди ( Т0 ); - среднее время пребывания заявки в системе (Tсист) - степень загрузки канала ( Рзан ), т.е. вероятность того, что канал занят; - среднее число заявок, обслуживаемых в единицу времени; - среднее время ожидания обслуживания; - вероятность того, что число заявок в очереди превысит определенное значение и т.п. Моделирование и анализ одноканальной СМО Рассмотрим одноканальную СМО с отказами и показатели ее эффективности (основные характеристики ее работы, операционные характеристики). Имеется один канал, на который поступает поток заявок с интенсивностью λ. Поток обслуживании имеет интенсивность р. Предполагается, что все потоки событий, переводящие СМО из состояния в состояние, будут простейшими. Найти предельные вероятности состояний системы и показатели ее эффективности. В качестве показателей эффективности одноканальной СМО с отказами будем рассматривать: А - абсолютную пропускную способность СМО; Q - относительную пропускную способность; Ротк - вероятность отказа. Размеченный граф состояний представлен на рисунке 1. 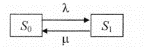 Рисунок 1. Одноканальная СМО с отказами S0- канал обслуживания свободен; S1 - канал обслуживания занят: λ - интенсивность потока заявок; µ - интенсивность потока обслуживания. В предельном стационарном режиме система алгебраических уравнений имеет вид: 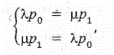 т.е. система вырождается в одно уравнение. Учитывая, что ро+p1 = 1, найдем предельные вероятности состояний: 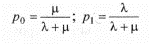 которые выражают среднее относительное время пребывания системы в состоянии S0, когда канал свободен, и S1, когда канал занят, т.е. определяют соответственно относительную пропускную способность Q системы и вероятность отказа: 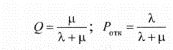 Абсолютная пропускная способность равна: A=λQ Пример. В парикмахерской работает один мастер. Время обслуживания распределено по показательному закону со средним 10 мин. Клиент, пришедший в парикмахерскую, когда мастер занят, не ожидает обслуживания, а покидает парикмахерскую. Поток клиентов - простейший с интенсивностью 8 клиентов/ч. Найти показатели эффективности работы данной парикмахерской. Решение. Имеем λ=8 (клиентов/ч.), среднее время обслуживания to6- 12(мин) = 0,2(ч.). Следовательно, интенсивность потока обслуживании µ= 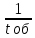 = 5(1/ч). По рассмотренным выше формулам получаем, относительная пропускная способность Q=0,38, то есть в среднем 38% поступающих клиентов будут обслужены. Соответственно вероятность отказа в обслуживании составит РОТК=0,62 (т.е. 0.62 %). Абсолютная пропускная способность СМО = 5(1/ч). По рассмотренным выше формулам получаем, относительная пропускная способность Q=0,38, то есть в среднем 38% поступающих клиентов будут обслужены. Соответственно вероятность отказа в обслуживании составит РОТК=0,62 (т.е. 0.62 %). Абсолютная пропускная способность СМО А=8* 0,38=3,04, то есть в среднем в час будут обслужены 3 клиента. Аналогично решить задачи для своего варианта. 1. Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин с одним каналом (одной группой проведения осмотра). На осмотр и выявление дефектов каждой машины затрачивается в среднем t часа. На осмотр поступает в среднем m машин в сутки. Потоки заявок и обслуживании - простейшие. Если машина, прибывшая в пункт осмотра, не застает ни одного канала свободным, она покидает пункт осмотра необслуженной. Определить предельные вероятности состояний и характеристики обслуживания профилактического пункта осмотра и сделайте вывод об эффективности его работы. Варианты распределяются в зависимости от номера студента в списке группы следующим образом:
2. Одноканальная СМО с отказами представляет собой одну телефонную линию, на вход которой поступает простейший поток вызовов с интенсивностью t вызовов/мин. Средняя продолжительность разговора m мин.; время разговора имеет показательное распределение. Найти предельные вероятности состояний и характеристики обслуживания СМО. Сравнить пропускную способность СМО с номинальной, которая была бы, если разговор в точности 3 мин., а заявки шли одна за другой регулярно, без перерывов.
2. Моделирование и анализ замкнутых СМО Замкнутая система массового обслуживания -это система массового обслуживания, в которой есть фиксированное число источников заявок. Поток заявок каждого источника имеет одинаковую интенсивность. Первоначальный поток заявок имеет интенсивность большую в «число источников» - раз, чем поток заявок от одного источника. Иными словами, если работа источника заявок не зависит от состояния СМО, то такие СМО называются открытыми (разомкнутыми), т.е. это такие СМО, в которых заявки поступают извне. Если источник меняет свою работу в зависимости от состояния, СМО называется замкнутой (есть обратная связь). Рассмотрим следующий пример. Бригада из m работников обслуживает n единиц оборудования (m t̅об = 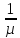 , где , гдеµ - интенсивность потока обслуживаний. Тогда граф состояний для замкнутой СМО выглядит следующим образом: 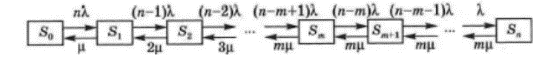 Пусть λ - интенсивность потока неисправностей одной единицы оборудования. Перечислим состояния: So-все оборудование исправно, работники свободны; S1-одна единица оборудования неисправна, один работник его ремонтирует; ... Sm-m единиц оборудования неисправны, m работников их ремонтируют; ... Sn – n единиц оборудования неисправны, m единиц оборудования ремонтируются, а (n-m) ожидают ремонта. Тогда предельные вероятности состояний: 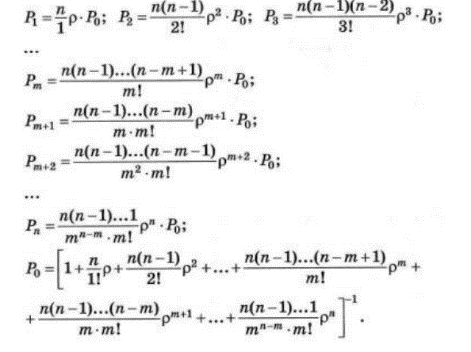 Где: Таблица 1
Работу замкнутой СМО выполнить по варианту. В состав оборудования вычислительного центра входит n независимо круглосуточно работающих ЭВМ. Обслуживание ЭВМ производится группой из m специалистов. С учетом 8 часового рабочего дня при трехсменной работе приходится планировать всего 3m человек. Каждая ЭВМ может выйти из строя λ раз в месяц. Вышедшая из строя ЭВМ останавливается и , если в этот момент все специалисты заняты, становится в очередь на обслуживание и ждет пока любой из специалистов освободится. Среднее время ремонта tр известно. Убытки, связанные с одним часом простоя составляют N рублей. Месячная зарплата одного специалиста M рублей. Принять, что в месяце 30 рабочих дней. Определить, какое требуется количество специалистов в штате вычислительного центра, чтобы минимизировать месячные затраты S на обслуживание с учетом потерь от простоя ЭВМ. Объяснить, что для этого необходимо найти m, при которой обеспечивается S = (ср. число неисправных ЭВМ) ∙ N∙(24час)∙(30дней) + 3m ⋅ M −>min 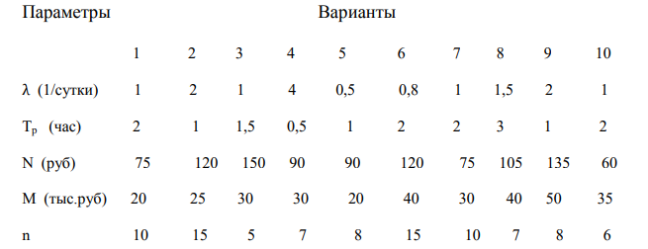 Варианты распределяются в зависимости от номера студента в списке группы следующим образом:
Рассчитать по своему варианту характеристики работы СМО по таблице 1. Контрольные вопросы: Приведите примеры одноканальных и многоканальных СМО. Какие показатели эффективности можно рассчитать для одноканальных СМО с неограниченной очередью? Какие показатели эффективности можно рассчитать для замкнутых СМО? |

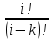 pk.p0;k=1,…i
pk.p0;k=1,…i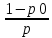 =
=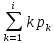
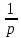
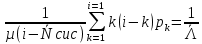 N̅сис
N̅сис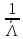 N̅сис
N̅сис