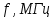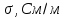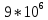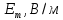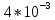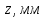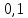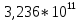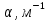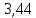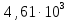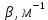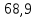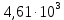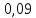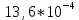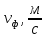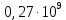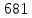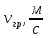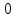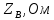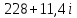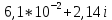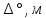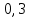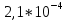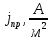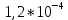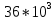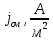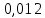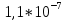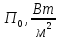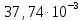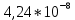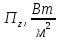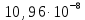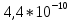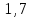Задание 2
 Скачать 39.77 Kb. Скачать 39.77 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ Федеральное государственное бюджетное учреждение высшего образования «Омский государственный технический университет» Радиотехнический факультет Кафедра «Средства связи и информационная безопасность» «Задание №2» Выполнили студенты 3-го курса, группы БИТ-191 Булычев А.Е. Вульферт Н.И. ________________________ (подпись) Принял Доцент Михеев В.В. ________________________ (подпись) Омск, 2021 Задание №2 Вариант 23 Плоская гармоническая ЭМВ с частотой 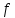 , распространяется вдоль оси , распространяется вдоль оси 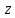 в проводящей среде с параметрами в проводящей среде с параметрами 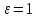 , , 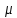 , , 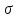 . Амплитуда вектора . Амплитуда вектора 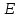 в начале координат равна в начале координат равна 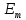 . .Найти 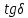 , коэффициент затухания и фазы, , коэффициент затухания и фазы, 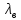 , , 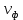 , , 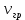 , волновое сопротивление среды, глубину проникновения ЭМВ в вещество. Определить амплитуду плотности тока проводимости и смещения, а также плотность потока мощности волны в начале координат и на расстоянии , волновое сопротивление среды, глубину проникновения ЭМВ в вещество. Определить амплитуду плотности тока проводимости и смещения, а также плотность потока мощности волны в начале координат и на расстоянии 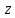 от начала координат. Рассчитать на каком расстоянии от начала координат амплитуда поля уменьшается в от начала координат. Рассчитать на каком расстоянии от начала координат амплитуда поля уменьшается в 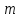 раз. раз.Сравнить полученные результаты с заданием 1, сделать выводы.
Тангенс угла диэлектрических потерь 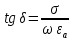 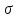 – удельная проводимость – удельная проводимость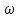 – циклическая частота – циклическая частота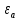 – абсолютная диэлектрическая проницаемость – абсолютная диэлектрическая проницаемостьНайдем циклическую частоту: 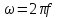 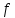 – частота – частота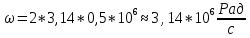 Найдем тангенс угла диэлектрических потерь: 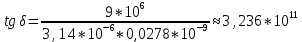 Так как 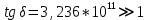 , то средой ЭМП является проводник. , то средой ЭМП является проводник.Коэффициент затухания 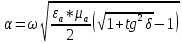 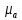 – абсолютная магнитная проницаемость – абсолютная магнитная проницаемостьТак как средой ЭМП является проводник, то в формуле коэффициента затухания можно пренебречь «1»: 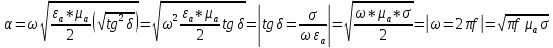 Найдем коэффициент затухания: 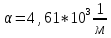 Коэффициент фазы 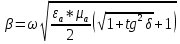 Так как средой ЭМП является проводник, то в формуле коэффициента фазы можно пренебречь «1», получим, что: 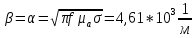 Длина волны 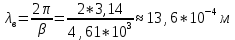 Фазовая скорость 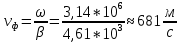 Групповая скорость При прохождении в проводнике расстояния, равного 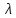 , ЭМВ испытывает очень большое затухание , ЭМВ испытывает очень большое затухание 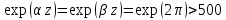 . Поэтому можно говорить о том, что пространственная периодичность поля плоской ЭМВ в проводнике отсутствует, и можно считать, что . Поэтому можно говорить о том, что пространственная периодичность поля плоской ЭМВ в проводнике отсутствует, и можно считать, что 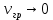 . .Волновое сопротивление среды Волновое сопротивление проводника имеет примерно одинаковые по модулю активную и реактивную части, поскольку при 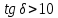 для проводников для проводников 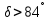 . Комплексное волновое сопротивление проводника имеет активно-индуктивный характер, поскольку . Комплексное волновое сопротивление проводника имеет активно-индуктивный характер, поскольку 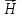 отстает по фазе от отстает по фазе от 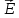 на на 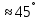 : :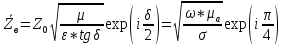 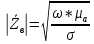 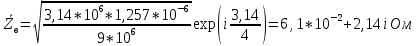 Глубина проникновения ЭМП в вещество 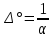 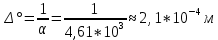 Амплитуда плотности тока проводимости 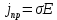 Так как амплитуда вектора 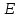 в начале координат равна в начале координат равна 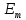 , то , то 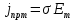 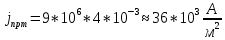 Амплитуда плотности тока смещения 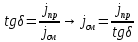 Так как амплитуда вектора 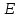 в начале координат равна в начале координат равна 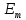 , то , то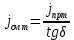 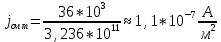 Плотность потока мощности волны в начале координат Плотность потока мощности 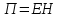 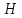 – напряжённость магнитного поля – напряжённость магнитного поляТак как амплитуда вектора 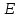 в начале координат равна в начале координат равна 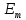 , то плотность потока мощности волны в начале координат имеет вид: , то плотность потока мощности волны в начале координат имеет вид: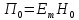 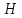 – напряжённость магнитного поля в начале координат – напряжённость магнитного поля в начале координатНайдем напряжённость магнитного поля в начале координат: 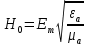 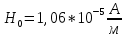 Найдем плотность потока мощности волны в начале координат: 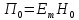 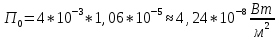 Плотность потока мощности волны на расстоянии 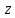 от начала координат от начала координат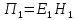 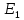 – напряженность электрического поля на расстоянии – напряженность электрического поля на расстоянии 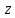 от начала координат от начала координат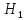 – напряжённость магнитного поля на расстоянии – напряжённость магнитного поля на расстоянии 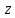 от начала координат от начала координатОслабление 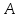 показывает затухание ЭМВ при распространении ее вдоль оси показывает затухание ЭМВ при распространении ее вдоль оси 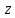 : :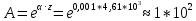 Также 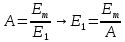 Найдем напряженность электрического поля на расстоянии 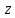 от начала координат: от начала координат: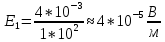 Найдем напряжённость магнитного поля на расстоянии 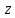 от начала координат: от начала координат: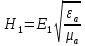 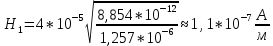 Найдем плотность потока мощности волны на расстоянии 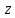 от начала координат от начала координат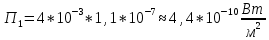 Расстояние от начала координат, на котором амплитуда поля уменьшается в 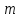 раз. раз.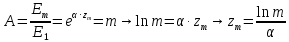 Найдем расстояние от начала координат, на котором амплитуда поля уменьшается в 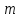 раз: раз: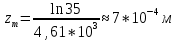
Вывод: в ходе выполнения лабораторной работы, мы нашли тангенс угла диэлектрических потерь ( 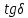 ), коэффициент затухания и фазы, длину волны, фазовую и групповую скорости, волновое сопротивление среды и глубину проникновения ЭМВ в вещество. Определили амплитуду плотности тока проводимости и смещения, а также плотность потока мощности волны в начале координат и на расстоянии ), коэффициент затухания и фазы, длину волны, фазовую и групповую скорости, волновое сопротивление среды и глубину проникновения ЭМВ в вещество. Определили амплитуду плотности тока проводимости и смещения, а также плотность потока мощности волны в начале координат и на расстоянии 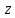 от начала координат. Рассчитали на каком расстоянии от начала координат амплитуда поля уменьшается в от начала координат. Рассчитали на каком расстоянии от начала координат амплитуда поля уменьшается в 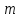 раз. раз. |