Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25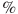 этих стекол, вторая — 75 этих стекол, вторая — 75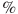 . Первая фабрика выпускает 4 . Первая фабрика выпускает 4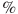 бракованных стекол, а вторая — 2 бракованных стекол, а вторая — 2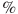 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
|
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70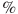 этих стекол, вторая — 30 этих стекол, вторая — 30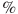 . Первая фабрика выпускает 1 . Первая фабрика выпускает 1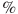 бракованных стекол, а вторая — 3 бракованных стекол, а вторая — 3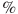 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
|
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30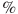 этих стекол, вторая — 70 этих стекол, вторая — 70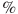 . Первая фабрика выпускает 4 . Первая фабрика выпускает 4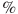 бракованных стекол, а вторая — 1 бракованных стекол, а вторая — 1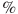 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
|
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70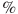 этих стекол, вторая — 30 этих стекол, вторая — 30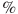 . Первая фабрика выпускает 5 . Первая фабрика выпускает 5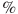 бракованных стекол, а вторая — 4 бракованных стекол, а вторая — 4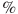 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
|
Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
|
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,25. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,1. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
|
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,35. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
|
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Внешние углы», равна 0,2. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,3. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
|
Задание (№ 320385)
|
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,1. Вероятность того, что это вопрос на тему «Тригонометрия», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
|
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
|
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
|
В аэропорте два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
|
В аэропорте два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,4. Вероятность того, что кофе закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
|
Задание (№ 320471)
|
|
|
|
Биатлонист 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.
|
Биатлонист 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последний промахнулся. Результат округлите до сотых.
|
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
|
Биатлонист 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.
|
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,12 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
|
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,02 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
|
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,1 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
|
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,07 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен
|
Задание (№ 320583)
|
|
|
|
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,21. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
|
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,07. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
|
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,19. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
|
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,22. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
|
Вероятность того, что новый сканер прослужит больше года, равна 0,9. Вероятность того, что он прослужит больше двух лет, равна 0,88. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
|
Вероятность того, что новый пылесос прослужит больше года, равна 0,92. Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
|
Вероятность того, что новый персональный компьютер прослужит больше года, равна 0,95. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
|
Задание(№ 320649)
|
|
|
|
Вероятность того, что новый сканер прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
|
Задание (№ 320741)
|
|
|
|
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 60% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 70% яиц высшей категории. Всего высшую категорию получает 65% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
|
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 90% яиц высшей категории. Всего высшую категорию получает 60% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
|
Задание (№ 320745)
|
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 55% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 35% яиц высшей категории. Всего высшую категорию получает 45% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
|
Задание (№ 320747)
|
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 50% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 70% яиц высшей категории. Всего высшую категорию получает 65% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
|
Задание (№ 320959)
|
|
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,3. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
|
Ковбой Джон попадает в муху на стене с вероятностью 0,7, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,1. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
|
Задание (№ 320963)
|
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,1. На столе лежит 10 револьверов, из них только 3 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
|
Ковбой Джон попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежит 10 револьверов, из них только 3 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
|
Задание (№ 321163)
|
|
|
|
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 8 очков в двух играх. Если команда выигрывает, она получает 5 очков, в случае ничьей — 3 очка, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.
|
Задание (№ 321165)
|
|
|
|
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 6 очков в двух играх. Если команда выигрывает, она получает 4 очка, в случае ничьей — 2 очка, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.
|
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 6 очков в двух играх. Если команда выигрывает, она получает 5 очков, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
|
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 9 очков в двух играх. Если команда выигрывает, она получает 5 очков, в случае ничьей — 4 очка, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
|
При изготовлении подшипников диаметром 61 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,972. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 60,99 мм, или больше, чем 61,01 мм.
|
При изготовлении подшипников диаметром 65 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,981. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 64,99 мм, или больше, чем 65,01 мм.
|
При изготовлении подшипников диаметром 60 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,972. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 59,99 мм, или больше, чем 60,01 мм.
|
При изготовлении подшипников диаметром 72 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,971. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 71,99 мм, или больше, чем 72,01 мм.
|
Задание (№ 321791)
|
|
|
|
Вероятность того, что на тесте по истории учащийся Т. верно решит больше 8 задач, равна 0,76. Вероятность того, что Т. верно решит больше 7 задач, равна 0,88. Найдите вероятность того, что Т. верно решит ровно 8 задач.
|
Задание (№ 321793)
|
Вероятность того, что на тесте по математике учащийся У. верно решит больше 12 задач, равна 0,78. Вероятность того, что У. верно решит больше 11 задач, равна 0,88. Найдите вероятность того, что У. верно решит ровно 12 задач.
|
Задание (№ 321795)
|
|
Вероятность того, что на тесте по истории учащийся Т. верно решит больше 9 задач, равна 0,68. Вероятность того, что Т. верно решит больше 8 задач, равна 0,78. Найдите вероятность того, что Т. верно решит ровно 9 задач.
|
Задание (№ 321797)
|
Вероятность того, что на тесте по истории учащийся Т. верно решит больше 8 задач, равна 0,58. Вероятность того, что Т. верно решит больше 7 задач, равна 0,64. Найдите вероятность того, что Т. верно решит ровно 8 задач.
|
Задание (№ 321895)
|
Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 68 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Менеджмент», нужно набрать не менее 68 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент Р. получит не менее 68 баллов по математике, равна 0,7, по русскому языку — 0,7, по иностранному языку — 0,8 и по обществознанию — 0,5.
Найдите вероятность того, что Р. сможет поступить на одну из двух упомянутых специальностей.
|
Задание (№ 321897)
|
|
Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 64 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Социология», нужно набрать не менее 64 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент Б. получит не менее 64 баллов по математике, равна 0,5, по русскому языку — 0,9, по иностранному языку — 0,8 и по обществознанию — 0,9.
Найдите вероятность того, что Б. сможет поступить на одну из двух упомянутых специальностей.
|
Задание (№ 321899)
|
Чтобы поступить в институт на специальность «Международные отношения», абитуриент должен набрать на ЕГЭ не менее 67 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Менеджмент», нужно набрать не менее 67 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент Т. получит не менее 67 баллов по математике, равна 0,6, по русскому языку — 0,5, по иностранному языку — 0,8 и по обществознанию — 0,9.
Найдите вероятность того, что Т. сможет поступить на одну из двух упомянутых специальностей.
|
Задание (№ 321901)
|
Чтобы поступить в институт на специальность «Международные отношения», абитуриент должен набрать на ЕГЭ не менее 79 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 79 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент И. получит не менее 79 баллов по математике, равна 0,8, по русскому языку — 0,7, по иностранному языку — 0,9 и по обществознанию — 0,5.
Найдите вероятность того, что И. сможет поступить на одну из двух упомянутых специальностей.
|
По отзывам покупателей Василий Васильевич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,93. Вероятность того, что этот товар доставят из магазина Б, равна 0,94. Василий Васильевич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
|
По отзывам покупателей Пётр Петрович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,87. Вероятность того, что этот товар доставят из магазина Б, равна 0,92. Пётр Петрович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
|
По отзывам покупателей Василий Васильевич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,88. Василий Васильевич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
|
Задание (№ 322005)
|
По отзывам покупателей Василий Васильевич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,83. Василий Васильевич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
|
Задание (№ 322101)
|
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,81. Вероятность того, что окажется меньше 12 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 12 до 19.
| |
 Скачать 52.01 Kb.
Скачать 52.01 Kb.