Задание. Задание 4
 Скачать 94.05 Kb. Скачать 94.05 Kb.
|
Задание №4Численное дифференцирование. Интерполяционные многочлены Ньютона, Лагранжа, формулы Стирлинга. Для функции 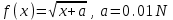 , где N=6, составить таблицу значений функции для аргументов , где N=6, составить таблицу значений функции для аргументов 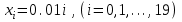 По значениям функции в этой таблице найти значения первой и второй производных указанной функции в точках 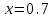 и и 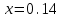 с точностью с точностью 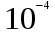 , ,используя: а) интерполяционный многочлен Лагранжа; б) интерполяционный многочлен Ньютона; в) формулу Стирлинга. Решение: Численное дифференцирование. При решении практических задач необходимо найти производные указанных порядков от функции 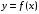 , которая задана таблицей значений , которая задана таблицей значений 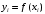 . Приблизим функцию . Приблизим функцию 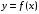 интерполяционным многочленом интерполяционным многочленом 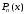 . Тогда производная от этого многочлена . Тогда производная от этого многочлена 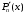 применяется для приближенного представления искомой производной применяется для приближенного представления искомой производной 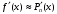 . .Составим таблицу значений функции в указанных узловых точках (таблица 1):
Продолжение таблицы 1
Интерполяционные многочлены Лагранжа. Дифференцирование интерполяционных многочленов Лагранжа приводит к формулам: 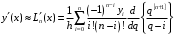 (1) (1)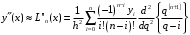 , (2) , (2)где 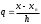 ; ; 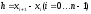 . .По формулам (1) и (2) найдем значения производных функции 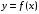 в точках в точках 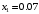 и и 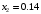 . .Таблица 2 – Значения производных по формуле Лагранжа в точке 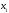
Продолжение таблицы 2
Таблица 3 – Значения производных по формуле Лагранжа в точке 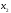
Интерполяционные многочлены Ньютона. Дифференцирование интерполяционных многочленов Ньютона приводит к формулам: 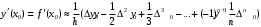 (3) (3)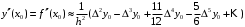 (4) (4)По формулам (3) и (4) найдем значения производных функции 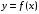 в точках в точках 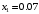 и и 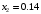 . .Таблица 4 – Значения производных по формуле Ньютона в точке 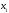
Таблица 5 – Значения производных по формуле Ньютона в точке 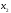
Формула Стирлинга. Дифференцирование интерполяционных многочленов Стирлинга приводит к формулам: 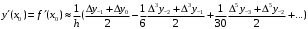 (5) (5)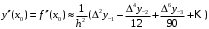 (6) (6)По формулам (5) и (6) найдем значения производных функции 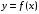 в точках в точках 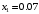 и и 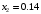 . .Таблица 6 – Значения производных по формуле Стирлинга в точке 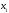
Таблица 7 – Значения производных по формуле Стирлинга в точке 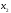
Вывод: В данной лабораторной работе мы нашли значения первой и второй производных с помощью интерполяционных многочленов Лагранжа, Ньютона и Стирлинга. Более точный результат даёт формула Стирлинга. |


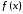
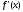
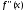
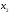 =0.14
=0.14