Задание 7 огэ математика. Задание 7 из ОГЭ по математике. Задание 7 из огэ по математике
 Скачать 143.13 Kb. Скачать 143.13 Kb.
|
|
Задание 7 из ОГЭ по математике 1. Если a > b и b > c, то a > c 2. Если a > b и c — любое число, то a + c > b + c Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство. 3. Если a > b и c — положительное число (с > 0), то ac > bc Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство. 4. Если a > b и c — отрицательное число (с ˂ 0), то ac ˂ bc Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный. 5. Если a ˂ b, и a и b — положительные числа, то 1/a > 1/b. Задание 7 «Числовые неравенства, координатная прямая» включает в себя следующие типы задач: 1.Неравенства Пример 1. 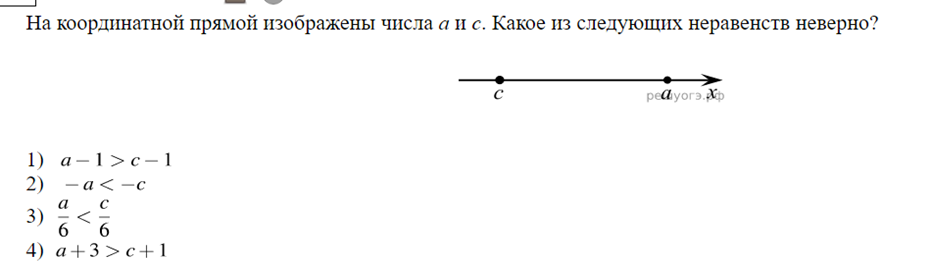 Решение: На координатной прямой мы видим, что a > c. Проверим каждое из приведённых неравенств. 1) Неравенство a – 1 > c – 1 равносильно неравенству a – 1 + 1 > c – 1 + 1 (по свойству 2 прибавим к обеим частям неравенства одно и то же число 1), . Получим a > c. Это верное равенство. 2) Неравенство – a ˂ – c, по свойству 4 умножим обе части неравенства на (– 1), при этом знак неравенства изменится. Получим a > c. Это верное равенство. 3) Неравенство a/6 ˂ c/6, по свойству 3 умножим обе части неравенства на 6, a/6 × 6 ˂ c/6 × 6. Сокращаем на 6, получаем неравенство a ˂ c, это неверно, противоречит условию, так как a > c. 4) a + 3 > c + 1. Прибавим к обеим частям неравенства (– 3). Получим a + 3 – 3> c + 1 – 3, a > c – 2, это верное неравенство, так как по условию a > c. Итак, неверным является вариант ответа под номером 3, его и пишем в ответ. Ответ: 3. 2.Сравнение чисел Пример 2. Решение: Прежде, чем сравнивать числа x и y, приведём их к одному виду. 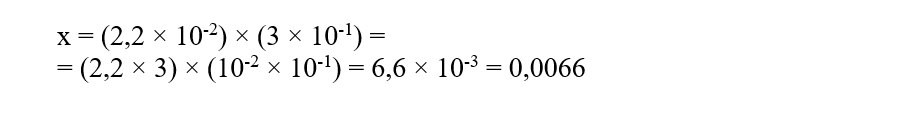 Итак, теперь сравним числа x = 0,0066 и y = 0,007. В нашем примере сравнение идёт по цифрам разряда тысячных. Получаем, что 0,0066 ˂ 0,007. Ответ: 0,0066. Пример 3. 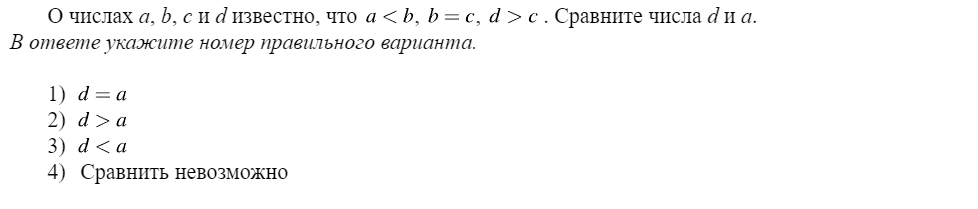 Решение: Расположим числа a, b, c и d в порядке возрастания, исходя из условий: а меньше b b равно c d больше c Таким образом, в порядке возрастания числа будут расположены так: a, b (= c), d. А, значит, d — самое большее из чисел, и d > a Это вариант ответа 2). Ответ: 2. Пример 4.  Решение: На примере этого задания покажу способ, который я иногда предлагаю тем ребятам, которым сложно анализировать. Я предлагаю им, взять любые числа, удовлетворяющие условию задачи, и работать непосредственно с ними, проверяя варианты ответов. Итак, известно a ˂ b ˂ 0, оба числа меньше нуля, и причём a ˂ b. Например, возьмём a = – 4, b = –3. 1) a – 1 = – 4 –1 = –5 2) b – 1 = – 3 – 1 = – 4 3) a × b = (– 4) × ( –3) = 12 4) (– b) = (– (– 3)) = 3 Осталось только выбрать наименьшее число из получившихся ответов, это (–5), а значит правильный вариант — под номером 1. Ответ: 1. Такой способ можно применить и в примерах 1 и 3. 3.Числа на прямой Пример 5. 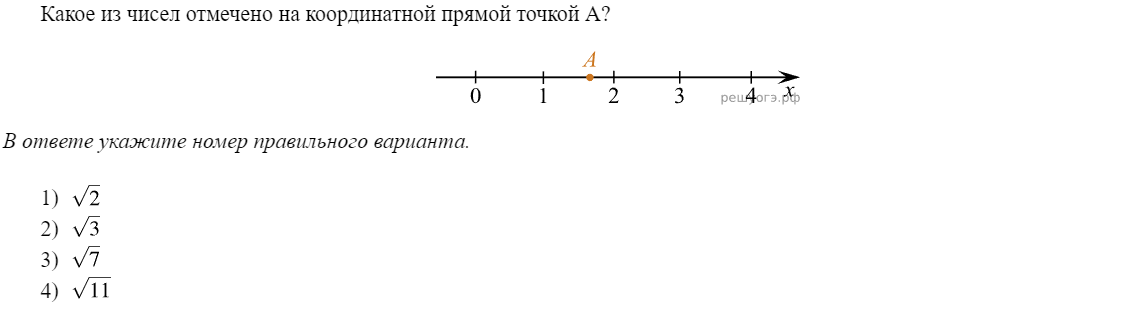 Решение: Точка А расположена между 1 и 2, но ближе к 2. Оценим приведённые варианты ответов:  Ответ: 2. 4.Выбор верного или неверного утверждения Пример 6  Решение: Как видно из координатной прямой x — число отрицательное, а у — положительное, значит, x ˂ y, при этом число x расположено ближе к началу координат, а значит, модуль числа x меньше модуля числа y. Таким образом, правильный вариант ответа под номером 1. Ответ: 1., |
