матан. Задание 8 Решить систему уравнений тремя способами. По формулам Крамера
 Скачать 239.69 Kb. Скачать 239.69 Kb.
|
ОглавлениеЗадание №28 8 Задание №8 Решить систему уравнений тремя способами. 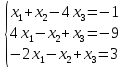 По формулам Крамера Запишем систему в матричной форме 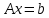 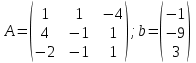 Вычислим  – определитель матрицы – определитель матрицы 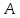 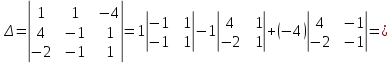 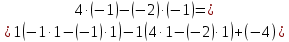 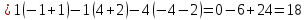 Заменим столбец 1 матрицы 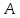 на вектор столбец на вектор столбец 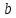 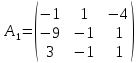 Вычислим 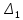 – определитель матрицы – определитель матрицы 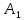 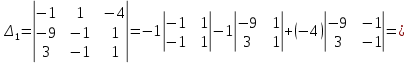 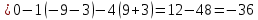 Заменим столбец 2 матрицы 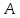 на вектор столбец на вектор столбец 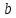 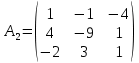 Вычислим 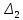 – определитель матрицы – определитель матрицы 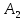 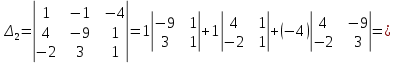 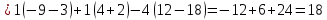 Заменим столбец 3 матрицы  на вектор столбец на вектор столбец  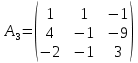 Вычислим  – определитель матрицы – определитель матрицы  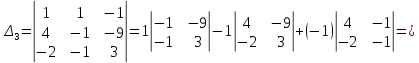 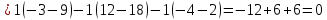 Т.к. главный определитель системы отличен от 0 вычислим  по формулам Крамера по формулам Крамера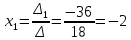 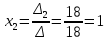 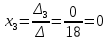 Метод Гаусса Для решения системы, построим расширенную матрицу 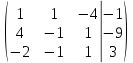 Исключим элементы 1-ого столбца матрицы ниже элемента 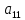 . Для этого сложим строки 2,3 со строкой 1, умноженной на -4 а затем на 2 соответственно: . Для этого сложим строки 2,3 со строкой 1, умноженной на -4 а затем на 2 соответственно: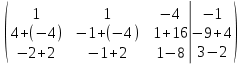 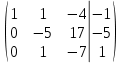 Исключим элементы 2-го столбца матрицы ниже элемента 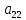 Для этого сложим строку 3 со строкой 2, умноженной на одну пятую Для этого сложим строку 3 со строкой 2, умноженной на одну пятую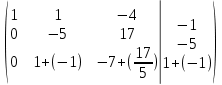 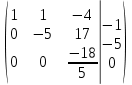 Из расширенной матрицы восстановим систему линейных уравнений 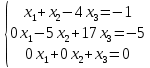 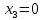 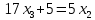 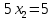 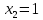 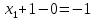 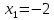 Матричный метод СЛАУ можно представить в виде 3 матриц 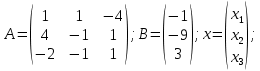 При этом 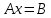 Умножим обе части уравнения на обратную матрицу 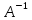 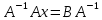 Так как 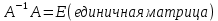 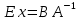 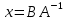 Условие существования обратной матрицы  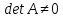 Соответственно вычислим детерминант матрицы (определитель) 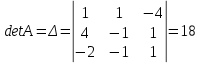 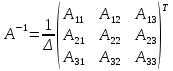 Для составления обратной матрицы вычислим алгебраические дополнения 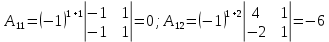  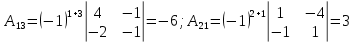 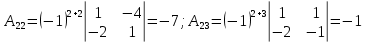 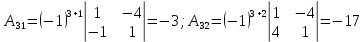 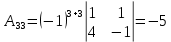 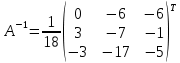 Транспонируем матрицу 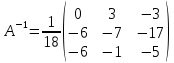 Проверим правильность вычислений 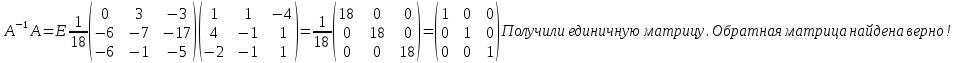 Воспользуемся ранее найденной формулой  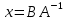 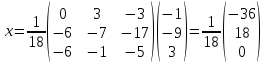 Ответ: 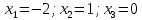 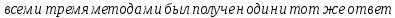 Задание №18 Даны векторы 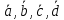 . Показать что векторы . Показать что векторы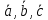 образуют базис и найти координаты вектора образуют базис и найти координаты вектора 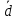 в этом базисе в этом базисе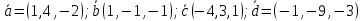 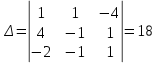 Определитель больше нуля, следовательно векторы вектора 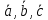 образуют базис образуют базис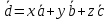 Для нахождения коэффициентов x,y,z составим СЛАУ 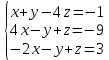 Решим по формулам Крамера (вычислено в задании №8) 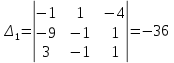 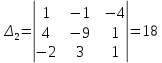 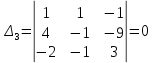 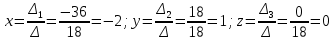 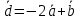 Задание №28Даны координаты вершины пирамиды 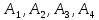 Найти: Найти:а) угол между рёбрами 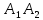 и и 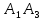 б) площадь грани 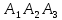 в) уравнение высоты, проходящей через 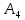 д) объём пирамиды  Даны координаты пирамиды Даны координаты пирамиды 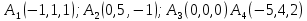 Найдем координаты векторов по формуле: 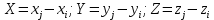 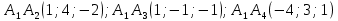 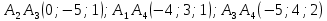 Рассчитаем модули векторов (длина ребер пирамиды) Длина вектора 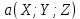 выражается через его координаты формулой выражается через его координаты формулой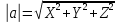 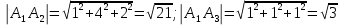 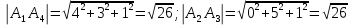 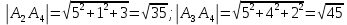 а) Вычислим угол между рёбрами 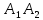 и и 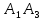 Угол между векторами 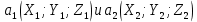 можно найти по формуле можно найти по формуле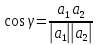 Где 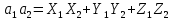 В нашем случае  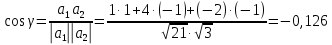 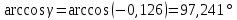 б) площадь грани Площадь грани можно найти по формуле 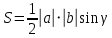 Где 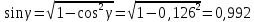 Площадь грани  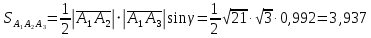 в) уравнение плоскости  Если точки 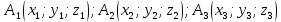 не лежат на одной прямой, то проходящая через них плоскость представляется уравнением не лежат на одной прямой, то проходящая через них плоскость представляется уравнением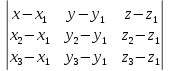 уравнение плоскости 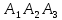 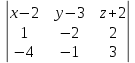 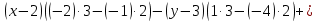 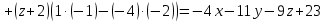 г) Уравнение высоты, проходящей через 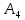 Прямая, проходящая через точку Прямая, проходящая через точку 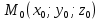 и перпендикулярную плоскости и перпендикулярную плоскости 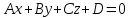 имеет направляющий вектор имеет направляющий вектор 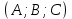 и, значит, представляется симметричными уравнениями: и, значит, представляется симметричными уравнениями:Т.к. Уравнение плоскости  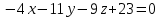 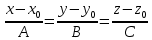 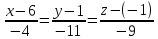 д) Объем пирамиды 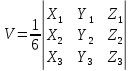 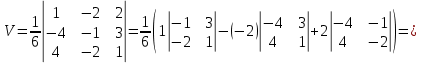 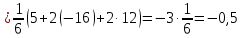 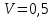 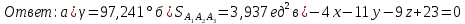 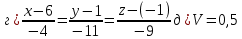 Задание №58 найти точку разрыва заданной функции. Сделать чертёж 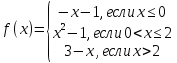 Исследуем точку стыка промежутков 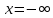 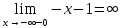 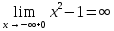 В этой точке функция терпит разрыв. Предел равен 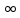 , поэтому это точка разрыва II-го рода. , поэтому это точка разрыва II-го рода. Исследуем поведение функции на отрезке 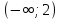 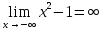 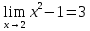 Пределы существуют, на указанном промежутке функция непрерывна. Исследуем точку стыка промежутков 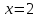 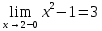 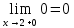 В этой точке пределы существуют, но они разные, поэтому это точка разрыва I-го рода. Исследуем поведение функции на отрезке 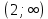 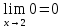 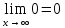 Пределы существуют, на указанном промежутке функция непрерывна. Ответ: Точка 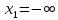 является точкой разрыва II-го рода. является точкой разрыва II-го рода. Точка 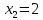 является точкой разрыва I-го рода. является точкой разрыва I-го рода. 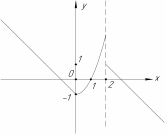 Задание №68 найти производные заданных функций 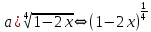 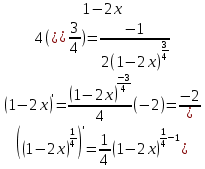 б) 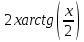 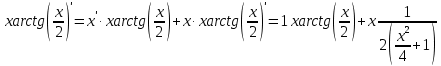 где 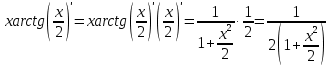 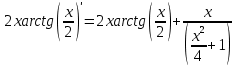 в) 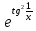 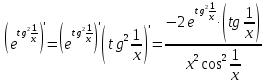 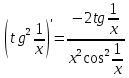 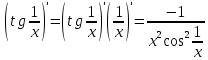 г) 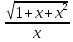 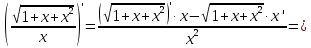 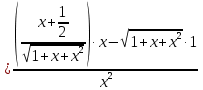 Здесь 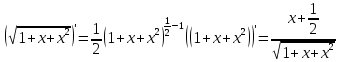 д) 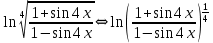 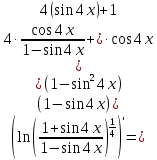 Поскольку 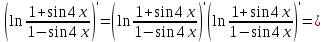 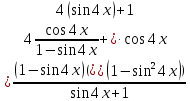 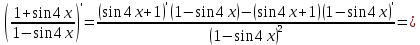 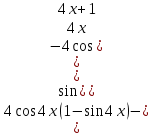 Задание №78. Вычислить производную степенно-показательной функции из пункта а), рассматривая эту функцию как суперпозицию функции двух переменных 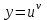 и функций одной переменной и функций одной переменной 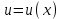 и и 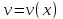 . Вычислить производную функции . Вычислить производную функции 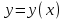 , неявно заданной уравнением , неявно заданной уравнением 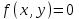 в пункте б), используя формулу в пункте б), используя формулу 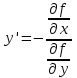 . . а) 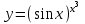 ; б) ; б) 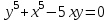 . .Решение. а) 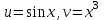 ; ; 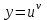 . .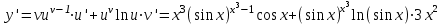 . .б) 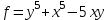 . . 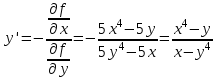 . .Задание №98. Найти наибольшее и наименьшее значения функции на данном отрезке. 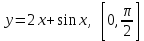 . .Решение. Точки, в которых функция принимает наибольшее и наименьшее значения, ищем сначала, приравнивая производную функции к нулю: 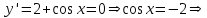 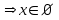 . Найдем значение функции на концах отрезка: . Найдем значение функции на концах отрезка: 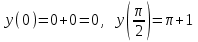 . Значит, . Значит, 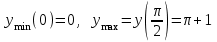 . .Задание №138. Исследовать функцию 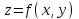 на экстремум и вычислить производную этой функции в точке М по направлению вектора на экстремум и вычислить производную этой функции в точке М по направлению вектора 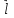 . .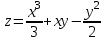 ; М(0,2); ; М(0,2); 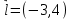 . .Решение. Найдем стационарные точки из системы: 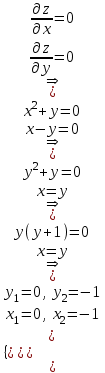 . .(-1,-1) и (0,0) – стационарные точки. 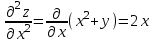 , , 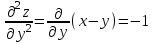 , , 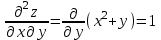 . .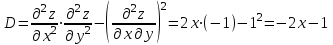 . .Для точки (-1,-1): 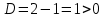 , , 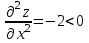 . .Для точки (0,0): 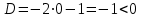 . .(-1,-1) – точка максимума. 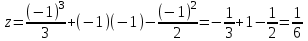 . .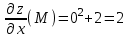 , , 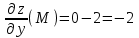 . .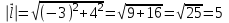 ; ; 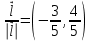 . . 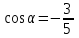 ; ; 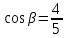 . .Производная в точке М в направлении вектора 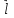 равна: равна: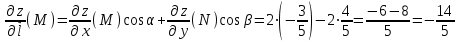 . .Задание №148 Вычислить интегралы 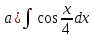 б) б) 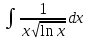 ; в) ; в) 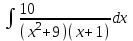 ; г) ; г) 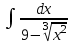 ; д) ; д) 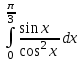 ; e) ; e) 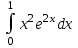 . .Решение. 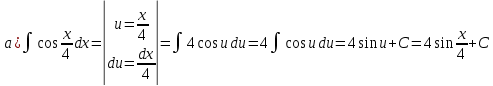 б) 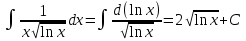 . .в) 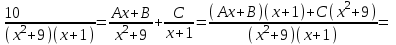 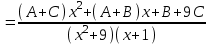 ; ; 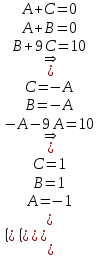 ; ;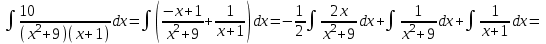 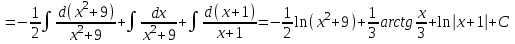 . .г) 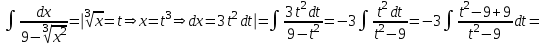 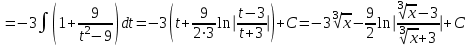 . .д) 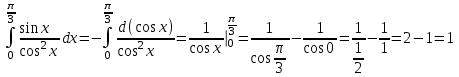 . .e) 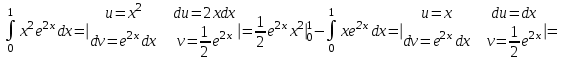 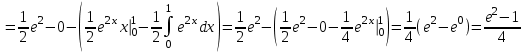 . .Задание №158 вычислить несобственный интеграл или доказать его расходимость 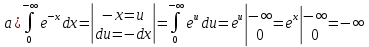 Интеграл расходится на верхнем пределе б) 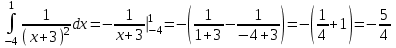 .э= .э=Задание №168 В пункте а) вычислить площадь фигуры, ограниченной графиками заданных функций; в пункте б) вычислить площадь S криволинейной трапеции, ограниченной сверху графиком заданной на отрезке [a,b] функции, длину L кривой, являющейся графиком этой функции, а также объем V тела, ограниченного плоскостью x=b и поверхностью, образованной вращением вокруг оси ОХ графика заданной функции. а) 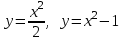 ; б) ; б) 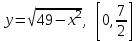 . .Решение. а) Найдем точки пересечения графиков функции из системы: 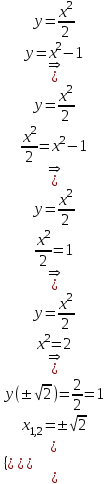 . . 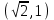 и и 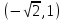 - точки пересечения парабол. - точки пересечения парабол.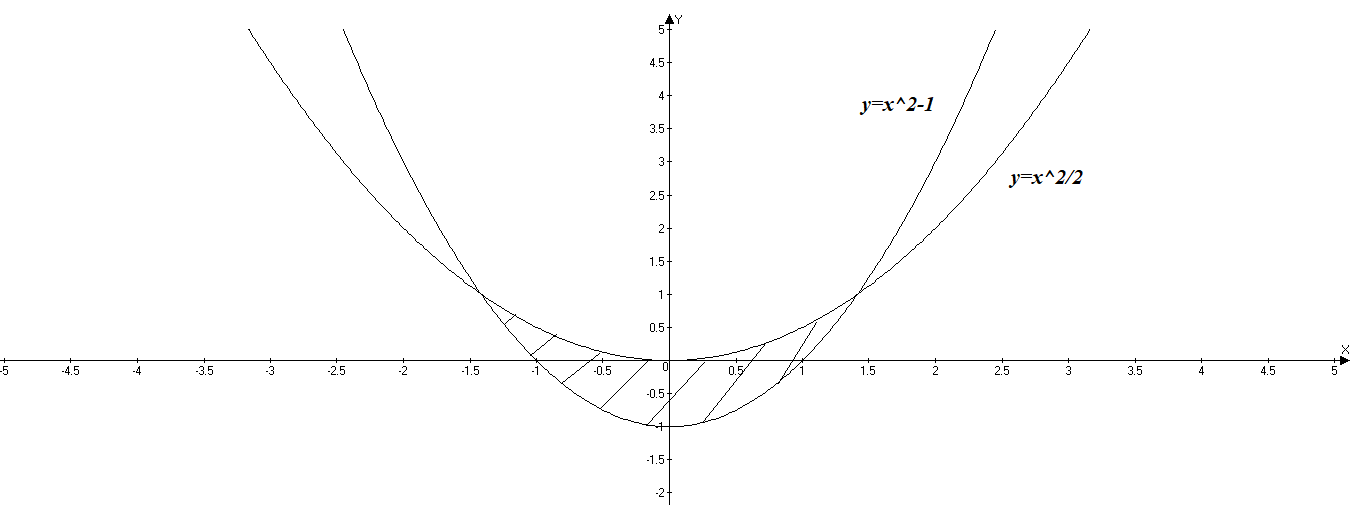 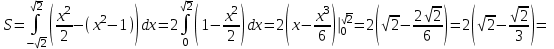 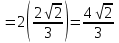 (кв.ед.). (кв.ед.).б) 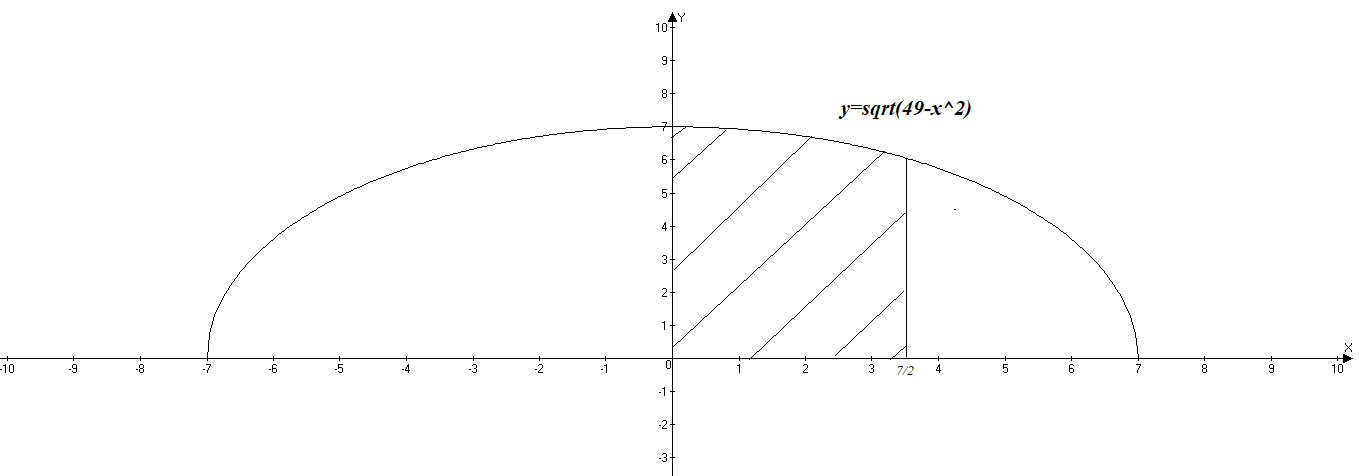 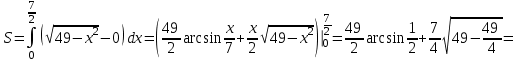 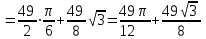 (кв.ед.). (кв.ед.).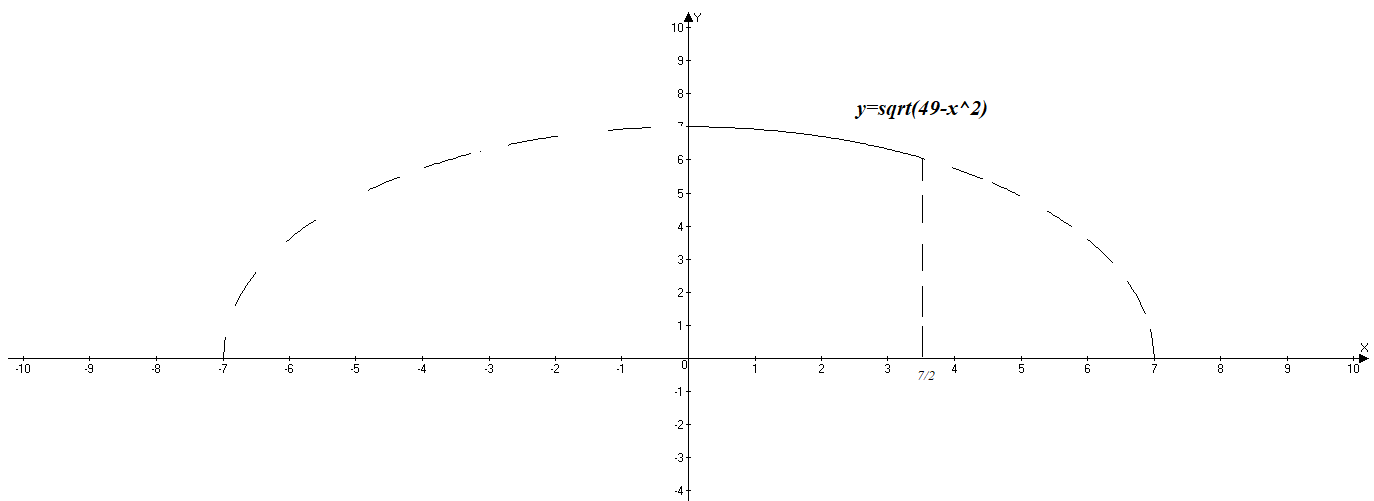 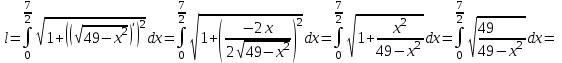 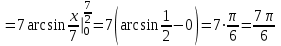 (ед.). (ед.).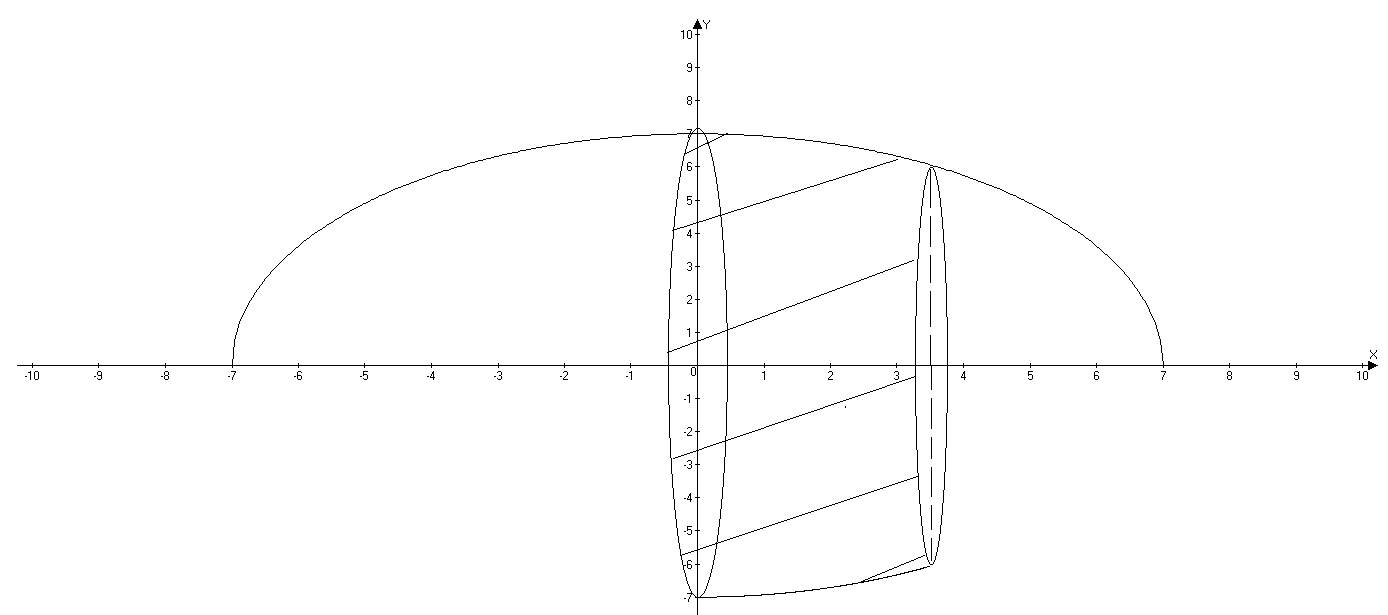 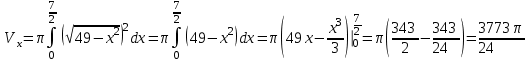 (куб.ед.). (куб.ед.). |
