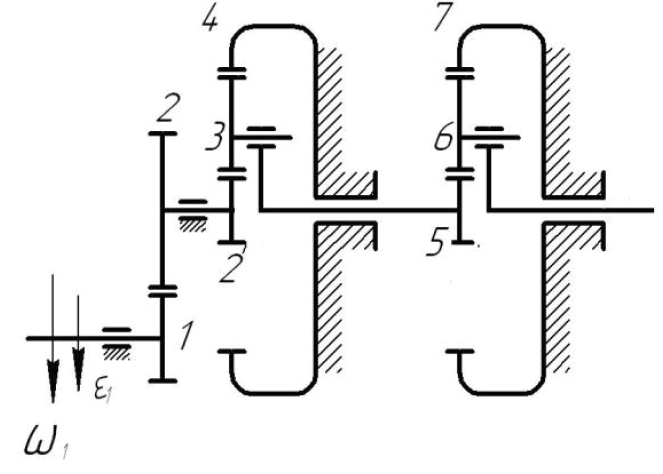
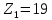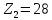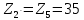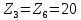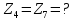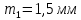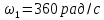Задание Аналитическим методом определить передаточное отношение и степень подвижности многоступенчатого зубчатого механизма. Не достающее значение количества зубьев планетарного механизма найти из условия соосности. Исходные данные
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯРОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Тольяттинский государственный университет» (наименование института полностью) Кафедра /департамент /центр __________________________________________________ (наименование кафедры/департамента/центра полностью) (код и наименование направления подготовки, специальности) (направленность (профиль) / специализация) Практическое задание № 3  по учебному курсу « Механика 3 » по учебному курсу « Механика 3 »(наименование учебного курса) Вариант 12
Тольятти 2023 Задание 3Задание Аналитическим методом определить передаточное отношение и степень подвижности многоступенчатого зубчатого механизма. Не достающее значение количества зубьев планетарного механизма найти из условия соосности. Исходные данные
Решение. Степень подвижности данного механизма определяется по формуле Чебышева: 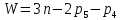 , ,где 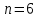 – число подвижных звеньев механизма (1, 2-2', 3, – число подвижных звеньев механизма (1, 2-2', 3, 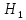 -5, 6, -5, 6, 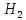 ); );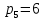 – количество одноподвижных кинематических пар 5 класса (0-1, 0-2(2'), – количество одноподвижных кинематических пар 5 класса (0-1, 0-2(2'), 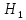 -3, 0- -3, 0-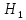 (5), (5), 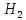 -6, 0- -6, 0-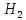 ); );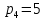 – количество двухподвижных кинематических пар 4 класса (1-2, 2'-3, 3-4, 5-6, 6-7). – количество двухподвижных кинематических пар 4 класса (1-2, 2'-3, 3-4, 5-6, 6-7).Стойка – неподвижное звено, всегда имеет обозначение 0. 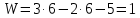 . .Рассчитаем, исходя из условия соосности, недостающее количество зубьев у колеса 4. Условие соосности заключается в том, чтобы геометрические оси ведущего и ведомого валов совпадали.Составим условия соосности: 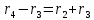 . .Так как 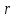 – радиус делительной окружности равен – радиус делительной окружности равен 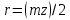 , а модуль колес , а модуль колес 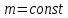 , то есть одинаковый для всех звеньев механизма, то можно утверждать, что радиус колеса равен числу зубьев , то есть одинаковый для всех звеньев механизма, то можно утверждать, что радиус колеса равен числу зубьев 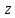 этого же колеса и можно записать условие соосности через числа зубьев колес: этого же колеса и можно записать условие соосности через числа зубьев колес: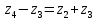 . .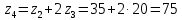 . .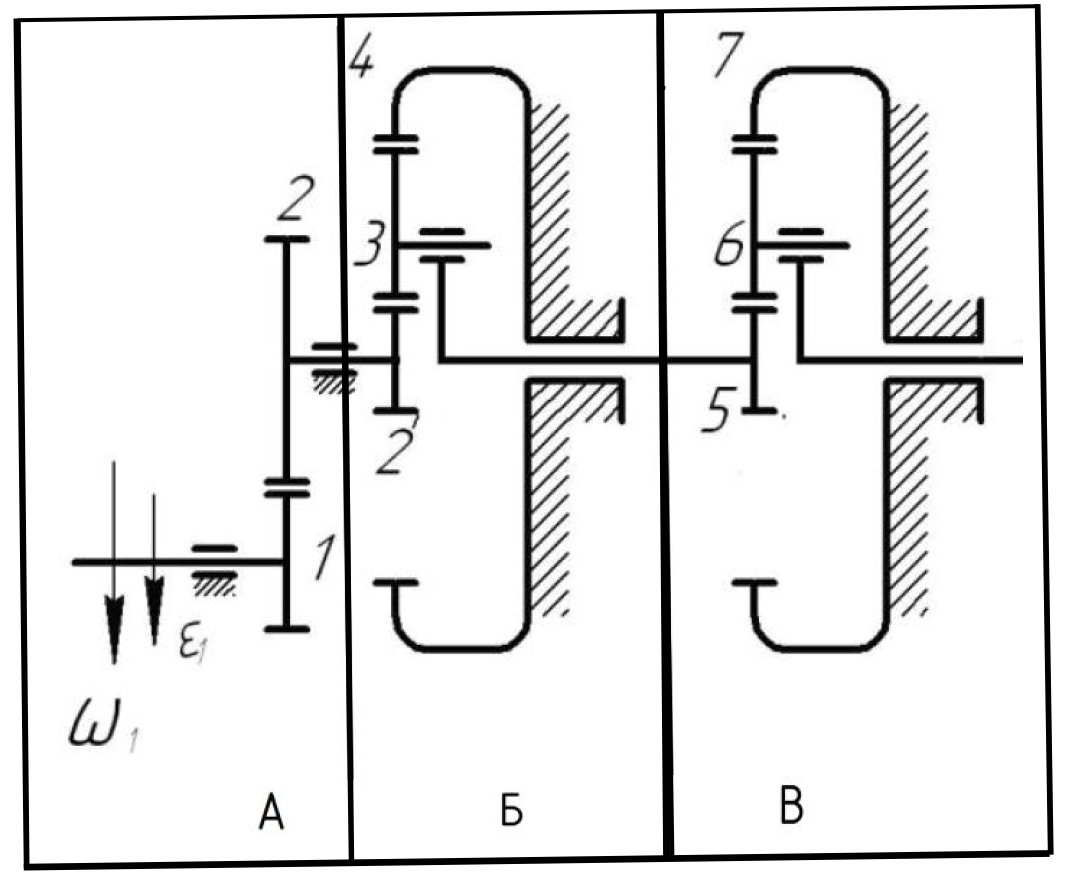 Рис. 1 В заданном многоступенчатом редукторе можно выделить три ступени (Рис. 1): А – простая ступень, Б и В – планетарные ступени. Полное передаточное отношение редуктора будет равно произведению передаточных отношений ступеней, входящих в редуктор. Для схемы редуктора на рис. 1 полное передаточное отношение определяется по формуле: 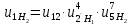 . .Передаточное отношение ступени А, состоящей из зубчатых колес 1 и 2, определяется по формуле: 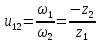 , , подставив значения, получим: 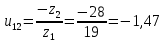 . . Передаточное отношение планетарного механизма (ступень Б) получаем из формулы Виллиса для планетарного механизма: 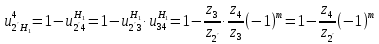 , ,где m – количество внешних зацеплений. 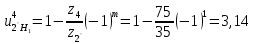 . .Аналогично определяем передаточное отношение ступени В: 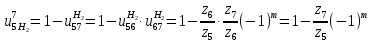 , ,где m – количество внешних зацеплений. 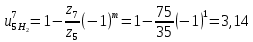 . .Передаточное отношение всего механизма: 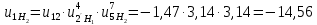 . . |