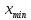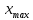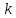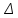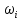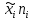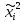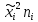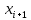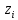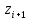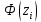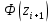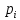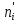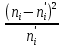Задание Для следующих данных
 Скачать 41.78 Kb. Скачать 41.78 Kb.
|
|
Расчётная работа №1 «Оценки параметров нормального закона распределения» Вариант 13 Задание: Для следующих данных: Составить интервальную таблицу частот, относительных частот и их плотностей. Построить гистограмму частот и аппроксимировать гистограмму теоретическим нормальным законом распределения. Рассчитать выборочные характеристики 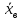 , , 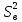 , , 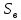 . .С помощью критерия 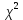 (критерия Пирсона) проверить согласованность теоретического и статистического законов распределений с надежностью (критерия Пирсона) проверить согласованность теоретического и статистического законов распределений с надежностью 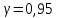 . .Получить точечные оценки для математического ожидания, дисперсии, среднего квадратического отклонения. С надежностью 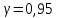 найти доверительный интервал для математического ожидания и среднего квадратического отклонения. найти доверительный интервал для математического ожидания и среднего квадратического отклонения.Среднее число обрывов пряжи 20 текс (хлопок с лавсаном) на сновальной машине на 1 млн. м одиночной нити:
Выполнение работы. Составить интервальную таблицу частот, относительных частот и их плотностей. Расположим все числа в порядке возрастания.
Составим интервальный статистический ряд, для этого: Найдем 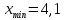 , , 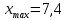 , размах: , размах: 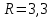 и количество частичных интервалов по формуле Стерджесса ( и количество частичных интервалов по формуле Стерджесса ( ): ):  Далее найдем длину частичного интервала: 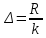 Где 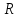 подберем такой, чтобы он нацело делился на k (R = 3,5). И соответственно изменим границы. Получатся следующие данные подберем такой, чтобы он нацело делился на k (R = 3,5). И соответственно изменим границы. Получатся следующие данные
Затем найдем для каждого рядя найдем количество значений (частоту) 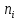 , относительную частоту , относительную частоту 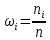 , плотность относительной частоты , плотность относительной частоты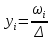 . .
Построить гистограмму частот и аппроксимировать гистограмму теоретическим нормальным законом распределения.  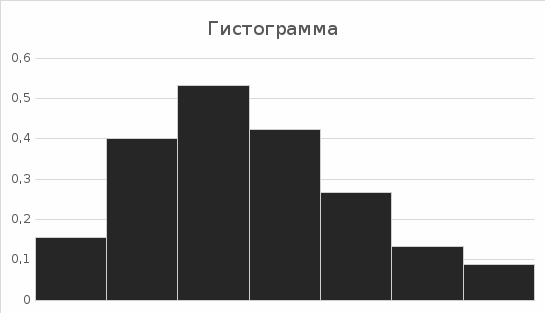  По виду гистограммы плотности относительной частоты можно судить, что с.в. X имеет нормальное распределение. Рассчитать выборочные характеристики 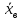 , , 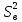 , , 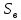 . .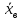 – Cреднее арифметическое всех значений выборки. – Cреднее арифметическое всех значений выборки.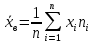 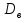 – Выборочная дисперсия. – Выборочная дисперсия.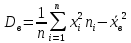 Так как мы используем интервалы, вместо 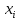 будем использовать будем использовать 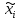 (середина интервала). (середина интервала).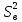 – исправленная выборочная дисперсия. – исправленная выборочная дисперсия. 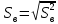 – исправленное среднее квадратическое отклонение. – исправленное среднее квадратическое отклонение.Для этих данных построим соответствующую таблицу.
Получим следующие данные
С помощью критерия 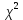 (критерия Пирсона) проверить согласованность теоретического и статистического законов распределений с надежностью (критерия Пирсона) проверить согласованность теоретического и статистического законов распределений с надежностью 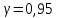 . .Для этого найдем: 1) 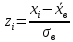  Где 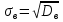 , , 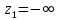 , а , а  . .2) 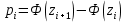 Где 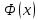 – интегральная функция Муавра-Лапласа. – интегральная функция Муавра-Лапласа.3) Находим теоретические частоты 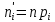 4) Найдем наблюдаем критерий пирсона 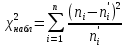 Построим таблицу для этих данных.
Отсюда 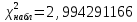 . Далее по таблице критических точек распределения находим . Далее по таблице критических точек распределения находим 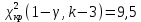 . .Так как 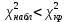 , то теоретический и статистический законы распределения согласованны. , то теоретический и статистический законы распределения согласованны.Получить точечные оценки для математического ожидания, дисперсии, среднего квадратического отклонения. Несмещенной точечной оценкой математического ожидания служит выборочная средняя 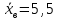 . .Несмещенной точечной оценкой дисперсии является «исправленная дисперсия» 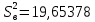 . .Несмещенной точечной оценкой среднего квадратического отклонения является исправленное среднее квадратическое отклонение 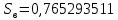 . .С надежностью 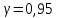 найти доверительный интервал для математического ожидания и среднего квадратического отклонения. найти доверительный интервал для математического ожидания и среднего квадратического отклонения.Для математического ожидания: Т.к. 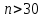 и нам известно и нам известно 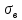 , то формула доверительного интервала примет следующий вид. , то формула доверительного интервала примет следующий вид.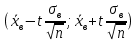 , где , где 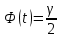 Найдем t. 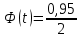 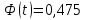 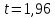 Тогда доверительный интервал примет вид: 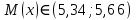 Для среднего квадратического отклонения: Сначала необходимо найти ближайшее значение 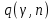 по таблице. по таблице.Для наших данных 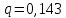 . .При 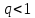 : :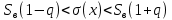 Получаем: 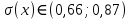 |