Задание Изобразить на плоскости график кусочнолинейной функции Подобрать параметр так, чтобы функция была непрерывной. Порядок решения
 Скачать 230.5 Kb.
|
|
Задание 2. Изобразить на плоскости график кусочно-линейной функции:  Подобрать параметр  так, чтобы функция была непрерывной.Порядок решения: График рассматриваемой функции состоит из двух ветвей. Первая ветвь совпадает с графиком линейной функцией  на отрезке  . Вторая ветвь графика (в области  ) продиктована линейной функцией  и легко будет построена, как только будет определено число . Чтобы график функции  был непрерывным при всех , число следует выбрать так, чтобы две ветви графика «соединились» при  . Значит, значения функций  и  при  должны совпадать. Отсюда находим:  .Построим часть графика 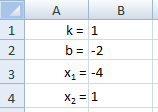. Для этого введем в диапазон ячеек, например, B1:B4 рабочего листа Excel данные в задании коэффициенты  и  , начальную и конечную точки промежутка рассмотрения функции, которые обозначим  ,  . В ячейках A1:A4 дадим текстовые пояснения введенных начальных данных задачи (рис. 1). Рис. 1 Начальные данные для построения графика функции Вычислим таблицу значений функции при  и . Для этого в ячейки B6:B7 вводим формулу вычисления  и  через значения  ,  , перенесенные из ячеек B3:B4 в A6:A7 соответственно (рис. 2). Рис. 2 Расчет значений функции и Выделим левой клавишей мыши числовой диапазон ячеек A6:B7. Зададим последовательно команды выбора в меню: Вставка → Диаграммы → Точечные →Точечная с прямыми отрезками и маркерами. Выполним переименование названия подписей в полученной диаграмме. В первую очередь правильно расположим в диаграмме координатные оси, чтобы горизонтальная являлась осью  – значений аргумента, а вертикальная –  ,значений функции. Также введем, при необходимости, подписи и комментарии к диаграмме. Для этого выделим диаграмму с графиком, поставив курсор на любое свободное (не занятое ни графиком, ни сеткой) место на диаграмме, затем щелкнув правой кнопкой мыши, выбираем из контекстного меню команду «Выбрать данные». В результате этих действий получим диалоговое окно, в котором можем поменять местами координатные оси в случае их неправильного расположения (одним щелчком по левой кнопке мыши, предварительно поставив курсор на панель «Строка/столбец» в центре окна), выбирать для изменения, ввода или удаления различные данные (работая с левой половиной диалогового окна «Элементы легенды/ряды») (рис. 3). 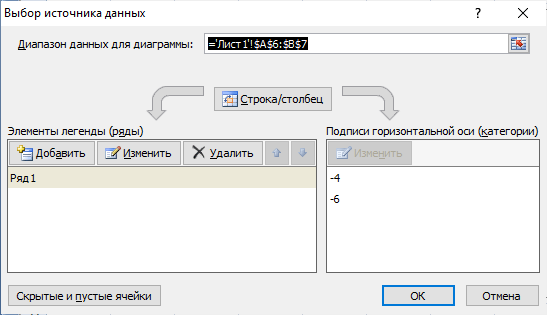 Рис. 3 Диалоговое окно «Выбор источника данных» Итак, получаем график функции 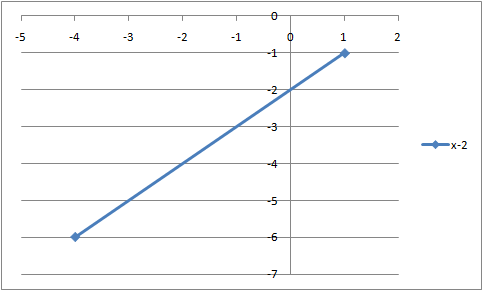на отрезке (рис. 4). Рис. 4 График функции на отрезке Построим часть графика . Для этого введем в диапазон ячеек, например, D1:D4 рабочего листа Excel данные в задании коэффициенты и  , начальную и конечную точки промежутка рассмотрения функции, которые обозначим  ,  . В ячейках C1:C4 дадим текстовые пояснения введенных начальных данных задачи (рис. 5). Рис. 5 Начальные данные для построения графика функции Вычислим таблицу значений функции при 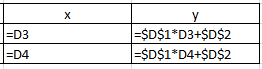 и . Для этого в ячейки D6:D7 вводим формулу вычисления  и  через значения , , перенесенные из ячеек D3:D4 в C6:C7 соответственно (рис. 6). Рис. 6 Расчет значений функции и Выделим диаграмму с графиком, поставив курсор на любое свободное (не занятое ни графиком, ни сеткой) место на диаграмме, затем щелкнув правой кнопкой мыши, выбираем из контекстного меню команду «Выбрать данные». В результате этих действий получим диалоговое окно «Выбор источника данных». В поле «Элементы легенды (ряды)» нажимаем на кнопку «Добавить» и в появившемся диалоговом окне вводим: имя ряда: a*x+1; Значения X: =Лист1!$C$6:$C$7; Значения Y:=Лист1!$D$6:$D$7. Указанные диапазоны ячеек просто выбираем мышкой. Итак, получаем график исходной функции с подобранным параметром на отрезке 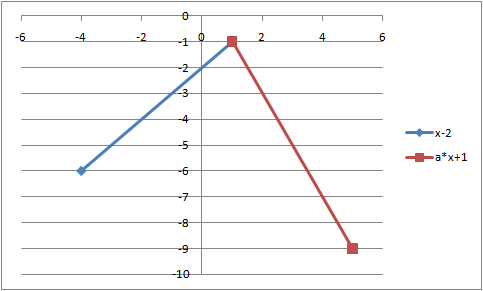 (рис. 7). Рис. 7 График функции на отрезке |