Задание на контрольную работу. I. Механика электропривода

• Название: Задание на контрольную работу. I. Механика электропривода
• Дата: 11.02.2022
• Размер: 1.34 Mb.
• Имя файла: privod_kontr_rab_1_9928851.doc
• Тип: Документы; #358027
• страница: 2 из 6

Основное уравнение движения электропривода.

При переменных статических моментах и моментах инерции, зависящих от скорости, времени, угла поворота вала двигателя (линейного перемещения РО), уравнение движения электропривода записывается в общем виде:



При постоянном моменте инерции уравнение упрощается:



Правую часть уравнения называют динамическим моментом. Знак определяет знак производной и состояние электропривода:

− двигатель разгоняется;

− двигатель снижает скорость;

− установившийся режим работы двигателя, его скорость неизменна.

Темп разгона зависит от момента инерции электропривода, определяющего способность механической части электропривода запасать кинетическую энергию.

Для анализа режимов работы и решения задач удобнее записать основное уравнение движения в относительных единицах (о.е.). Приняв за базовые значения момента − номинальный электромагнитный момент двигателя, скорости − скорость идеального холостого хода при номинальном напряжении на якоре и номинальном токе возбуждения, основное уравнение движения в о.е. записывается в виде:

,

где − механическая постоянная времени электропривода, Учитывающая и приведенный момент инерции РО. Наличие в уравнении свидетельствует о записи уравнения в о.е.
Пример 2.

Рассчитать для механизма с двигателем ( кВт; рад/с; В; А) и суммарным моментом инерции кг·м² динамический момент , ускорение электропривода , конечное значение скорости , угол поворота вала двигателя за промежуток времени , если , , .
Основное уравнения движения в о.е.



Механическая постоянная времени двигателя



Значения и рассчитаем по каталожным данным двигателя.

Скорость идеального холостого хода:

рад/с

Номинальный электромагнитный момент:

Н·м

Механическая постоянная времени:

с

Динамический момент:



Ускорение электропривода (при )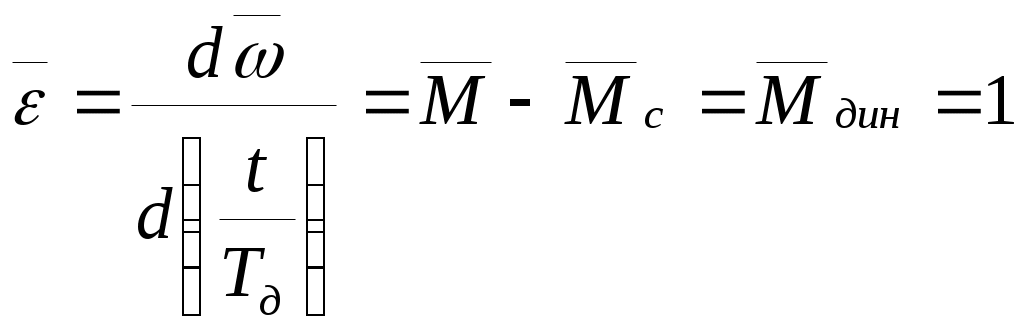



Приращение скорости за промежуток времени



Конечное значение скорости на участке:



Приращение угла поворота:



Определим полученные значения абсолютных единицах:

Н·м

рад/с²

рад/с

рад/с

рад

Расчет характеристик, параметров схемы включения и переходных процессов двигателя постоянного тока независимого возбуждения.
Напряжение U, приложенное к якорной цепи двигателя постоянного тока, уравновешивается ЭДС двигателя и падением напряжения в сопротивлениях якорной цепи от протекающего тока якоря I.



где , В;

R – сопротивление якорной цепи, Ом;

L – индуктивность якорной цепи, Гн;

Ф – магнитный поток двигателя, Вб;

– конструктивный коэффициент, учитывающий число пар полюсов , число активных проводников N и число параллельных ветвей а якорной обмотки.

Для установившегося режима уравнение примет вид:

,

при этом для двигателя постоянного тока с независимым возбуждением поток Ф постоянен, а в двигателях последовательного и смешанного возбуждения поток Ф зависит от тока якоря.

Выражение механической характеристики двигателя постоянного тока имеет вид:

,

где − электромагнитный момент двигателя, Н·м.

Естественной называют механическую характеристику двигателя при номинальном напряжении питающей сети и отсутствии добавочных сопротивлений в цепях двигателя (для двигателя с независимым возбуждением − при номинальном потоке ).

Принимая за базовые величины , , , а также , , , выражение механической характеристики в общем виде записывают в о.е.

(*)

Естественная механическая характеристика двигателя постоянного тока с независимым возбуждением ( , , − невыключаемое сопротивление) в о.е. имеет вид:



При естественная механическая характеристика двигателя постоянного тока с независимым возбуждением записывается в виде, удобном для построения:



Если , то .

Если , то , а

Таким образом, естественная механическая характеристика двигателя постоянного тока с независимым возбуждением строится по двум точкам.

По двум точкам строятся и искусственные механические характеристики, только используется формула (*), и изменяются в зависимости от изменяемого параметра схемы включения:

;

Пример 3.

Для двигателя постоянного тока ( кВт, В, А, рад/с, кг·м²) рассчитать и построить естественную механическую и естественную электромеханическую характеристики.
Для построения механической и электромеханической характеристик необходимо рассчитать координаты двух точек: идеального холостого хода и номинальной скорости , причем под следует понимать электромагнитный номинальный момент , который отличается от момента на валу на величину потерь холостого хода:



Скорость идеального холостого хода при номинальном потоке:



где − номинальный коэффициент ЭДС Е двигателя.



Если сопротивление цепи якоря не приведено в каталоге, его можно рассчитать приближенно из условия примерного равенства постоянных и переменных потерь в номинальном режиме работы двигателя.

Ом

Тогда

, В·с

Скорость идеального холостого хода:

рад/с

Номинальный электромагнитный момент:

Н·м

Выбираем базовые величины

В

А

В·с

рад/с

Н·м

Ом

Пример 4.

Для двигателя постоянного тока ( кВт, В, А, рад/с, кг·м²) рассчитать и построить правильную пусковую диаграмму, обеспечивающую пуск двигателя за минимальное время при и . Принять число ступеней .
Для обеспечения минимального времени переходного процесса двигатель должен работать с предельным моментом , ограниченным условиями коммутации тока якоря. Для предложенного двигателя Н·м (величина для каждого типа двигателя приводится в каталогах как , при отсутствии каталога принимают ).

Максимальный момент пусковой диаграммы:



Определим момент переключения пусковой диаграммы





Рассчитаем полные сопротивления якорной цепи:

Ом

Ом

Ом

Проверим правильность расчета:

Ом

Величины ступеней сопротивлений:

Ом

Ом

Ом

Максимальный ток пусковой диаграммы:

А

Ток переключения правильной пусковой диаграммы: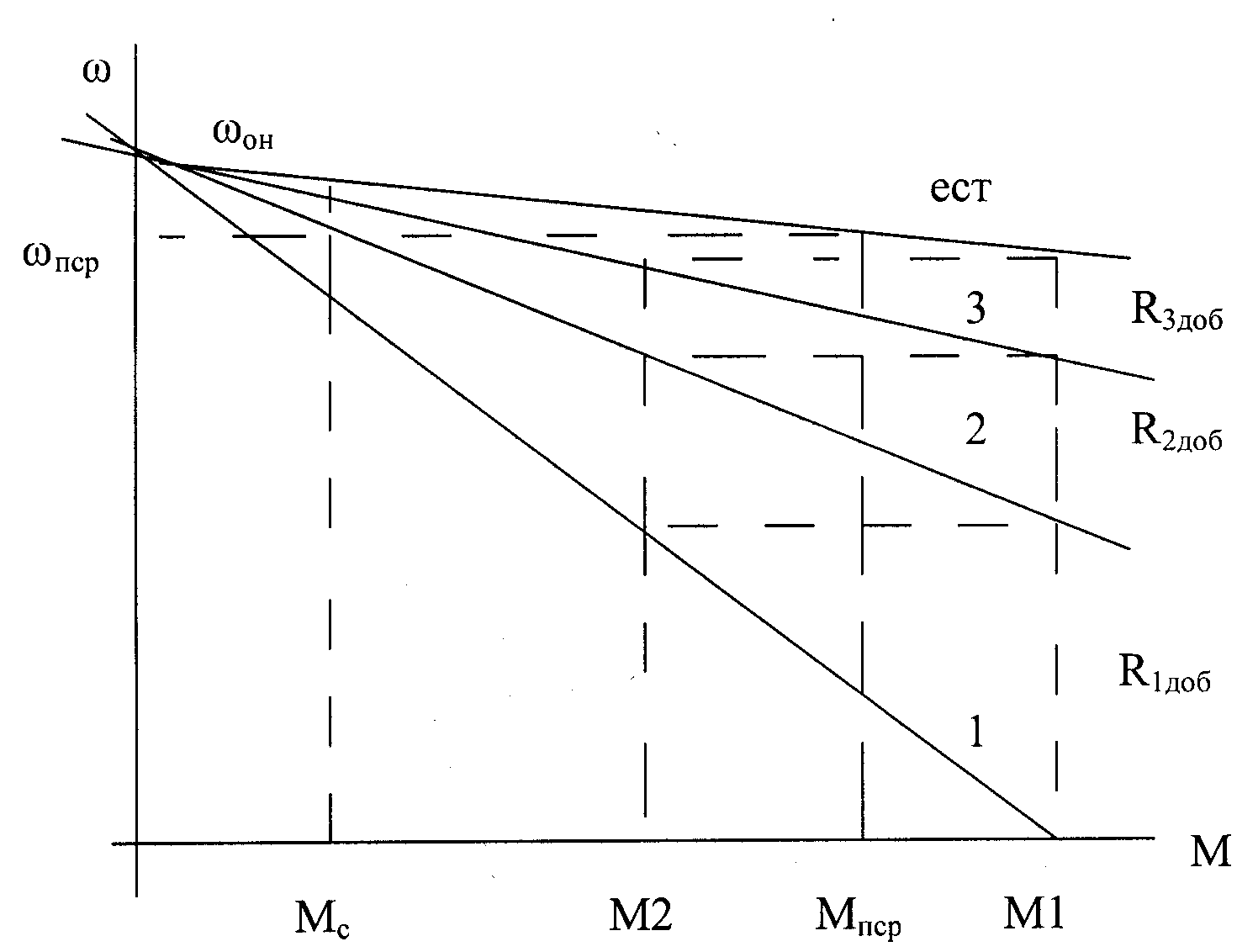

А