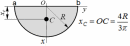
Статика. Задача С2 Определение координат центра тяжести тела. Задание на контрольную работу
 Скачать 197.59 Kb. Скачать 197.59 Kb.
|
|
ЗАДАНИЕ на контрольную работу Выполнение контрольной работы требует решения ряда заданий по всем разделам курса теоретической механики. Каждое из заданий представляет собой индивидуальную задачу. СТАТИКА Две однородные прямоугольные пластины, приваренные под прямым углом друг к другу, образуют угольник. Размеры пластин в направлениях, параллельных координатным осям х, у, z, равны соответственно или  , ,  и и 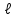 (рис.С2.0÷С2.4), или (рис.С2.0÷С2.4), или  , ,  и и 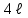 (рис. С2.5÷С2.9). Силы тяжести большей и меньшей пластин (рис. С2.0÷С2.4) соответственно равны 10 кН и 4 кН, для рис. С2.5÷ С2.9 силы тяжести пластин одинаковы и равны 8 кН. Каждая из пластин расположена параллельно одной из координатных плоскостей (плоскость хАу горизонтальная). (рис. С2.5÷С2.9). Силы тяжести большей и меньшей пластин (рис. С2.0÷С2.4) соответственно равны 10 кН и 4 кН, для рис. С2.5÷ С2.9 силы тяжести пластин одинаковы и равны 8 кН. Каждая из пластин расположена параллельно одной из координатных плоскостей (плоскость хАу горизонтальная).Из одной из пластин угольника вырезана фигура, расположение и вид которой указаны в таблице С2. Точки, обозначенные на рисунках, находятся по краям или в серединах сторон пластин. Вычислить координаты центра тяжести угольника с вырезом для указанных на рисунках систем координат. При расчетах принять 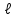 = 0,5 м. Толщиной пластин пренебречь. = 0,5 м. Толщиной пластин пренебречь.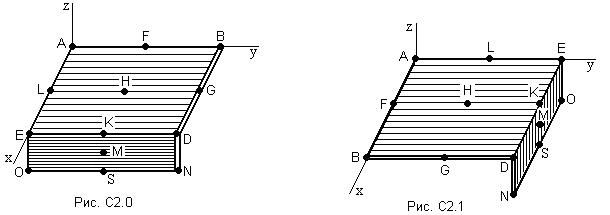 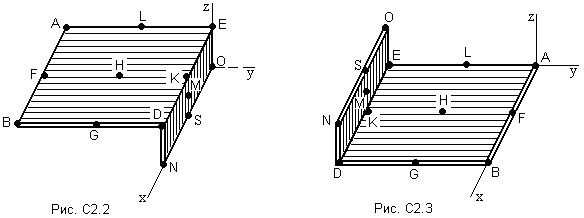 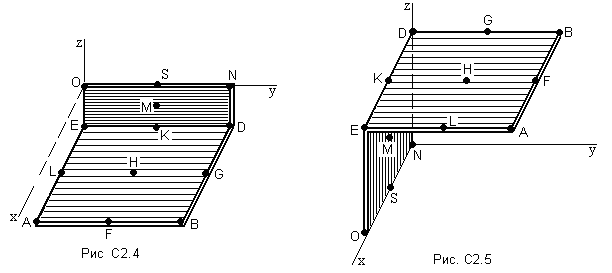 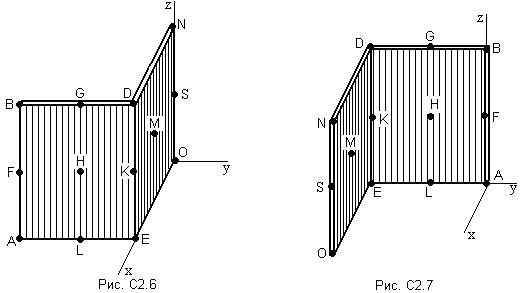 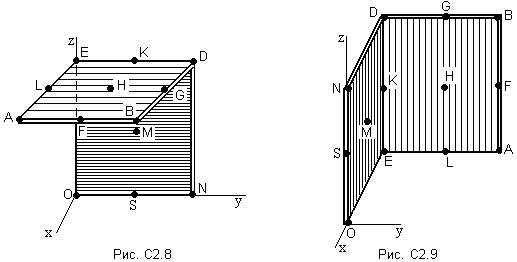 Таблица С2 Расположение и вид вырезаемой фигуры
Указания. Решение задач на определение центра тяжести плоской фигуры рекомендуется проводить в следующем порядке: – исследуемую конструкцию разбить на части, для которых положение центра тяжести известно или его можно легко определить, например, на простейшие геометрические фигуры, при этом считать, что вырезанные из конструкции части (фигуры) обладают отрицательной площадью; – определить площади частей конструкции; – найти координаты центров тяжести частей конструкции в выбранной системе координат; – найденные значения подставить в формулы: 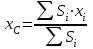 , , 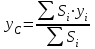 , , 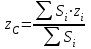 , ,где Si – площади частей конструкции, хi, уi, zi – координаты центра тяжести частей конструкции, и произвести вычисления. Пример решения задачи С2 Д 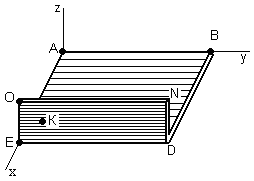 ве однородные прямоугольные пластины, приваренные под прямым углом друг к другу, образуют угольник. Размеры пластин в направлениях, параллельных координатным осям х, у, z, равны соответственно ве однородные прямоугольные пластины, приваренные под прямым углом друг к другу, образуют угольник. Размеры пластин в направлениях, параллельных координатным осям х, у, z, равны соответственно  , ,  и и  . Вес большей из пластин равен G1 = 5 кН, вес меньшей – G2 = 2,5 кН. Каждая из пластин расположена параллельно одной из координатных плоскостей (плоскость хАу является горизонтальной). . Вес большей из пластин равен G1 = 5 кН, вес меньшей – G2 = 2,5 кН. Каждая из пластин расположена параллельно одной из координатных плоскостей (плоскость хАу является горизонтальной).Из угольника вырезана фигура в виде прямоугольного треугольника, расположение которого обозначено буквами ЕОК (гипотенуза совпадает с прямой ЕО). Вычислить координаты центра тяжести пространственной фигуры в виде угольника с вырезом для обозначенной на рисунке системы координат. При расчетах принять расстояние ℓ равным0,5 м. Толщиной пластин пренебречь. Решение Сделаем рисунок изучаемой конструкции с вырезом в меньшей плите. 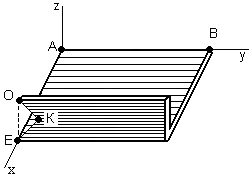 Для решения задачи целесообразно применить или метод разбиения тела на части, или разновидность этого метода - метод отрицательных площадей, для чего использовать формулы 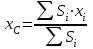 , , 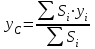 , , 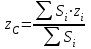 , ,где Si – площади частей однородной конструкции, хi , уi , zi – координаты центра тяжести частей конструкции. Разобьем конструкцию на три части - большая пластина, меньшая пластина и вырезанный треугольник, который будем считать телом с отрицательной площадью. Центры тяжести большей С1 и меньшей С2 пластин в виде прямоугольников находятся на пересечении диагоналей, а центр тяжести С3 выреза в виде треугольника находится на пересечении медиан. Точки С1, С2 и С3 покажем на рисунке. 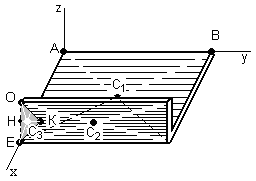 Координаты центров тяжести частей конструкции С1, С2 и С3 для указанной на рисунке системы координат соответственно равны: 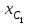 = = 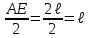 , , 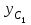 = = 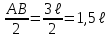 , , 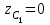 ; ;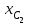 = = 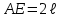 , , 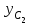 = = 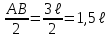 , , 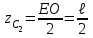 ; ;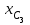 = = 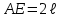 , , 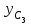 = = 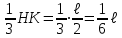 , , 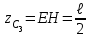 . .Найдем площади каждой из пластин и вырезаемого треугольника: − большая пластина S1 = 2ℓ · 3ℓ = 6ℓ2; − меньшая пластина S2 = ℓ · 3ℓ = 3ℓ2; − треугольник S3 = 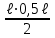 = 0,25ℓ2. = 0,25ℓ2.Используя метод отрицательных площадей, определим координаты центра тяжести С всей конструкции: 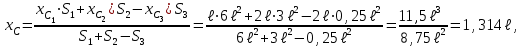 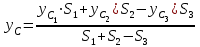 = =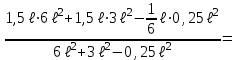 = 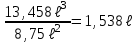 , ,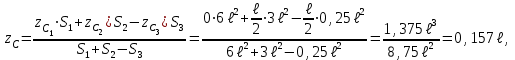 где S1, S2, S3 – площади соответственно большей и меньшей пластин, а также выреза в виде треугольника. Подставляя в формулы заданное значение 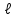 = 0,5 м, вычислим координаты центра тяжести всей конструкции: = 0,5 м, вычислим координаты центра тяжести всей конструкции: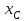 = 0,657 м, = 0,657 м, 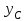 = 0,769 м, = 0,769 м, 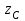 = 0,0785 м. = 0,0785 м.Ответ: координаты центра тяжести конструкции соответственно равны: 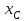 = 0,657 м, = 0,657 м, 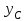 = 0,769 м, = 0,769 м, 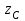 = 0,0785 м. = 0,0785 м. | |||||||||||||||||||||||||||||||||||||||||||||||||||||