Курсовая ОТУ. Задание на курсовую работу по дисциплине организация транспортных услуг и безопасность транспортных процессов Студенткагр
 Скачать 312.55 Kb. Скачать 312.55 Kb.
|
|
ЗАДАНИЕ на курсовую работу по дисциплине «ОРГАНИЗАЦИЯ ТРАНСПОРТНЫХ УСЛУГ И БЕЗОПАСНОСТЬ ТРАНСПОРТНЫХ ПРОЦЕССОВ» Студенткагр
Задание 1 В таблице приведены данные об изменении некоторого показателя за последние годы. Сделать прогноз изменения того же показателя на ближайшие три года. Рассмотреть два варианта: 1)Считать значения всех наблюдений одинаковыми; 2)Весомость каждого предыдущего наблюдения считать равной 0,8 от последующего. Задание 2 Имеются схем городского района с указанием количества потенциальных пассажиров воздушного транспорта рисунок 1, и количества пассажиров, пользующихся кассой агентства воздушных сообщений рисунок 2. Определить оптимальное расположение кассы и количество пассажиров, пользующихся кассой, при этом расположении. Считать кварталы квадратами с длиной стороны 1 км. Число пассажиров на рисунках указаны в тысячах человек. Исходное положение кассы в центре нижнего левого квартала.
Рисунок 2. Количество
РЕФЕРАТ Пояснительная записка:23с., 4 рисунка, 4 таблицы, 2 источника. ПРОДАЖА ВОЗДУШНЫХ ПЕРЕВОЗОК, ПРОГНОЗИРОВАНИЕ, ЛИНЕЙНАЯ РЕГРЕССИЯ, ОПТИМИЗАЦИЯ, ГРАВИТАЦИОННАЯ МОДЕЛЬ. Курсовой проект состоит из двух разделов. В каждом из них необходимо решить задачу по оптимизации рабочего процесса. В первом разделе предлагается сделать прогноз на то, как будит изменятся некая величина Y на протяжении последующих трех лет. В качестве исходных данных нам дается ее изменении за последние 15 лет. Во втором разделе предлагается оценить эффективность работы кассы по продаже авиабилетов и определить ее наиболее выгодное месторасположения. В качестве исходных данных нам дается схема расположения кварталов жилого района с количеством клиентов, пользующихся услугами данной кассы, и общим количеством жителей в каждом квартале. СОДЕРЖАНИЕ ВВЕДЕНИЕ………………………………………………………………….6 1 ЗАДАЧИ ПРОГНОЗИРОВАНИЯ В ОРГАНИЗАЦИИ УСЛУГ ВОЗДУШНОГО ТРАНСПОРТА………………………………………….7 Постановка задач прогнозирования……………………………………7 Регрессионные модели прогноза……………………………………….8 Регрессионная модель прогноза при одинаковой значимости наблюдений…………………………………………………………………9 Регрессионная модель прогноза при различной значимости наблюдений…………………………………………………………………11 2ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО РАСПОЛОЖЕНИЯ КАССЫ АГЕНСТВА ПО ПРОДАЖЕ ПЕРЕВОЗОК………………………………15 2.1 Оптимизация расположения кассы по продаже авиаперевозок…….15 2.2 Методика решения задачи по оптимизации расположения кассы по продаже авиаперевозок……………………………………………………15 2.3 Расчет числа пассажиров авиа кассы в ее новом положении……….18 ЗАКЛЮЧЕНИЕ…………………………………………………………….22 СПИСОК ЛИТЕРАТУРЫ…………………………………………………23 ВВЕДЕНИЕ В любой крупной компании есть свой аналитический отдел. Он занимается сбором данных по результатам работы компании и производит анализ для оценки эффективности выбранной политики. В современных условиях аналитическая (планово-аналитическая) служба - наиболее гибкий и динамичный подразделение предприятия, функции и структура которой зависят от специфики самого предприятия, характера бизнеса, кадрового потенциала и др. Здесь нет стандартных решений и методик. При создании аналитической службы можно ориентироваться на опыт зарубежных и отечественных предприятий (компаний). Аналитическая служба - это один из центральных подразделений, который отвечает за подготовку и обоснование основных стратегических решений и отслеживает общую картину бизнеса хозяйствующего субъекта (предприятия, фирмы, организации). Основной целью аналитической службы является разработка концепций, планов, программ развития предприятия на основе анализа и оценки результатов его прошлой и текущей деятельности. 1 ЗАДАЧИ ПРОГНОЗИРОВАНИЯ В ОРГАНИЗАЦИИ УСЛУГ ВОЗДУШНОГО ТРАНСПОРТА Постановка задач прогнозирования. Прогнозирование это научно обоснованное предсказание вероятного развития событий на основании статистических исследований. Оно представляет собой оценку, предвидение будущего развития выбранного объекта исследования. Главной целью прогнозирования является разработка научных предпосылок принятия управленческих решений. От сюда выделяют три основные задачи прогнозирования: во первых это научный анализ сложившейся ситуации, во вторых оценка действий данных тенденций в будущем, и в третьих определение возможных альтернатив. Прогнозы различаются по длительности сроков: краткосрочный это прогноз до 1 года, среднесрочный прогноз на срок от 3 до 5 лет, долгосрочный прогноз на срок от 10 лет и больше. В курсовой работе рассмотрим среднесрочный прогноз, сделанный на три года, с использованием статистических данных за последние 15 лет, согласно таблице 1. Рассмотрим использование моделей линейной регрессии для решения задачи прогнозирования в двух постановках. В первой задаче значимость наблюдений одинакова. Во второй задаче предполагается, что более ранние наблюдения имеют меньшую значимость, как частично устаревшие. Таблица1.1 – зафиксированные значения показателя.  Регрессионные модели прогноза. Пусть имеются зафиксированные значения рассматриваемого показателя Y1, Y2,….Yn в момент времени t1, t2,…tn. Метод, предусматривающий построение модели, в которой значение зависимой переменной Y рассматривается как функция одной или нескольких переменных, например t , называется регрессией. Постулируется следующая зависимость между зависимой и сопутствующей переменными: Y=b0+b1*t+Z, Где b0 и b1 – неизвестные параметры модели; t – известные и не случайные значения сопутствующей переменной; Z – случайная величина, сопутствующая наблюдению. Обычно имеется несколько n реализаций модели, то есть каждому i – му моменту времени соответствуют свои величины Y и Z. По этому Yi=b0+b1*ti+Z i=1,…..,n. Для Z вводится предположение: М(Zi)=0; D(Zi)=Ϭ2; i=1,….,n. По этому M(Yi)=b0+b1*ti; D(Yi)=Ϭ2; i=1,….,n. Таким образом прогноз рассчитывается по формуле: yi=b0+b1*ti, является несмещенной оценкой оценкой истинного математического ожидания прогнозируемой величины. Коэффициенты b0 и b1 подбираются так, чтобы сумма квадратов отклонений наблюдений значений Yi от вычисляемых yi была минимальной: 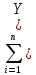 i-(b0+b1*ti))2 i-(b0+b1*ti))2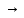 min. min.Данное условие выполняется для b0 и b1, определяемых по формулам: b1= 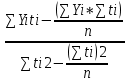 , b0= , b0=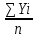 -b1* -b1*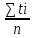 . .В некоторых случаях различным наблюдениям придается различный вес. Более поздние значения рассматриваемого показателя могут оказывать большее влияние на будущее, чем более раннее – частично устаревшие. Будем предавать i- му наблюдению вес Wi. В этом случае 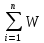 i(Yi-(b0+b1*ti))2 i(Yi-(b0+b1*ti))2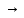 min. min.Формулы преобразуются к виду: b1= 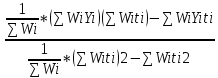 , ,b0= 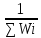 *(∑WiYi-b1∑Witi). *(∑WiYi-b1∑Witi).1.3Регрессионная модель прогноза при одинаковой значимости наблюдений. На основании исходных данных делается прогноз на ближайшие три года при одинаковой значимости наблюдений. Исходные данные и промежуточные результаты расчетов приведены в таблице 1.2. Таблица 1.2 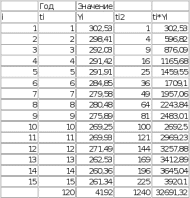 Искомые коэффициенты b0 и b1, определяем по формулам: b1= 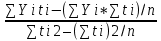 = =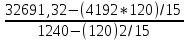 =- =-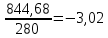 ; ;b0= 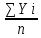 - b1 - b1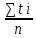 =4192/15 + 3,02*120/15= 303,63. =4192/15 + 3,02*120/15= 303,63.Таким образом, выражение для регрессионной модели прогноза имеет вид: yi =b0+b1ti = 303,63 – 3,02*ti. С использованием данного выражения определяются прогнозируемые значения для: -16-го месяца: y16=b0+b1*t16=303,63 – 3,02*16= 255,31; -17-го месяца: y17=b0+b1*t17=303,63 – 3,02*17= 252,29; -18-го месяца: y18=b0+b1*t18=303,63 – 3,02*18 = 249,27. 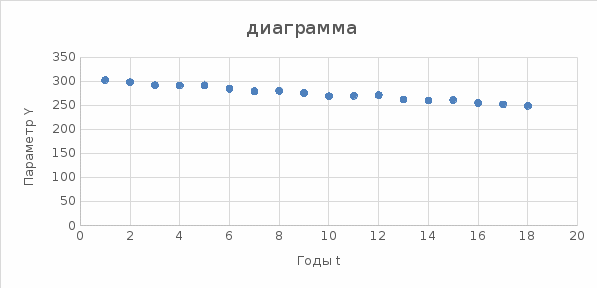 Рисунок 1.1 график изменения показателя у за последние 18 лет. 1.4 Регрессионная модель прогноза при различной значимости наблюдений. На основании исходных данных делается прогноз на ближайшие три месяца при различной значимости наблюдений. Исходные данные и промежуточные расчеты сведены в таблицу 2. В соответствии с заданием весомость каждого предыдущего 0,9 от весомости последующего. Решение оформлено в виде таблицы 1.3. Таблица 1.3. 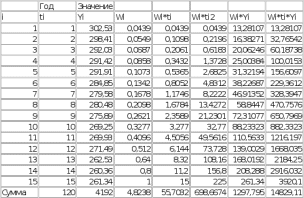 Коэффициенты регрессивной модели определяются по формулам: b1= 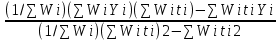 = =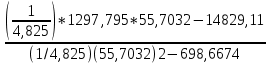 =- =- 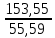 = -2,762. = -2,762.b0= 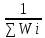 (∑WiYi-b1∑Witi)= (∑WiYi-b1∑Witi)=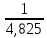 (1297,795+2,762*55,7032)=300,859. (1297,795+2,762*55,7032)=300,859.В данном случае модель для регрессионной модели записывается так: yi=b0+b1ti=300,859-2,762*ti. С использованием данного выражения определяем прогнозное значение для: -16-го месяца: y16=300,859-2,762*16=256,67; -17-го месяца: y17=300,859-2,762*17=253,9; -18-го месяца: y18=300,859-2,762*18=251,14. Расхождение данного прогноза с прогнозом, полученным ранее, объясняется тем, что темпы роста показателя за последние годы несколько увеличился. 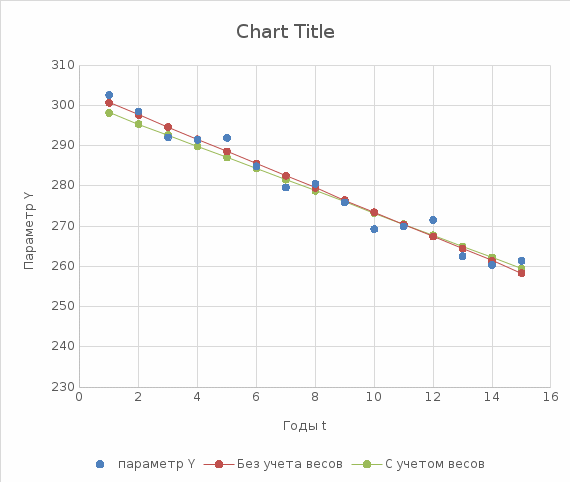 Рисунок 1.2 результаты прогнозирования. 2 ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО РАСПОЛОЖЕНИЯ КАССЫ АГЕНСТВА ПО ПРОДАЖЕ ПЕРЕВОЗОК 2.1 Оптимизация расположения кассы по продаже авиаперевозок. Определение наиболее оптимального места расположения касс по продаже авиаперевозок, одна из наиболее важных и ответственных задач в организации продаж авиабилетов. От этого напрямую зависит успешная работа и прибыль агентства. В моей курсовой работе я проведу анализ жилого района, состоящего из 17 кварталов. Так же нам известно изначальное место расположение кассы, количество жителей в каждом квартале, регулярно пользующихся услугами данной кассой, и количество потенциальных клиентов. Под потенциальными клиентами понимают граждан, проживающих в данном районе и имеющих желание, возможность и потребность в авиаперевозках. Задача состоит в том, чтобы оценить, на сколько эффективно работает касса и будет ли смысл в переносе ее на новое место для привлечения большего количества клиентов. Задача довольно не ординарная так как при переносе на новое место можно не только привлечь новых клиентов, но и потерять старых. Для положительной динамики необходимо что бы привлечение новых пассажиров не только компенсировало потерю старых, а многократно превзошло их. Для этого необходимо произвести математический расчет, и сравнить показатели эффективности работы авиа кассы на старом месте и на новом. 2.2 Методика решения задачи по оптимизации расположения кассы по продаже авиаперевозок. Оптимизация месторасположения кассы по продаже авиа билетов заключается в переносе ее на новое место для привлечения максимально возможного количества клиентов, при наименьших затратах на ее содержание и обслуживание. Для успешного решения данной задачи, требуется комплексное выполнение следующих факторов: - планировка местности; - структура и динамика транспортных сообщений; - учет и разделение на жилые и производственные зоны. На первом этапе поставленной задачи, определим зоны тяготения клиентов к кассам. Смысл в том, что бы они не накладывались друг на друга и не создали конкуренцию. Для описания зон тяготения используется так называемая гравитационная модель, предполагающая, что зона тяготения к кассам описывается некой функцией, убывающей от расстояния. T=f(d), Где T – доля жителей района, удаленного на расстоянии d от кассы, пользующихся ее услугами. Для определения функции тяготения спроса, должны быть известны объемы продаж и данные о численности населения. Функция тяготения может принимать различный вид, но как правило для ее описания применяют квадратичную функцию. T=ad2+bd+c. Где T – доля жителей i – го квартала, пользующихся услугами j – ой кассы, a, b, c – коэффициенты многочлена второй степени. Параметры a, b, c могут быть определены методом наименьших квадратов, однако, получение статистических данных о предпочтении граждан той или иной кассе, занимает очень больших временных и финансовых затрат. По этому, для их определения воспользуемся так называемым косвенным методом, требующим сбора статистических данных значительно меньшего объема. В рамках метода предполагается, что все потенциальные клиенты, находящиеся в близи данной кассы пользуются ее услугами, то есть: при d=0 T=1, а при некотором предельном радиусе: d=D T=0. То есть допускается, что есть такое расстояние, при удалении на которое кассы от жилых районов люди этого района просто перестанут ей пользоваться. Предположим, что на расстоянии d= 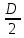 , доля клиентов будит β, тогда: , доля клиентов будит β, тогда:При d= 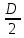 T=β. T=β.Где β это доля жителей, удаленных на расстояние 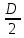 от кассы и пользующиеся ее услугами. Данная величина определяется путем опроса жителей отдаленных от кассы на расстояние от кассы и пользующиеся ее услугами. Данная величина определяется путем опроса жителей отдаленных от кассы на расстояние 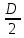 от кассы. от кассы.Необходимые нам коэффициенты a b c найдем следующим образом. Пусть D и β нам заданы. Тогда из условий заданных ранее получим что: с=1 aD2+bD+c=0 a 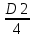 +b +b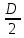 +c=β +c=βрешая полученную систему уравнений получим: a= 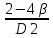 b= b=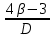 c=1 c=1в результате подстановки полученных выражений в исходное уравнение, оно примет вид: T= 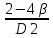 d2+ d2+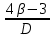 d+1. d+1.В гравитационной модели вводится предположение о том что, количество обслуживаемых пассажиров зависит от расстоянии на которое касса удалена от районов. Так же, предполагая что жители кварталов сосредоточены в их центрах, определим координаты центра масс района. X= 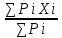 Y= Y=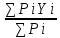 Где Pi – количество потенциальных клиентов i – го квартала, отдающих предпочтение данной кассе. X и Y – это координаты i – го квартала на карте расположения района. 2.3 Расчет числа пассажиров авиа кассы в ее новом положении. Для решения нашей задачи нам понадобятся формулы: X= 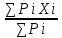 Y= Y=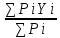 и введем следующие обозначения: и введем следующие обозначения:i – номер квартала Pi – количество потенциальных пассажиров i – го квартала; Piф – фактическое количество клиентов i - го квартала, пользующихся услугами данной кассы; xi yi – координаты расположения i – го квартала на карте местности района. В соответствии с заданием, на рисунке 2.1 изобразим схему нашего района. На которой расположены кварталы, условно принимаем их за квадрат. В их верхней части поставим их нумерацию, а внизу, в виде дроби, количество жителей. В числителе число обозначающее фактическое количество клиентов Piф , а в знаменателе число обозначающее количество потенциальных пассажиров Pi. Исходное расположение кассы обозначим крестиком.
Рисунок 2.1 схема планировки городского района. Преобразуем нашу схему таким образом, чтобы ее можно было разместить на координатной плоскости. Для этого условно представим что жители каждого квартала сосредоточены в центре каждого из кварталов. Таким образом каждому кварталу можно задать координаты x и y , а точку начала координат примем за первоначальное месторасположения кассы. Используя формулы X= 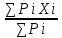 , Y= , Y=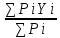 найдем координаты наиболее оптимального расположения кассы по продаже авиабилетов. найдем координаты наиболее оптимального расположения кассы по продаже авиабилетов.X=(4.00*0+6.00*0+3.00*0+3.00*0+2.00*0+2.00*1+5.00*1+8.00*1+6.00*1+6.00*2+5.00*2+4.00*2+3.00*2+2.00*3+2.00*3+2.00*3+4.00*4+1.00*4)/(4+6+3+3+2+2+5+8+6+6+5+4+3+2+2+2+4+1)=1.4 Y=(4*0+6*1+2*1+6*1+3*2+5*2+5*2+2*2+4*2+3*3+8*3+4*3+2*3+2*4+6*4+3*4+2*4+1*4)/(4+6+2+6+3+5+5+2+4+3+8+4+2+2+6+3+2+1)=2,35. Таким образом кассу необходимо перенести в точку с координатами X=1.4 Y=2.35. На рисунке 2.2 изобразим преобразованную схему городского района. 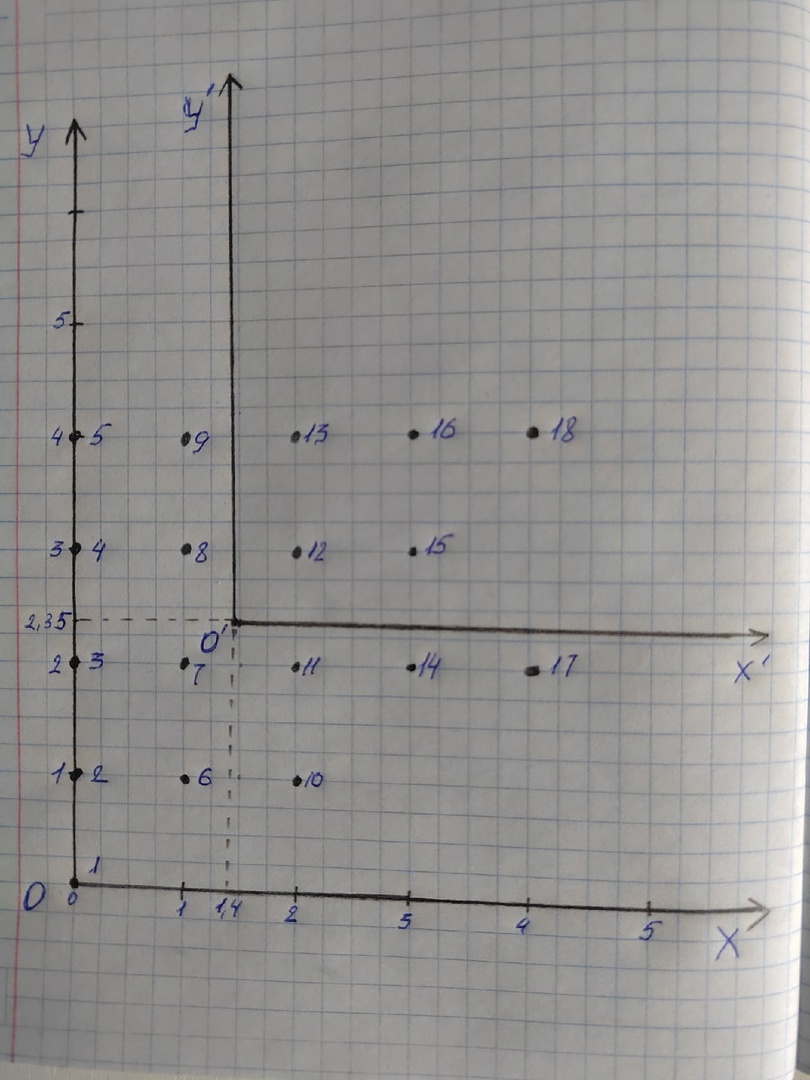 Рисунок 2.2 преобразованная схема городского района. С использованием рисунка 2.2 определим координаты расположения кварталов относительно нового местоположения кассы, обозначенного О’. При помощи теоремы Пифагора найдем расстояния di – расстояние первоначального месторасположения кассы до i- го квартала и di0 – это расстояния от оптимизированного месторасположения кассы до i – го квартала. di= 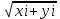 , di0= , di0=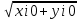 . .При помощи формулы Tiф= 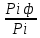 Найдем Tiф - фактическую долю потенциальных пассажиров i – го квартала, пользующимися услугами кассы в ее исходном положении. Для определения вида функции тяготения спроса необходимо найти коэффициенты a и b , коэффициент с нам известен он равен 1. Для того чтобы найти a и b нам необходимо определить расстояние D, при котором жители данного квартала перестают пользоваться услугами кассы. То есть такое D, при котором Pi будит ровняться 0. Из схемы видно что жители 19 – го квартала уже не пользуются услугами данной авиакассы, то есть на расстоянии d18=5,66 км от исходного положения кассы P=0, значит параметр D принимаем равным 5,66 км. Затем определим параметр β – это доля жителей, пользующихся данной кассой и удаленных на расстояние d= 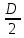 , от сюда d= , от сюда d=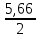 =2,83 км. Этому расстоянию соответствуют квартал 11, для которого T11ф=0,45 данная величина принимается в качестве β. По ранее выведенным формулам находим a и b. =2,83 км. Этому расстоянию соответствуют квартал 11, для которого T11ф=0,45 данная величина принимается в качестве β. По ранее выведенным формулам находим a и b.a= 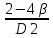 = =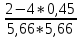 =0,006; =0,006;b= 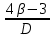 = =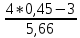 =-0,212. =-0,212.Таким образом функция тяготения спроса для кассы в ее изначальном положении имеет вид: T=0,006*d2-0,212*d+1. Считая что перенос кассы не влияет на вид функции тяготения спроса, это позволит определить Pi0 число пассажиров которые будут пользоваться кассой в ее новом положении. Pi0=Ti0*Pi , i=1,…,18. Где Ti0 доля потенциальных клиентов которые будут пользоваться услугами кассы в ее новом положении. Ti0=0,006*di02-0,212*di0+1, i=1,…,18. Где di0 – расстояние от i – го квартала до кассы в ее новом положении. Определим его по формуле: di0= 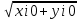 Результаты расчетов приведем в таблице 2.1. Таблица 2.1 оптимизация расположения кассы. 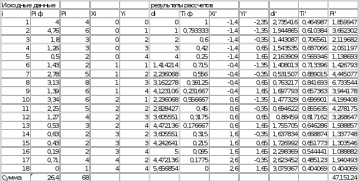 Как следует из данных таблицы 2.1, общее число пассажиров которые будут пользоваться услугами кассы в ее новом положении 47,151 тыс. чел. , а число пассажиров, пользующихся услугами кассы в ее исходном положении 26,4 тыс. чел. Таким образом при переносе кассы на новое месторасположения, позволит увеличить число клиентов на 47,151-26,4=20,751 тыс. чел., или 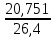 *100%=78,6% от первоначального числа, что говорит о целесообразности переноса кассы на новое местоположение. *100%=78,6% от первоначального числа, что говорит о целесообразности переноса кассы на новое местоположение.ЗАКЛЮЧЕНИЕ В курсовом проекте мы рассмотрели меняющуюся со временем единицу и сделали прогноз на то, как она изменится на следующие три года. Безусловно, нельзя его принимать за истину, так как изменение данной единицы зависит от множества параметров, которые мы не рассматривали, но мы можем проследить динамику ее развития. Так же мы рассмотрели расположение кассы по продаже авиабилетов и проанализировали эффективность ее работы на основании результатов ее работы. Выявили, что она не полностью использует свой потенциал, и нашли наиболее выгодное месторасположение, находясь в котором, она приносила бы максимальную прибыль за счет обслуживания наибольшего количества клиентов. Знания, полученные в процессе решения курсового проекта могут пригодится для успешного ведения своего бизнеса, при установлении его рентабильности. СПИСОК ЛИТЕРАТУРЫ Андронов А.М. , Хижняк А.Н. математические методы планирования и управления производственно – хозяйственной деятельностью предприятий гражданской авиации. – М.: «Транспорт» , 1977. – 215с. Яшкин А.Р. , Болотов Б.Н. Теоретические основы организации перевозок и коммерческой эксплуатации воздушного транспорта. Учебное пособие. – Л.: ОЛАГА, 1982 – 104С. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
