Теплофизические свойства материала. Задание на курсовую работу теплофизические свойства материала
 Скачать 0.68 Mb.
|
|
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ Теплофизические свойства материала
Параметры режима сварки
Рассчитать температурное поле ЭВМ. По полученным данным на масштабно-координатной бумаге формата А4 построить графики зависимости температурного поля: Т1(x, y, z)=f1(x) для y·10-3: 0, 10, 20, 30, 50 мм; Т2(x, y, z)=f2(±y) для x·10-3: 0, -10, -20, -50, -100 мм. Определить температуру в начале, середине и конце сварного шва, длина которого 200 мм, через 12 с после окончания сварки. Определить изотермы Т=1560 К, Т=1200 К, Т=800, Т=500 К на поверхности тела. Результаты расчета изотерм привести в виде табличных данных и графиков 4-х изотерм на масштабно-координатной бумаге формата А4. Сделать вывод КРАТКИЕ ТЕОРИТИЧЕСКИЕ СВЕДЕНИЯ Температурное поле есть распределение температур в теле в конкретный момент времени. Температура в общем случае может являться не только функцией координат х, у,z отдельных точек, но и функцией времени T=T(x,y,z,t).В последнем случае температурное поле является объемным. Оно может быть также плоским T=T(x,y,t) или линейный T=T(x,t). В расчетах тепловых процессов при сварке широко используют зависимости, полученные путем схематизации и упрощения действительных процессов распространения теплоты. . Источники теплоты принимают либо сосредоточенными, либо распределенными по соответствующему закону, который позволяет относительно просто описать процесс распространения теплоты. . Формы тела упрощают. . Теплофизические коэффициенты l, а, сr, a принимают не зависящими от температуры. Это допущение хотя и искажает действительный процесс распространения теплоты в теле, но значительно упрощает математические выражения. Указанные допущения позволяют получить стройную теорию распределения температуры в телах при нагреве их различными движущимися источниками теплоты. Эта теория хорошо отражает качественную картину, а в ряде случаев дает также и достаточную для технических расчетов точность описания сварочных процессов. Наибольшие погрешности в описании полей температур наблюдаются в зонах вблизи действия источников теплоты. В отдельных точках, где находятся сосредоточенные источники, расчетная температура достигает бесконечно больших значений. Определение температур в этих зонах в целях установления их значений по изложенным здесь методикам производить не следует. Математический аппарат теории, дополненный экспериментальными данными, а также описанием существа физических явлений, является удобным инструментом для выражения процессов распространения теплоты при сварке. В случае применения подвижного сосредоточенного источника тепла (электрическая дуга, электронный луч) изменение температурного поля в свариваемом изделии в начальный момент времени определяет меньшие области повышенных температур. По мере увеличения времени действия источника размеры этих областей возрастают до определенных значений и остаются неизменными при нормальных параметрах режима до завершения сварки. После прекращения действия подвижного источника охлаждение металла происходит интенсивнее, так как ввод тепла прекращен, а введенное тепло только распространяется в теле и отдается в окружающую среду конвективным путем или посредством радиации. В связи с этим различают три стадии изменения температурного поля: теплонасыщение, когда его размеры в подвижной системе координат, связанной с источником, увеличиваются; предельное, или установившееся состояние, когда температурное поле, оставаясь одинаковым, перемещается вместе с источником тепла (квазистационарное температурное поле); выравнивание температуры, когда источник тепла перестает действовать. Случай 1. Сварка выполняется за один проход с полным проплавлением изделия, что обеспечивает равномерное тепловыделение и установление одинаковых температур по толщине элемента. Такое распределение теплоты в изделии наблюдается при выполнении стыковых и угловых швов на тонколистовых конструкциях, а также при однопроходной сварке встык листов средней и большой толщины интенсивными источниками. В этом случае сварочную дугу (электронный луч, газовое пламя) можно представить как подвижный линейный источник теплоты, действующий в пластине, температурное поле которого определяется выражением:  . (1)Предельное значение температуры, характерное для сварки большей части длины достаточно протяженных швов, определяется по формуле:  . (2)Случай 2. Сварка или наплавка выполняется на массивном элементе (значительная толщина изделия). Тепловой поток преимущественно за счет теплопроводности отводится в толщину металла. В этом случае сварочный источник представляется как подвижный точечный, действующий на поверхности полубесконечного тела. Температурное поле определяется уравнением  , (3) . (4)Случай 3. Если сварка элементов средней толщины выполняется за один или несколько проходов и при этом по толщине листа температура в точках с одинаковыми координатами "х" и "у" существенно отличается, то сварочный источник представляется как точечный, действующий на поверхности плоского слоя. Принимают, что обе поверхности пластины не пропускают теплоту. Для учета отражения теплоты источника О от границы I вводят фиктивный точечный источник О1 (рис. 1). В свою очередь теплота от фиктивного источника О1 будет отражаться от поверхности II. Для учета этого вводят фиктивный источник теплоты О2 на расстоянии 2d от плоскости II. Теплота источника О2 будет отражаться от границы I, что требует введения фиктивного источника О3. Этот процесс может быть продолжен до бесконечности. Суммирование температурных полей от всех точечных источников мощностью q, перемещающихся со скоростью u в предельном состоянии дает уравнение:  ; (5)=x2+ y2+(z - 2nd)2; r2=x2+ y2.где Rn2 - расстояния элемента пластины А(x, y, z) от n - ого источника с координатами (0,0,2nd) (рис. 1). 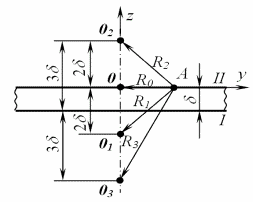 Упрощая (5) для случая квазистационарного (t®¥)температурного поля получаем расчетное выражение:  (6)Т.к. расчеты по формуле (6) довольно сложны, то температурное поле вне оси Оz на верхней (z = 0) и нижней (z = δ) плоскостях можно описать формулой:  , (5)где при отсутствии теплоотдачи с поверхностей:  . (6)(r, z) - коэффициент, выражающий отношение приращения температуры на поверхности плоского слоя, нагреваемого точечным источником, к приращению температуры пластины, вызываемому линейным источником, определяется по номограмме. Для z=0 m>1, для z=δ m <1. В приведенных выше выражениях приняты следующие обозначения:- эффективная мощность источника теплоты, Вт; u - скорость перемещения источника, м/с; λ - коэффициент теплопроводности металла, Вт/(м·К); δ - толщина свариваемых листов, м; с - удельная теплоемкость металла, Дж/(кг·К); ρ - плотность материала, кг/ м3; а - коэффициент температуропроводности металла, м2/с;, y, z - координаты рассматриваемой точки в подвижной системе координат, начало которой жестко связано с источником теплоты, м;  - плоский радиус-вектор (расстояние от рассматриваемой точки до источника теплоты), м; - пространственный радиус-вектор (расстояние от рассматриваемой точки до источника теплоты), м; - коэффициент температуроотдачи, с-1;α - коэффициент теплоотдачи, Вт/(м2·К); ψ2(ρ2, τ2) - коэффициент теплонасыщения для линейного источника в неограниченной пластине. Значение ψ2 на стадии теплонасыщения определяют по номограмме в зависимости от безразмерных критериев расстояния ρ2 и времени τ2:  ; (7) . (8)ψ3(ρ3, τ3) - коэффициент теплонасыщения для точечного источника в полубесконечном теле. Значение ψ3 определяют по номограмме в зависимости от безразмерных критериев расстояния ρ3 и времени τ3:  ; (9) . (10)К0 - функция Бесселя 1-го рода нулевого порядка. ВЫЧИСЛЕНИЕ ТЕМПЕРАТУРНОГО ПОЛЯ сварка температура теплота Для расчета температурного поля на стадии предельного состояния используется программа, составленная на языке Бейсик. Оценка тепловой обстановки в области действия сварочного источника выполняется на поверхности тела размерами 210´100 мм. Таблица 1. Результаты вычислений температуры предельного состояния
По полученным данным на масштабно-координатной бумаге формата А4 строятся графики температурного поля: Т1(x, y, z)=f1(x) для y·10-3: 0, 10, 20, 30, 50 мм; Т2(x, y, z)=f2(±y) для x·10-3: 0, -10, -20, -50, -100 мм. ПЕРИОД ВЫРАВНИВАНИЯ ТЕМПЕРАТУРЫ После окончания действия источника, введенное тепло продолжает распространяться в теле вследствие теплопроводности. Период процесса распространения тепла, начиная от момента прекращения действия источника, называется периодом выравнивания температуры. Для оценки температурного поля в этот период времени используем расчетную схему, предложенную Н.Н. Рыкалиным. 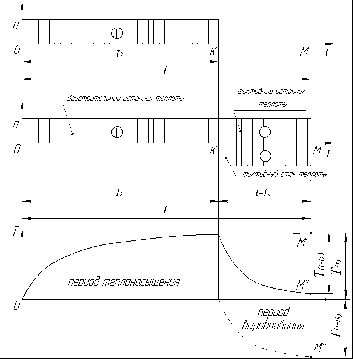 Рис. 2. Схема действия фиктивных источника и стока тепла в теле в период выравнивания температур Предположим, что после прохождения отрезка ОК источник мощностью q, прекративший ввод тепла в тело в момент нахождения его в точке К (рис. 2, а), продолжает действовать и дальше (вплоть до отдаленной точки М) как фиктивный источник той же мощности (рис. 2, б). Одновременно в момент К введен и фиктивный сток тепла мощностью -q, приложенный к тем же участкам тела, что и фиктивный источник +q, т. е. на участке КМ тело тепла не получает. Температуру ТВ в момент М в периоде выравнивания можно представить как алгебраическую сумму температуры Т(t) от продолжающего действовать источника +q и температуры -Т(t-tк) от начавшего действовать стока тепла - q (рис. 2, в):  . (11)Обе температуры можно выразить через температуру предельного состояния ТПР и соответствующие коэффициенты теплонасыщения:  . (12)Значения коэффициентов  определяют по соответствующим номограммам (рис. 25). В расчетах периода выравнивания полагают, что фиктивный источник и сток движутся так же, как двигался бы действительный источник, перенося с собой и начало подвижной системы координат.ВЫЧИСЛЕНИЕ ТЕМПЕРАТУР Задание На поверхности полубесконечного тела из сплава ХН78Т ручной дуговой сваркой наплавляют валик длиной l=150 мм. Режим наплавки: U=28 B; I=220 A; u = 1×10-3 м/с. Рассчитать температуру в начале, середине и в конце сварного шва через 10 с (tH) после окончания сварки. В соответствии с заданным способом сварки принимаем тепловой КПД равным 70%. Мощность источника теплоты:  Дж/с.Теплофизические свойства металла:  Вт/(м·К);  м2/с.При наплавке действительный точечный источник на длине шва 160 мм перемещается со скоростью u = 1 мм/с. Длительность его действия:= l/u = 160/1 = 160 с. После окончания сварки фиктивный источник и сток, двигаясь с той же скоростью, через 10 с находятся в точке, удаленной от конца шва на расстояние хм хм = u× tH = 1×10 = 10 мм. Координаты начала, середины и конца шва относительно фиктивного источника и стока х0 = - l - хм = -160-10 = -170 мм; у0 = 0; z0 = 0. хN = - l/2 - хм = -160/2 - 20 = -100 мм; уN = 0; zN = 0. хк = - хм = -10 мм; ук = 0; zк = 0. Предельные температуры начала, середины и конца шва определим по рассчитанной ранее таблице. начала шва Т(-170;0;0) = 138 K середины шва Т(-100;0;0) = 235 K конца шва Т(-10;0;0) = 2353 K Длительность действия действительного и фиктивного источников = 160 + 10 = 170 c. Длительность действия фиктивного стока t - tk = 10 с. Безразмерные критерии для нахождения коэффициентов теплонасыщения: расстояния начала шва  ;середины шва  ;конца шва  .времени действия источников:  ;времени стока:  .Соответствующие коэффициенты теплонасыщения по номограмме: начала шва ψ3 = 0,63 и ψ3΄ = 0; середины шва ψ3 = 0,84 и ψ3΄ = 0; конца шва ψ3 = 1 и ψ3΄ = 0,95. Температуры через 10 с после окончания наплавки: начала шва Т0 = 138(0,63 - 0) = 87 K; середины шва ТN = 235(0,84 - 0) = 198 K; конца шва ТK = 2353(1-0.95) = 118 K. БЫСТРОДВИЖУЩИЕСЯ ИСТОЧНИКИ ТЕПЛОТЫ В сварочной технике все чаще применяются мощные источники теплоты, осуществляющие сварку с весьма большими скоростями. В предельном случае, когда q и v стремятся к бесконечности, в то время как отношение q/u сохраняет некоторое конечное значение (q®¥; u®¥; q/u=const), распространение теплоты приобретает особенности, позволяющие значительно упростить расчетные схемы. Определение температурного поля выполняют по уравнениям: для точечного источника  ; (13)для линейного источника  . (14)где t - время, отсчитываемое от момента, когда источник тепла пересек плоскость y00z0, в которой находится рассматриваемая точка; y0, z0 - неподвижные координаты рассматриваемой точки. Применительно к рассматриваемым схемам можно аналитическим способом выразить связь между координатами точек изотермы определенной температуры. Заменив в формулах (14) и (15) ut на [-x] и направление оси х на обратное, можно получить соответственно следующие уравнения поверхностных изотерм температурного поля быстродвижущихся точечного и линейного источников (без учета отдачи тепла поверхностью):  ; (15) .Таблица 2. Изотермы поверхности тела
ВЫВОД В данной курсовой работе температурное поле можно вычислить как по формулам так и с помощью ЭВМ. Весьма эффективно использование ЭВМ в задачах оптимизации параметров режимов сварки, например по скорости охлаждения в заданном интервале температур. Выразить в явном виде скорость охлаждения при определенном значении Т не удается. Подбор оптимальных q и u для обеспечения заданной скорости охлаждения в конкретном интервале температур, в особенности, если еще ставится задача минимизации длительности пребывания металла выше определенной температуры, без ЭВМ практически невозможен. Особый случай расчета тепловых процессов, который может быть выполнен и использованием только крупных ЭВМ- расчет с учетом зависимости теплофизических характеристик металла от температуры. В данной курсовой работе можно рассчитать температуру любой точки сварного шва, но следует заметить, что в ряде случаев реальные процессы и явления протекают сложнее, чем это описывается формулами. Часто характер теплового воздействия при сварке, условия распространения теплоты и теплоотдачи от свариваемых деталей настолько сложны или неопределимы, что расчетное распределение температур становится либо затруднительным, либо настолько неточным, что его использование оказывается неоправданным. Экспериментальное определение температур при сварке имеет свои преимущества перед расчетным, хотя и уступает ему в возможности получения анализа общих закономерностей. Правильным следует считать подход, при котором оба метода дополняют друг друга. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 1. Теория сварочных процессов/ Под ред. В.В. Фролова. М.: Высшая школа, 1988. 559 с. 2. Теория сварочных процессов/ Г.Д. Петров, А.С. Тумарев. М.: высшая школа, 1977. 392 с. . Сварка в машиностроении/ Под ред. А.И. Акулова. М.: Машиностроение. 1978. 462 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||