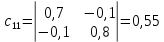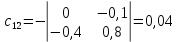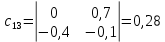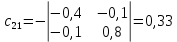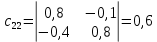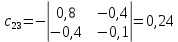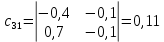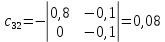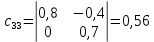геометрия. МОБ_В7_Заказ_4791805_14_05_22. Задание Найти оптимальный сбалансированный выпуск продукции по модели межотраслевого баланса ХАХУ. Исходные данные формируются по номеру варианта (выбор параметра m)
 Скачать 43.45 Kb.
|
|
Задание 3. Найти оптимальный сбалансированный выпуск продукции по модели межотраслевого баланса Х=АХ+У. Исходные данные формируются по номеру варианта Таблица 1 (выбор параметра - m)
Таблица 2 (выбор параметра - n )
Три отрасли промышленности I, II и III являются производителями и в то же время потребителями некоторой продукции. Их взаимосвязи определяет матрица A коэффициентов прямых затрат 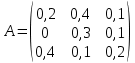 в которой число  aij, стоящее на пересечении i -ой строки и j -го столбца равно 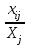 , где xij - поток средств производства из i -ой отрасли в j -ую, а Xj - валовой объем продукции j -ой отрасли (все объемы продукции выражаются в единицах стоимости). Задан также вектор объемов конечной продукции.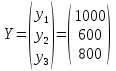 1. Составить уравнение межотраслевого баланса. 2. Решить систему уравнений межотраслевого баланса, то есть найти объемы валовой продукции каждой отрасли X1,X2 ,X3, обеспечивающие потребности всех отраслей и изготовление конечной продукции Y. (Расчеты производить с точность до двух знаков после запятой). 3. Составить матрицу Х потоков средств производства xij. 4. Определить общие доходы каждой отрасли 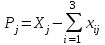 .5. Результаты расчетов оформить в виде таблицы межотраслевого баланса:
Решение. 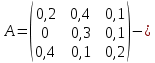 матрица коэффициентов прямых материальных затрат;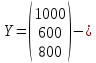 вектор конечного продукта.Коэффициенты прямых материальных затрат показывают объем материальных ресурсов i-го вида, необходимый для производства единицы валового продукта j-го вида. Матрица А продуктивна, т.к. для всех столбцов сумма элементов меньше единицы. Уравнение межотраслевого баланса в матричной форме: 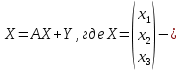 вектор валового выпуска.Для того, чтобы найти объемы валовой продукции каждой отрасли, перепишем уравнение межотраслевого баланса в следующем виде: 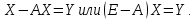 Откуда 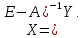 Находим матрицу С = Е – А и обратную к ней матрицу полных затрат В = (Е – А)-1. 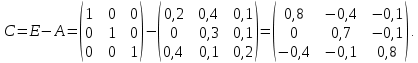 Определитель этой матрицы: 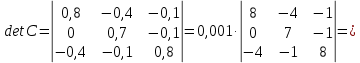 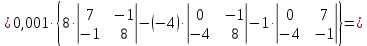 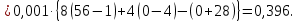 Алгебраические дополнения элементов матрицы C = Е – А:
Обратная матрица, представляющая собой таблицу коэффициентов полных затрат, будет следующей: 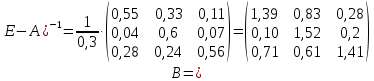 Находим объемы валовой продукции каждой отрасли: 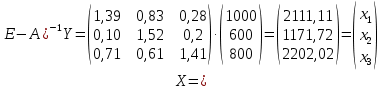 Межотраслевые поставки найдем по формуле xij = aij·xj (i, j = 1, 2, 3) Межотраслевой баланс состоит из четырех квадрантов (табл.). Первый квадрант отражает межотраслевые потоки продукции. Второй характеризует отраслевую материальную структуру национального дохода. Третий представляет национальный доход как стоимость условно-чистой продукции (Zj), равной сумме амортизации (cj), оплаты труда (vj) и чистого дохода j-й отрасли (mj). Четвертый квадрант показывает конечное распределение и использование национального дохода. Составляющие третьего квадранта (условно-чистая продукция) находятся как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта: Zj = Xj - ∑xij Величина условно чистой продукции Zi равна сумме амортизации, оплаты труда и чистого дохода отрасли j. 2111,11 - (422,22 + 0 + 844,44) = 844,44 1171,72 - (468,69 + 351,52 + 117,17) = 234,34 2202,02 - (220,2 + 220,2 + 440,4) = 1321,22 Межотраслевые поставки продукции: 0,2·2111,11 = 422,22; 0,4·1171,72 = 468,68; 0,1·2202,02 = 220,2; 0·2111,111 = 0; 0,3·1171,72 = 351,54; 0,1·2202,02 = 220,2; 0,4·2111,11 = 844,44; 0,1·1171,72 = 117,17; 0,2·2202,02 = 440,4;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
