Алгоритм Форда - Фалкерсона. решение_граф. Задание Построить граф и найти его максимальную пропускную способность (Алгоритм Форда Фалкерсона)

Название	Задание Построить граф и найти его максимальную пропускную способность (Алгоритм Форда Фалкерсона)
Анкор	Алгоритм Форда - Фалкерсона
Дата	28.04.2022
Размер	1.79 Mb.
Формат файла
Имя файла	решение_граф.docx
Тип	Документы #501824

Вариант – 13

На ориентированном графе с вершинами: 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10 и ребрами соединяющими: А-(1 и 2); B-(1 и 5); C-(1 и 7); D-(2 и 3); E-(2 и 10); F-(3 и 4); G-(3 и 6); H-(3 и 10); I-(4 и 5); J-(4 и 6); K-(5 и 6); L-(5 и 7); M-(5 и 8); N-(6 и 7); O-(6 и 8); Q-(7 и 8); P-(8 и 9); R-(9 и 10);

Каждому ребру присваивается значение параметра, называемого «пропускной способностью». Оно характеризует объем пропускаемого по ребру продукта за единицу времени в направлении возрастания номеров вершин, соединяемых им. Эти значения следующие: А(6); B(2); C(1); D(8); E(2); F(9); G(7); H(5); I(5); J(4); K(2); L(6); M(3); N(7); O(7); Q(5); P(9); R(4);

Задание: Построить граф и найти его максимальную пропускную способность (Алгоритм Форда - Фалкерсона)

Переменными математической модели данной индивидуальной задачи о максимальном потоке в сети являются 10 переменных: x12, x13, x23, x24, x25, x34, x35, x45, x46, x56. Каждая из этих переменных xij может принимать неотрицательные целочисленное значение, не превышающее пропускной способности дуги cij и соответствующее величине потока продукта, транспортируемого по отдельному ребру, связывающему вершины сети. Тогда математическая постановка рассматриваемой индивидуальной задачи о максимальном потоке в сети может быть записана в следующем виде:

где множество допустимых альтернатив

формируется следующей системой ограничений типа равенств и неравенств:

Заметим, что те переменные xij, для которых весовая функция дуг h не определена или равна 0, не входят в математическую постановку рассматриваемой задачи.

Для решения поставленной задачи воспользуемся программой электронных таблиц MS Excel – компонентом офисного пакета MS System Office. MS Excel позволяет выполнять быстрые расчеты и содержит встроенные средства для решения задач оптимизации. Также имеющиеся возможности MS Excel могут быть расширены за счет использования встроенного языка программирования VBA или вызова внешних функций из библиотек динамической компоновки, разработанных самим пользователем на таких языках программирования как Borland Delphi® и MS Visual C++®.

Для решения поставленной индивидуальной задачи нахождения максимального потока в сети с помощью программы MS Excel необходимо выполнить следующие действия.

№	x	y
1	15	5
2	8	7
3	20	6
4	27	8
5	11	9,5
6	25	11
7	5	12
8	17	13
9	30	14
10	15	15

1. Создать в книге новый рабочий лист с именем «Максимальный поток».

2. Ввести необходимые надписи в ячейки A1:F1 (рис. 1). Конкретное содержание этих надписей не оказывает влияния на решение рассматриваемой задачи.

3. В ячейки A2:A11 ввести индексы начальных вершин, а в ячейки B2:B11 – индексы конечных вершин всех имеющихся дуг исходного графа.

4. В ячейки C2:C11 ввести значения пропускных способностей дуг исходного графа.

5. В ячейку F2 ввести формулу: =СУММ(D2:D3), которая представляет целевую функцию (15.5).

6. В ячейку E2 ввести формулу: =СУММ(D2:D3)-СУММ(D10:D11), которая представляет собой левую часть первого ограничения (15.6).

7. В ячейку E3 ввести значение левой части второго ограничения: D2-СУММ(D4: D6).

8. В ячейку E4 ввести значение левой части третьего ограничения: СУММ(D3:D4)-СУММ(D7: D8).

9. В ячейку E5 ввести значение левой части четвертого ограничения: СУММ(D5; D7)-СУММ(D9: D10).

10. В ячейку E6 ввести значение левой части пятого ограничения: СУММ(D6; D8:D9)-D11.

Внешний вид рабочего листа с исходными данными для решения задачи о минимальном пути в графе имеет следующий вид (рис 1).

Рис. 1. Исходные данные для решения задачи о максимальном потоке в сети

Для дальнейшего решения задачи следует вызвать мастер поиска решений для чего необходимо выполнить операцию главного меню: Сервис | Поиск решения.

После появления диалогового окна Поиск решения следует выполнить следующие действия:

1. В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $F$2.

2. Для группы Равной: выбрать вариант поиска решения – максимальному значению.

3. В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $D$2:$D$11.

4. Задать 3 ограничения для рассматриваемой задачи. С этой целью выполнить следующие действия:

· для задания этих ограничений в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;

· в появившемся дополнительном окне выбрать диапазон ячеек $E$2:$E$6, который должен отобразиться в поле с именем Ссылка на ячейку;

· в качестве знака ограничения из выпадающего списка выбрать равенство «=»;

· в качестве значения правой части ограничения ввести с клавиатуры значение 0;

· для добавления следующего ограничения в дополнительном окне нажать кнопку с надписью Добавить.

5. Задать следующее ограничение на пропускные способности дуг (15.6). С этой целью выполнить следующие действия:

· Для задания ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;

· В появившемся дополнительном окне выбрать блок $D$2: $D$11, который должна отобразиться в поле с именем Ссылка на ячейку;

· В качестве знака ограничения из выпадающего спуска выбрать нестрогое неравенство «<=».

· В качестве значения правой части ограничения в появившемся дополнительном окне выбрать блок ячеек $C$2: $C$11, который должна отобразиться в поле с именем Ссылка на ячейку;

· Для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить.

6. Задать ограничение на целочисленные значения переменных. С этой целью выполнить следующие действия:

· В исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;

· В появившемся дополнительном окне выбрать диапазон ячеек $D$2:$D$11, который должен отобразиться в поле с именем Ссылка на ячейку;

· В качестве знака ограничения из выпадающего списка выбрать строку «цел»;

· В качестве значения правой части ограничения в поле с именем Ограничение: оставить без изменения вставленное программой значение «целочисленные»;

· Для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить.

8. В окне дополнительных параметров поиска решения выбрать отметки Линейная модель и Неотрицательные значения.

Общий вид диалогового окна спецификации параметров мастера поиска решения показан на рис. 2.

Рис. 2. Ограничения значений переменных и параметры мастера поиска решения для задачи о максимальном потоке в сети

Рис. 3. Результат количественного решения задачи о максимальном

потоке в сети

После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет следующий вид (рис. 3).

Результатом решения задачи о максимальном потоке в сети являются найденные оптимальные значения переменных: x₁₂=3, x₁₃=2, x₂₄=1, x₂₅=2, x₃₄=2, x₃₅=1, x₄₆=2, x₅₆=3 , остальные переменные равны 0. найденному оптимальному решению соответствует значение целевой функции: f_cpt=3

Анализ найденного решения показывает, что максимальный поток в сети (рис. 15.2), проходящий из вершины 1 в вершину 6, протекает по следующим дугам: по дуге (1, 2) в количестве 3 т/час, по дуге (1, 3) в количестве 2 т/час, по дуге (2, 4) в количестве 1 т/час, по дуге (2, 5) в количестве 2 т/час, по дуге (3, 4) в количестве 2 т/час, по дуге (3, 5) в количестве 21т/час, по дуге (4, 6) в количестве 2 т/час, по дуге (5, 6) в количестве 3 т/час.

Тем самым найден оптимальный план транспортировки продукта от пункта старта до пункта завершения. При этом общая величина потока транспортируемого продукта для рассматриваемой сети будет максимальна и равна 3 т/час.

Рисунок 4 Координаты вершин графа

Эта таблица располагается в блоке ячеек А1:С11 на листе 2. В ней задаются координаты вершин графа, которые соответствуют этапам выполнения проекта. Их значения выбираются произвольно и в процессе работы с программой они могут корректироваться для получения лучшей наглядности графа.

Рисунок 5 Данные для построения ребер графа
Таблица (5) размещается в блоке ячеек Е1:М19 на листе 2 и используются для построения ребер графа. Столбцы «Н» и «К» заполняются путем копирования начальных данных, а столбцы x_н,y_н,x_к и y_кформируются с помощью функции ВПР() на множестве значений из блока H1:K19.

Столбцы x_ср и y_срформируются как средние значения столбцов x_н и x_к для x_{ср и}столбцов y_н и y_к для y_ср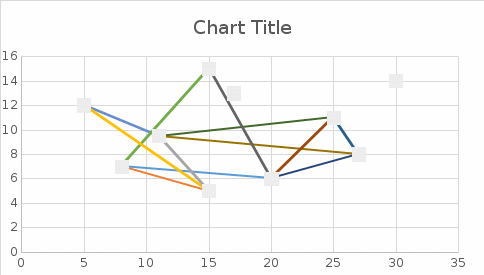

Рисунок 6 Граф процесса

Построение графа ( Рисунок ) производится графическими средствами Excel. Вначале по данным блока ячеек строится точечная диаграмма вершин графа (Рисунок )

Рисунок 7 Окно вставки точечной диаграммы

Для построения ребер графа необходимо щелчком правой кнопки мыши на области построения открыть окно ( Рисунок )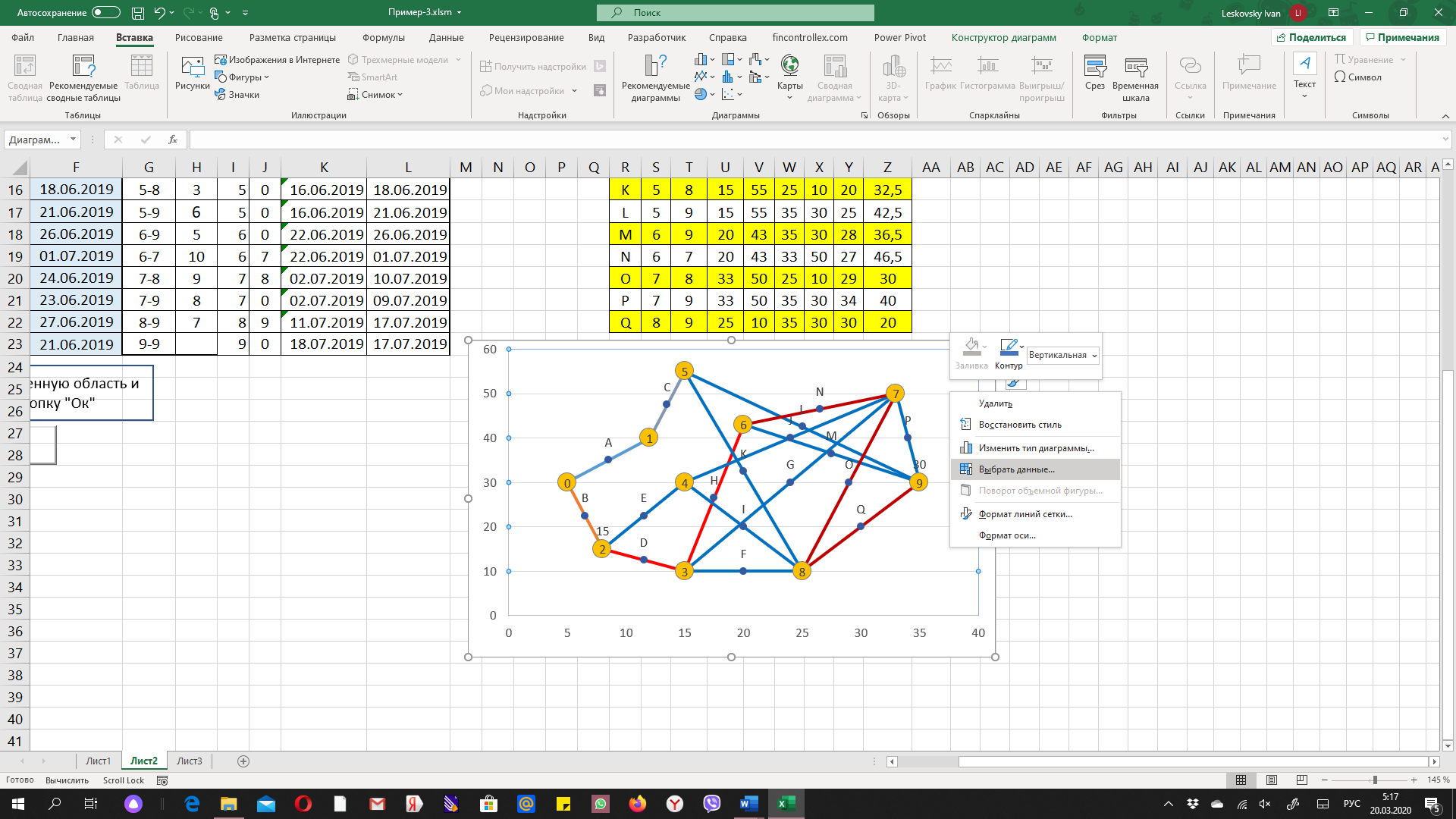

Рисунок 8 Активация окна Выбрать данные

В окне Выбрать данные активируется режим Добавить ( Рисунок )

Рисунок 9. Окно Выбрать данные

Рисунок 10 Окно добавить

В это окно вводятся данные из блока ячеек:

В поле «Имя ряда» щелчком мыши вводится одно из значений блока ячеек R6:R22;
В поле «Значение X» через «;» щелчком мыши вводятся соответствующие значения x_н и x_к
Поле «Значение Y» очищается, затем через «;» щелчком мыши в него вводятся соответствующие значения y_н и y_к.

Для дальнейших настроек элементов графа необходимо щелчком правой кнопки мыши активировать контекстное меню (Рисунок )

Рисунок 11 Меню для вызова окон преобразования элементов графа

С помощью инструментов вызываемых из этого меню редактируются форма , размеры и цвет узлов графа, содержание, расположение и шрифт надписей, толщина и цвет ребер.