Расчет трубопровода. Задача. Задание Расчет трубопровода. Вязкая сжимаемая жидкость (газ)
 Скачать 144.61 Kb. Скачать 144.61 Kb.
|
Задание 5. Расчет трубопровода. Вязкая сжимаемая жидкость (газ)Газ (воздух) через цилиндрическую трубу истекает в пространство с давлением РН=140 кПа. Движение газа в трубе – адиабатическое с трением. Заданы: длина L=2 м и диаметр трубы d=15 мм; материал из которого изготовлена труба; температура торможения газа Т0=300 К. Определить: давление торможения Р0вх необходимое для подачи заданного массового расхода газа G (G=70% от Gкрит) и зависимости параметров газового потока (скорости V, температуры Т, давления Р, плотности ρ) от координаты вдоль трубы. Величину эквивалентной шероховатости трубы принять равной 0,04 мм. Зависимости параметров газового потока как функции координаты вдоль трубы представить графически с указанием масштаба. Все массовые однотипные расчеты свести в таблицу. Указания: используются стандартные газодинамические функции 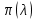 , , 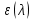 , , 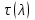 , , 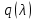 , , 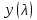 , зависящие от коэффициента скорости , зависящие от коэффициента скорости 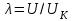 . U – скорость газа, Uк – критическая скорость газа - . U – скорость газа, Uк – критическая скорость газа - 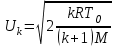 , где T0 – температура торможения, R=8,314 Дж/моль/К –универсальная газовая постоянная, M – молярная масса газа, кг/моль, , где T0 – температура торможения, R=8,314 Дж/моль/К –универсальная газовая постоянная, M – молярная масса газа, кг/моль, 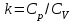 – показатель адиабаты газа. – показатель адиабаты газа.Решение: При составлении уравнений движения сжимаемой жидкости (газа) следует учитывать, что не только скорости, но и плотности, температуры и давления отдельных струек в пределах живых сечений неодинаковы, что значительно усложняет исследование. Поэтому поток конечных размеров рассматривают как одну струйку. Заменив в уравнении для струйки скорость струйки 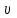 на среднюю скорость потока на среднюю скорость потока 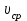 , можно сразу написать уравнение Бернулли сжимаемой невязкой жидкости: , можно сразу написать уравнение Бернулли сжимаемой невязкой жидкости: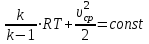 (5.1) (5.1)
Теперь составим уравнение Бернулли для вязкой сжимаемой жидкости, для чего запишем дифференциальное уравнение движения 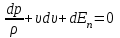 интегрирование которого для сжимаемой жидкости зависит от конкретных условий движения и закона изменения состояния газа. При адиабатическом течении, где отсутствует обмен тепла со средой вне границ потока, можно получить уравнение движения в конечном виде, для чего необходимо применить понятие энтальпии 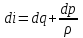 (5.2) (5.2)
где q – количество тепла, передаваемое 1 кг газа. Подставив уравнение энтальпии в уравнение Бернулли, получим 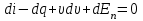 При адиабатическом течении энергия, потерянная на трение, переходит во внутреннее тепло (dEn = dq), тогда 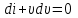 Проинтегрировав, получим 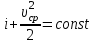 (5.3) (5.3)
Мы получили основное уравнение адиабатического течения газа. Вывод: Сумма удельной кинетической энергии и энтальпии остается неизменной в процессе движения газа. Из (5.3) следует, что в случае полного торможения потока газа энтальпия достигает максимального значения и обозначается как энтальпия торможения i0 , или полная энтальпия: 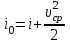 (5.4) (5.4)Поскольку 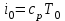 , то температура T0 называется температурой торможения. , то температура T0 называется температурой торможения.Теплоёмкость воздуха равна 1005 Дж/(кг·град), температура торможения газа Т0=300 К, откуда для воздуха в нашем примере, энтальпия торможения будет равна 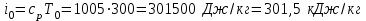 Для расчета применяют относительные скорости движения: - скорости звука, т.е. скорости распространения сигнала в упругой среде газов; - критической скорости – условной скорости потока. Скорость звука является однозначной зависимостью от местной статической температуры в потоке газа; критическая скорость однозначно зависит от температуры адиабатного торможения потока во входном сечении канала, если полагают, что эта величина в дальнейшем остается неизменной при изменении разности давлений на входе и выходе. При изменении перепада давлений в рассматриваемом канале происходит увеличение скорости движения потока. При неизменной площади сечения на выходе имеет место кризис течения – скорость движения потока при каком-то значении отношения давлений достигает скорости звука, и при дальнейшем увеличении перепада давлений не может возрасти. Этому моменту соответствует равенство единице как отношения скорости потока к скорости звука, так и отношения скорости потока к критической скорости. Отношение скорости потока к местной скорости звука называется числом Маха и записывается 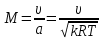 , (5.5) , (5.5) где Т –температура газа, К; 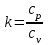 - показатель адиабаты, отношение теплоемкостей при постоянном давлении и объеме; R – газовая постоянная, Дж/(кг· град). - показатель адиабаты, отношение теплоемкостей при постоянном давлении и объеме; R – газовая постоянная, Дж/(кг· град).Для воздуха к=1,4, R=287 Дж/(кг·К). Число М может иметь любые значения от 0 и до бесконечности. Отношение скорости потока к критической скорости записывается: 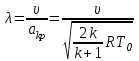 , (5.6) , (5.6) где Т0 - температура торможения, К. Для воздуха, в нашем примере критическая скорость равна 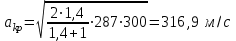 В энергетически изолированном течении максимальная скорость может быть получена тогда, когда полная энтальпия будет превращена в кинетическую энергию, то есть при расширении газа до абсолютного вакуума (i = 0, p = o). Тогда в соответствии с (5.4) имеем: 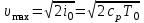 Для воздуха (cp = 1005 Дж/(кг∙град)) данная формула принимает следующий вид: 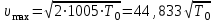 Для нашего примера: 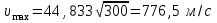 . .Число λ может достигать значения от 0 до 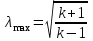 , для воздуха от 0 до 2,45. , для воздуха от 0 до 2,45. Естественно, удобнее зависимости параметров потока определять по значению λ, а число Маха связано с ним зависимостью: 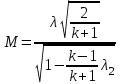 (5.7) (5.7)Для воздуха эта зависимость имеет вид: 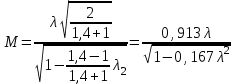 Скорость дозвукового потока может быть подсчитана по формуле: 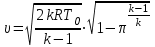 [1, с.10] [1, с.10]Газодинамические функции – это математические выражения, показывающие характеристики одномерного потока газов (связь между параметрами состояния), характеристики плотности потока, импульса силы и количества движения потока при изменении располагаемого перепада давлений на входе и выходе из рассматриваемого канала. Функции 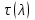 , , 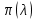 и и 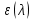 , характеризующие термодинамическое состояние газа. , характеризующие термодинамическое состояние газа.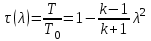 ; (5.8) ; (5.8)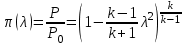 ; (5.9) ; (5.9)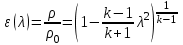 ; (5.10) ; (5.10)Функции 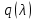 и и 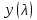 , характеризующие поток массы , характеризующие поток массы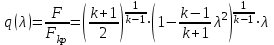 ; (5.11) ; (5.11)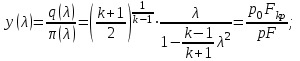 (5.12) (5.12)Расход газа G (кг/с), текущего по трубе, с помощью газодинамических функций q и y выражается в виде: 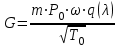 , , 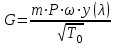 (5.13) (5.13)где P, P0 – давление и давление торможения газа, Па; - площадь поперечного сечения трубы, м2, параметр m определяется как 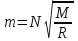 , , 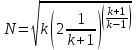 . (5.14) . (5.14)Критический расход газа Gк (расход при =1) определяется по формуле 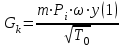 (5.15) (5.15)где Pн – противодавление, Па. При расчете распределений параметров газового потока по длине трубы принимаем расход равным 70% от критического. Закон сохранения массы при движении газового потока в трубе с постоянной площадью поперечного сечения позволяет для любых двух сечений 1 и 2 записать соотношения 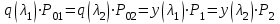 (5.16) (5.16)При адиабатическом течении газа с трением в трубе диаметром d коэффициент скорости изменяется от 1 в первом сечении до 2 во втором, находящемся на расстоянии l вниз по потоку в соответствии с уравнением 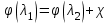 , где , где 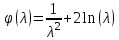 - специальная газодинамическая функция, - специальная газодинамическая функция, 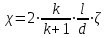 - приведенная длина трубы, - приведенная длина трубы, 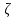 - коэффициент трения трубы (может быть вычислен по формуле Альтшуля - коэффициент трения трубы (может быть вычислен по формуле Альтшуля 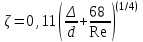 . Число Рейнольдса вычисляется по формуле . Число Рейнольдса вычисляется по формуле 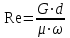 . .Из выражения для числа Рейнольдса следует, что оно изменяется при движении газа по трубе постоянного сечения только за счет зависимости динамической вязкости от температуры. Эта зависимость достаточно слабая и ей можно пренебречь. Поэтому значение 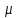 для вычисления числа Рейнольдса можно выбирать при температуре торможения используя формулу Сатерленда для вычисления числа Рейнольдса можно выбирать при температуре торможения используя формулу Сатерленда 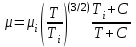 , , 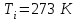 . .При адиабатическом движении газа в трубе постоянного сечения дозвуковой поток при наличии трения ускоряется. Поэтому максимальная скорость будет достигаться в выходном сечении трубы. Если G 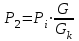 . Распределение скорости и температуры по длине трубы при G>Gк будет совпадать с распределением этих параметров при G=Gк. . Распределение скорости и температуры по длине трубы при G>Gк будет совпадать с распределением этих параметров при G=Gк. После определения всех параметров торможения могут быть определены температура и плотность движущегося газа: 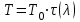 , , 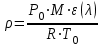 Для нашего примера расчета выберем следующие параметры: L=2,0 м, d=15 мм, PН=140 кПа, Т0=300 К, газ – воздух. Задаем термодинамические параметры газа: Молярная масса воздуха: M=0,02897 кг/моль, показатель адиабаты воздуха: k=1,4. Кинематическая вязкость воздуха – определяем при температуре торможения по формуле Сатерленда 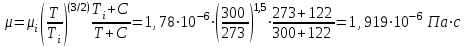 . Для воздуха . Для воздуха 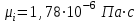 , С=122 K. , С=122 K. Вычисляем критическую скорость (по температуре торможения): 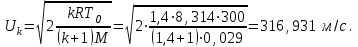 Вычисляем критический расход используя y(1.0): y(1)=1,8929, 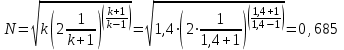 , , 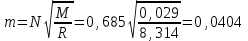 , , 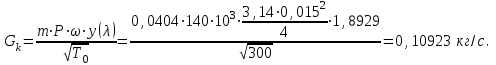 Определяем давление торможения P01 в зависимости от расхода G: Задаем расход G как долю критического расхода Gк. G=0.7Gк (G=0,07646 кг/с). Определяем число Рейнольдса, коэффициент трения и приведенную длину: 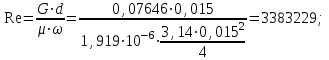 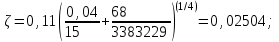 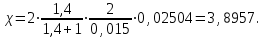 Так как G 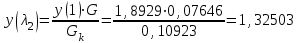 . .Из этого соотношения находим используя определение функции y: 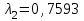 . . Тогда 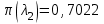 , , 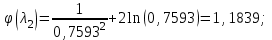 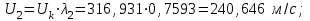 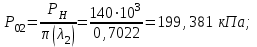 P2=140 кПа, P2=140 кПа,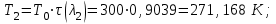 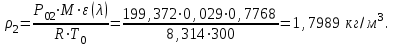 Используя соотношение между функциями 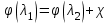 и уже известное значение и уже известное значение 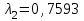 находим находим 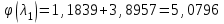 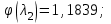 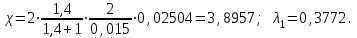 Тогда 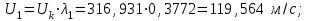 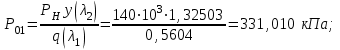 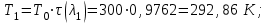 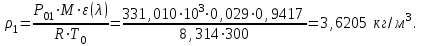 Определение распределения параметров движущегося газа вдоль трубы. Длину трубы разбиваем на равные отрезки точками с шагом 0,02L=0,02·2=0,04 м. Для каждого сечения определяем приведенные длины 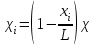 , а затем соответствующие им значения параметра решая на каждом шаге уравнение , а затем соответствующие им значения параметра решая на каждом шаге уравнение 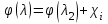 , где 2 – уже найденное значение параметра в выходном сечении. После нахождения параметра находим необходимые газодинамические функции и аналогично с входным сечением определяем Ui, P0i, Pi, Ti и i. Результаты расчета сводим в таблицу и представляем графически. , где 2 – уже найденное значение параметра в выходном сечении. После нахождения параметра находим необходимые газодинамические функции и аналогично с входным сечением определяем Ui, P0i, Pi, Ti и i. Результаты расчета сводим в таблицу и представляем графически.
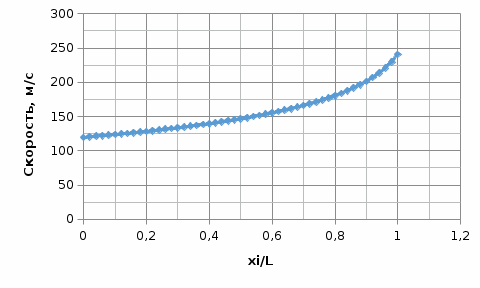 Рис.5.1. Зависимость скорости газового потока от координаты вдоль трубы 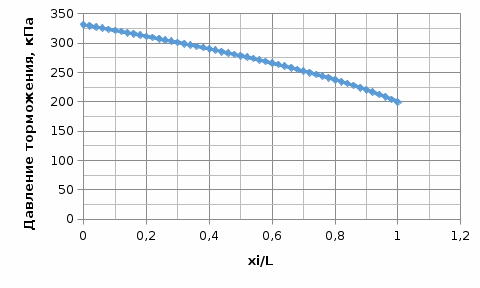 Рис.5.2. Зависимость давления торможения от координаты вдоль трубы 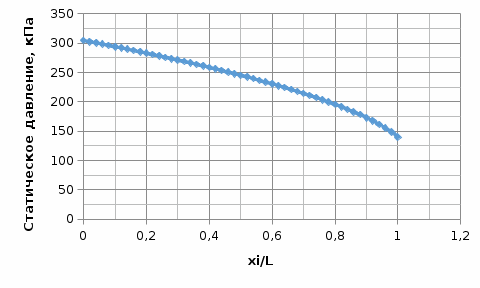 Рис.5.3. Зависимость статического давления от координаты вдоль трубы 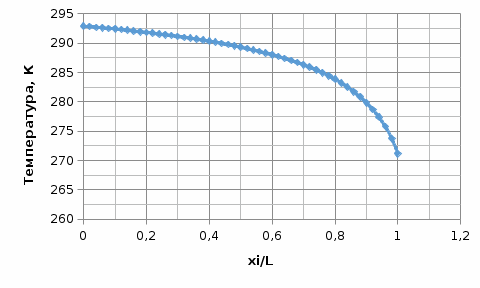 Рис.5.4. Зависимость температуры газового потока от координаты вдоль трубы 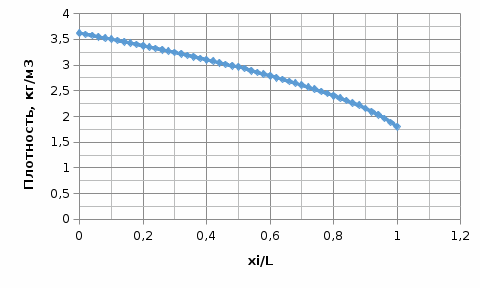 Рис.5.5. Зависимость плотности газового потока от координаты вдоль трубы |