Динамика задача 4 14 вариант. задача д4 14 вариант. Задание со стр. 73
 Скачать 107.83 Kb. Скачать 107.83 Kb.
|
Задание со стр. 73 Дано. Механизм расположен в горизонтальной плоскости. Водила О1О2: М, m3g=P, ѱ Шестарня 1: m1g=Q, R, φ Шестарня 2: m2g=Q, r 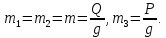 Трение отсутствует. Найти: 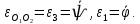 Решение. В рассматриваемом механизме водила O1О2 и шестеренка 1 вращаются независимо друг от друга вокруг общей оси О1. При движении механизма шестерни 1 и водила O1О2 вращаются вокруг оси O1, шестерня 2 совершает плоскопараллельное движение. Система имеет две степени свободы: мы можем закрепить шестеренку 1, отобрав у механизма одну степень свободы, но механизм при этом не теряет подвижности: водила O1О2 может вращаться вокруг оси O1, приводя в движение шестеренку 2. Если же закрепить и водила O1О2, то механизм потеряет подвижность. 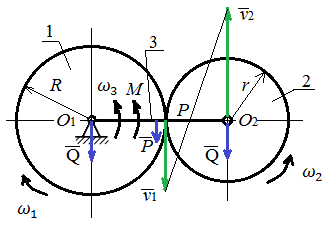 Скорости тел через обобщённые скорости: 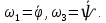 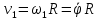 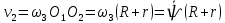 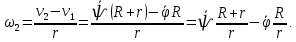 Кинетическая энергия системы равна: 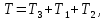 Кинетическая энергия водилы O1O2: 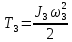 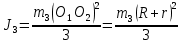 Кинетическая энергия шестерни 1: 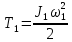 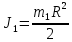 Кинетическая энергия шестерни 2: 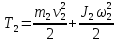 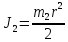 Выражение для кинетической энергии системы принимает вид: 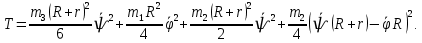 Подставив сюда заданные значения масс, получим: 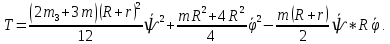 Потенциальная энергия системы Так как механизм расположен в горизонтальной плоскости, то высота центральной тяжести тел не меняется, поэтому 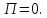 Обобщённые силы на возможных скоростях Для нахождения обобщенной силы Qѱ, фиксируем координату , даём координате ѱ приращение ѱ, при этом точка О2 сместится на расстояние 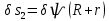 , а шестеренка 2 повернется вокруг точки P (м.ц.с.) на угол , а шестеренка 2 повернется вокруг точки P (м.ц.с.) на угол 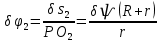 . .Работа момента на этом возможном перемещении системы равна (работа сил тяжести звеньев равна нулю, так как механизм расположен в горизонтальной плоскости и силы тяжести перпендикулярны возможным перемещениям точек их приложения): 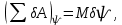 отсюда 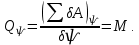 Для определения Q фиксируем координату ѱ (точка O2 становится неподвижной) и даем координате приращение , при этом шестеренка 2 повернется на угол φ2, 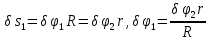 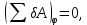 отсюда 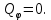 Уравнения Лагранжа второго рода Выберем за обобщенные координаты углы поворота шестерни 1 – и водила O1О2 – ѱ 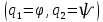 . Тогда из уравнений Лагранжа: . Тогда из уравнений Лагранжа: 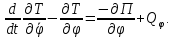 Составим первое дифференциальное уравнение: 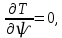 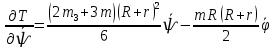 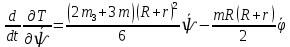 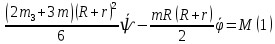 Составляем второе уравнение: 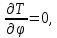 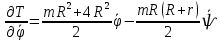 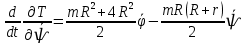 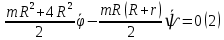 Разрешая уравнения (1) и (2) относительно 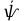 и и 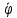 получим: получим: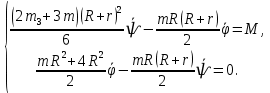 Решаем систему методом подстановки: 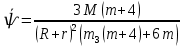 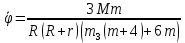 Окончательный ответ: 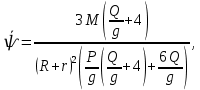 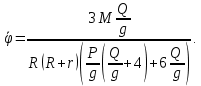 |
